§15. Параллельное и смешанное соединение проводников. — Начало. Основы. — Справочник
§15. Параллельное и смешанное соединение проводников.
Если элементы электрической цепи соединены таким образом, что находятся под одинаковым напряжением, то такое соединение называется параллельным.
Рассмотрим пример по рис. 1. Ток из узла «а» разделяется на четыре ветви, к каждой из которых подключены резисторы. Очевидно, что общее сопротивление уменьшится, если бы был подключен один резистор, а проводимость цепи, наоборот, увеличится. Общая проводимость цепи будет искомая также, как и общее сопротивление при последовательном соединении:
.
Ну а сопротивление будет обратно пропорционально проводимости:
.
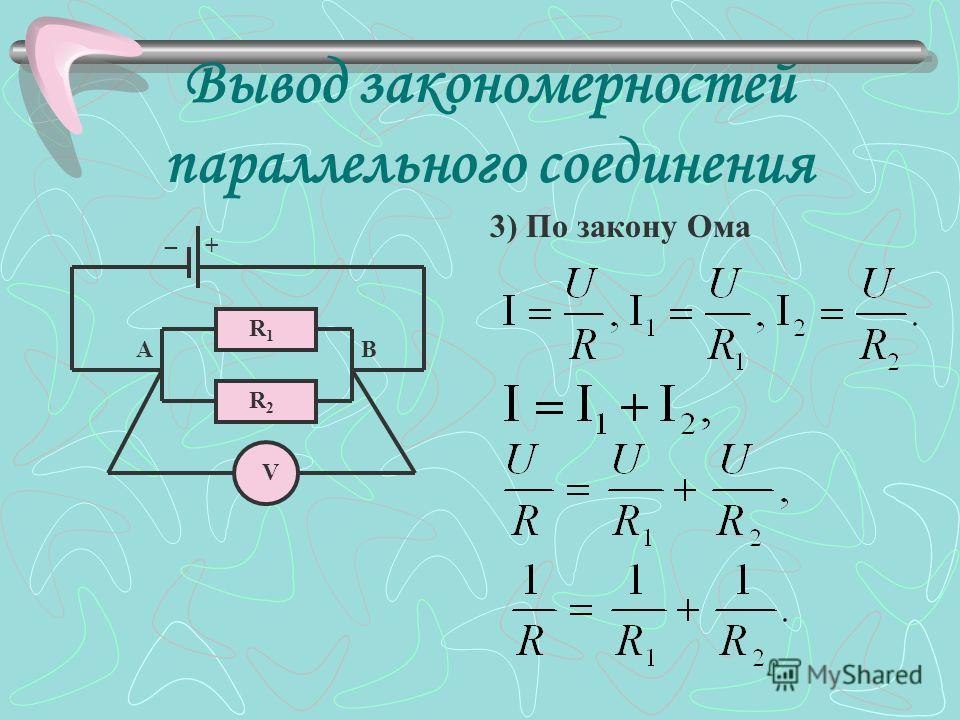
Докажем полученное нами выражение. Обозначим силу тока во входящей цепи буквой I, а силу тока в каждой ветви соответственно I1, I2, I3, I4, а напряжение между сопротивлениями (между точками «а» и «б») – U и общее сопротивление в этих ветвях – R. По закону Ома ток на участке цепи равен:
По закону Ома ток на участке цепи равен:
,
токи в ветвях будут равны соответственно
.
По первому закону Кирхгофа (сумма токов, входящих в общую точку, равна сумме токов, выходящих из этой точки)
I=I1+I2+I3+I4 или что одно и тоже:
Преобразовав обе стороны выражения, получаем:
Собственно, что и требовалось доказать.
Это выражение применимо для любого количества сопротивлений, соединенных параллельно. Если в цепи присутствуют только два параллельно соединенных резистора (либо другого элемента, имеющего сопротивление), то можно воспользоваться более удобной формулой, преобразовав из выше написанного равенства:
Если при параллельном соединении элементы имеют одинаковые сопротивления, то общее сопротивление цепи можно вычислить по формуле Rобщ=R/n, где n – число элементов на данном участке цепи.
Вернувшись к рис. 1, можно записать следующие выражения:
U=I1·R1; U=I2·R2; U=I3·R3; U=I4·R4.
Заметим, что левые части этих соотношений равны, значит равны и правые их части:
I1·R1= I2·R2= I3·R3= I4·R4.
Отсюда получим следующие выражения:
и т. д.
Из этих выражений видно, что токи обратно пропорциональны этим сопротивлениям. То есть, чем меньше сопротивление параллельно включенного элемента, тем больше ток в этом элементе и наоборот.
При неизменном напряжении между узлами цепи, токи в элементах, вставленных в разрыв между этими узлами, в отличие от последовательного соединения, не зависят один от другого. Потому лампы, двигатели и прочие электроприемники обычно включают параллельно.
Потому лампы, двигатели и прочие электроприемники обычно включают параллельно.
Если в цепь с параллельно включенными сопротивлениями добавить последовательно им еще резистор, то такое соединение называется смешанным. Для вычисления эквивалентного сопротивления при смешанном соединении резисторов, определяют сначала общее сопротивление резисторов, соединенных параллельно либо последовательно, заменив их резистором, равным вычисленному. К примеру, чтобы определить сопротивление между точками «б» и «в» (рис. 2) вначале вычисляют значение общего сопротивления между точками «б» и «в»: а потом суммируют найденное значение с сопротивлением R1:
R=R1+ R2·R3/(R2+R3).
Смешанное соединение проводников — презентация онлайн
Смешанное соединение
проводников
Смешанное соединение
проводников
Электрические цепи, с которыми приходится
иметь дело на практике, обычно состоят не
из одного приемника электрического тока, а
из нескольких различных, которые могут
быть соединены между собой по-разному.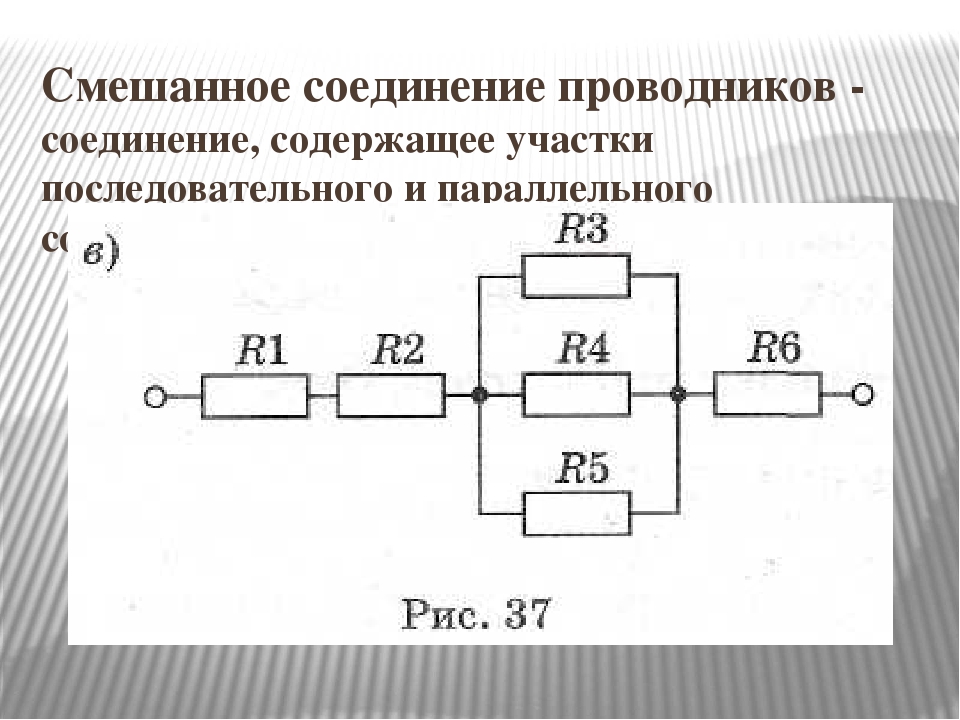
Последовательное соединение
Последовательным
соединением называется
соединение проводников, когда
каждый следующий проводник
включается после предыдущего.
При выходе из строя какогонибудь элемента цепи вся цепь
размыкается.
Основные закономерности
последовательного соединения
1. Сила тока во всех
участках цепи
одинакова.
2. Общее напряжение
равно сумме
напряжений на
отдельных участках
цепи.
3. Общее сопротивление
равно сумме
сопротивлений
отдельных участков
цепи.
Примеры использования
последовательного соединения
Освещение в вагонах
поездов
Лампочки ёлочной
электрической гирлянды
Параллельное соединение
Параллельным соединением
называется такое соединение , при
которым элементы цепи
включаются параллельно друг другу
При выходе из строя какогонибудь элемента параллельного
участка цепи остальная цепь
продолжает работать.
Основные закономерности
параллельного соединения
1.Сила тока в
неразветвленной части
цепи равна сумме сил
токов в каждом участке.
2.Напряжение на
концах всех
параллельно
соединенных
проводников одно и то
же.
3.Величина,равная
обратному значению
общего сопротивления
равна сумме обратных
значений
сопротивлений
параллельных участков
цепи.
Параллельное включение нескольких одинаковых
сопротивлений.
Если в цепь включены N одинаковых
резисторов, то общее сопротивление
определяется по формуле
R = R1/N
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ параллельного
СОЕДИНЕНИЯ
Потребители в быту и
технике удобно
включать параллельно,
так как все они в этом
случае
изготавливаются в
расчете на одинаковое
напряжение. Кроме
того, при выключении
одного потребителя
другие продолжают
действовать.
Смешанное соединение
проводников.
В практике часто применяют смешанное (
последовательное и параллельное) соединение
проводников.
Примеры задач на смешанное
соединение
Самостоятельная работа 18 Смешанное соединение проводников
8 класс ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
Самостоятельная работа 18
Смешанное соединение проводников.
Начальный уровень
1. Начертите схему смешанного соединения проводников. Как можно рассчитать величину его сопротивления?
2. Как соединены между собой электроприборы в вашей квартире? Каковы преимущества именно такого соединения?
3. Три одинаковых сопротивления соединяют различными способами. Начертите схемы этих соединений.
4. Как можно использовать осветительные лампы, рассчитанные на напряжение 110 В, если напряжение в сети равно 220 В? Нарисуйте схему цепи.
5. Как включить два резистора с сопротивлениями 2 Ом и 3 Ом, чтобы их общее сопротивление было минимальным? Максимальным?
6. Увеличится или уменьшится общее сопротивление двух проводников по сравнению с сопротивлением каждого из них, если их включить параллельно? Последовательно?
Увеличится или уменьшится общее сопротивление двух проводников по сравнению с сопротивлением каждого из них, если их включить параллельно? Последовательно?
Средний уровень
1. На рисунке изображена схема соединения проводников,
где R1=3 Ом, R2=6 Ом, R3= 4 Ом. Найти сопротивление всей цепи.
2. Проводники с сопротивлениями R1=2 Ом, R2=3 Ом, R3= 5 Ом соединены по схеме, изображенной на рисунке.
Найдите сопротивление этой цепи.
3. Чему равно общее сопротивление участка цепи, изображенного
на рисунке, если R1=2 Ом, R2=10 Ом, R3= 15 Ом, R4=1 Ом?
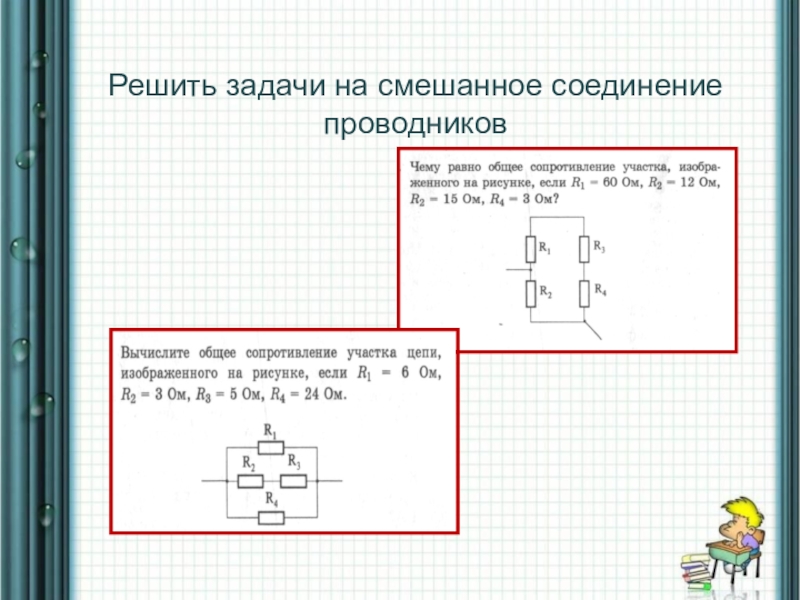
4. Вычислите общее сопротивление участка цепи, изображенного на рисунке, если R1=6 Ом, R2=3 Ом,
R3=5 Ом, R4=24 Ом.
5. Чему равно общее сопротивление участка, изображенного
на рисунке, если R1=60 Ом, R2=12 Ом, R3=15 Ом, R4=3 Ом?
6. Четыре сопротивления R1=1 Ом, R2=2 Ом, R3=3 Ом, R4=4 Ом единены по схеме, изображенной на рисунке.
Четыре сопротивления R1=1 Ом, R2=2 Ом, R3=3 Ом, R4=4 Ом единены по схеме, изображенной на рисунке.
Определите общее сопротивление цепи.
Достаточный уровень
1. Определите сопротивление участка цепи, изображенного на рисунке, между точками С и D, если R1=2 Ом,
R2=5 Ом, R3=20 Ом, R4=5 Ом, R5=10 Ом.
2. Найдите полное сопротивление R показанной на рисунке цепи,
если R1=R2=R5=R6=3 Ом, R4=24 Ом, R3=20 Ом.
3. Определите сопротивление участка АВ,
если R = 1 Ом.
4. Вычислите сопротивление цепи, представленной на рисунке, если сопротивление каждого из резисторов
равно 1 Ом.
5. Вычислите сопротивление цепи, представленной на рисунке,
если R = 1 Ом.
6. Определите общее сопротивление цепи, изображенной на рисунке, если R1=1/2 Ом,
R2= 3/2 Ом, R3=R4=R6=1 Ом, R5=2/3 Ом.
7. Найти сопротивление цепи, изображенной на рисунке,
если каждое из сопротивлений равно 2 Ом.
8. Найти сопротивление участка электрической цепи, если R1=R2=0,5 Ом, R3=8 Ом, R4=12 Ом,
R5=R6=1 Ом, R7=2 Ом, R8=15 Ом, R9=10 Ом, R10=20 Ом.
9. Найти сопротивление R участка цепи между точками А и В,
если R1=R5=R8=12 Ом, R2=R6=R7=6 Ом, R3=3 Ом, R4=24 Ом.
10. Найдите сопротивление цепи, показанной на рисунке. Сопротивление каждого резистора
R, сопротивлением соединительных проводов можно пренебречь.
Высокий уровень
1. Найдите общее сопротивление цепи, показанной на рисунке. Сопротивление каждого
резистора R, сопротивлением соединительных проводов можно пренебречь.
2. Определить общее сопротивление контура,
составленного из одинаковых резисторов r.
3. Найти сопротивление R цепи между точками А и В, если сопротивление каждого звена r.
4. Найти сопротивление R цепи между точками А и В, если сопротивление каждого звена r.
5. Найти сопротивление R цепи между точками А и В, если сопротивление каждого звена r.
6. Найти сопротивление R цепи между точками А и В, если сопротивление каждого звена r .
7. Найти сопротивление R цепи между точками А и В, если сопротивление каждого звена r.
8. Из 12 одинаковых сопротивлений спаян куб. Найдите сопротивление
этого каркаса при включении его в цепь вершинами А и В.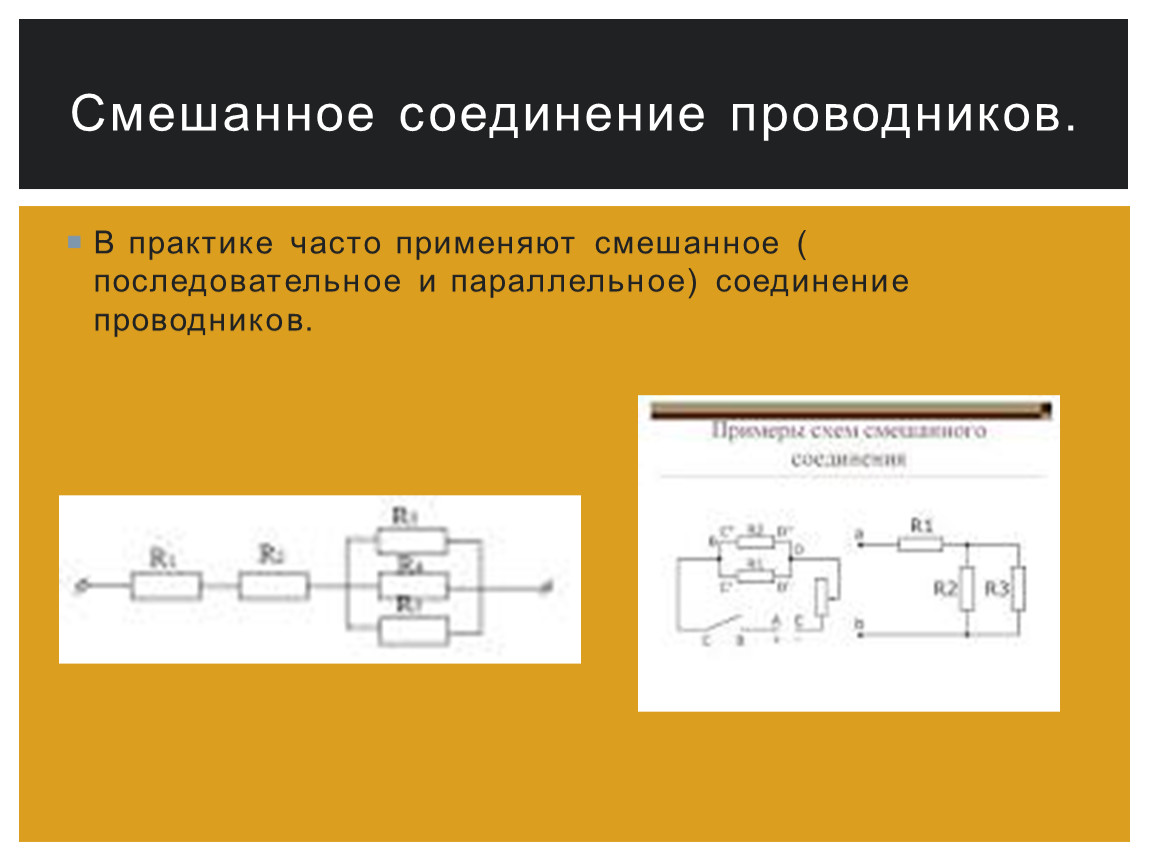
6. Смешанное соединение проводников |
Отгадайте загадку: «По тропинкам Для решения задач на эту тему необходимо понимать, как течет ток 06 Последовательное и параллельное соединение резисторов
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно) На рисунке 1 показан простейший пример смешанного соединения резисторов. На этом рисунке видно, что резисторы R2, R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно. Алгоритм решения: Пример расчета участка цепи со смешанным соединением резисторов приведен на рис 2. Интерактивное изложение материала по теме «Смешанное соединение проводников Интерактивная |
Updating…
Ольга Федотова,
5 янв. 2016 г. , 09:32
, 09:32
Ольга Федотова,
5 янв. 2016 г., 09:33
ć
Ольга Федотова,
5 янв. 2016 г., 09:33
ĉ
Ольга Федотова,
5 янв. 2016 г., 09:33
ĉ
Ольга Федотова,
5 янв. 2016 г., 09:38
ć
Ольга Федотова,
5 янв. 2016 г., 09:33
Ольга Федотова,
5 янв. 2016 г., 09:33
Ольга Федотова,
5 янв. 2016 г., 09:33
Ольга Федотова,
5 янв. 2016 г., 09:33
Ольга Федотова,
5 янв. 2016 г., 09:33
ĉ
Ольга Федотова,
5 янв. 2016 г., 09:39
4 цепи cepi.rar
(635k)
Ольга Федотова,
5 янв. 2016 г., 09:33
Ċ
Ольга Федотова,
28 февр. 2016 г., 21:15
Ольга Федотова,
5 янв. 2016 г., 00:08
Свойства и основные правила смешанного соединения
Свойства и основные правила смешанного соединения.
Когда речь заходит о смешанном соединении, то, судя по одному только названию не сложно догадаться, что электрическая принципиальная схема данного соединения состоит из некой совокупности параллельно и последовательно включенных проводников (допускаются абсолютно любые комбинации).
Единственным нюансом является то, что в состав данных соединений входят как отдельные резисторы, так и более сложные комбинации (составные участки).
При расчете смешанного соединения следует опираться на ранее изученные свойства параллельного и последовательного соединения, так как, что-то новое придумать вряд ли удастся. Перед расчетом всех необходимых составляющих нужно очень аккуратно и грамотно расчленить исходную схему на менее сложные участки, так, чтобы в итоге образовались отдельные последовательные и параллельные соединения.
А теперь более подробно рассмотрим пример так называемого смешанного соединения проводников, и сделаем мы это на примере данной электрической принципиальной схемы.
Предположим, что U = 14 В, R1 = 2 Ом, R2 = 3 Ом, R3 = 3 Ом, R4 = 5 Ом, R5 = 2 Ом.С помощью этих формул не сложно будет определить ток, который протекает в электрической цепи и соответственно через каждый из ранее представленных резисторов.
При этом не стоит забывать о том, что нашей первоначальной целью является расчет всей элементной базы. А если учесть то, что данная цепь состоит сразу из двух последовательно соединенных друг с другом участков bс и аb, то сопротивление на участке аb можно будут описать следующим образом:
А если учесть то, что данная цепь состоит сразу из двух последовательно соединенных друг с другом участков bс и аb, то сопротивление на участке аb можно будут описать следующим образом:
Кроме этого, участок bс, сам по себе является в данной схеме параллельным соединением, так как состоит из двух последовательно включенных резисторов, а именно резистора и . Они в свою очередь параллельно подключены к пятому резистору . Опираясь на ранее описанные правила и свойства сопротивление на участке цепи аb можно описать с помощью следующей формулы.Соответственно результирующее сопротивление цепи будет представлено в виде следующего выражения:
После произведенных расчетов не сложно определить силу тока, которая определяется с помощью следующего равенства:Для того чтобы вычислить ток в цепи, и непосредственно в каждом резисторе производим расчет сразу на обоих участках:В процессе расчетов следует обратить особое внимание на то, что в итоге сумма всех указанных напряжений должна быть равной 14 В.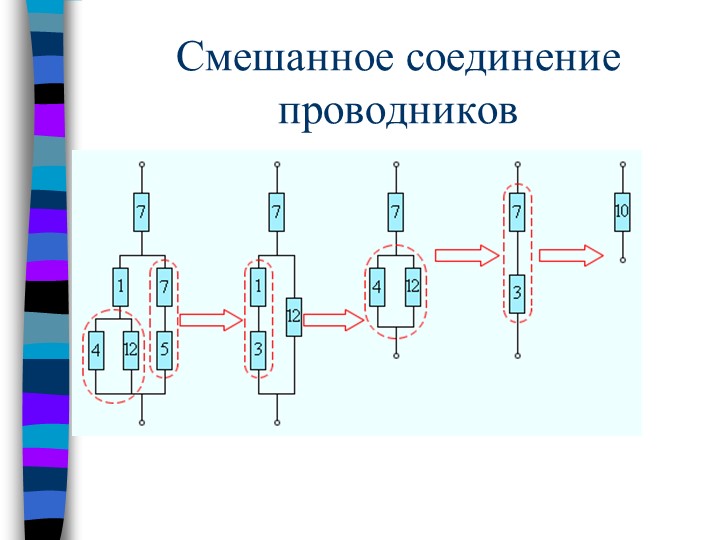
Или же соответствовать общему напряжению в цеп (исходя из правила предусмотренного для последовательного соединения).
Предположим, что в момент напряжения резистор , точно также как и резистор , на участке аb находится под напряжением , поэтому справедливыми будут следующие выражения:А это значит, что и в сумме дают нам 5 А, (так как в принципе и должно быть при параллельном соединении).
Результирующая сила тока, которая проходит через резисторы и в итоге окажется одинаковой, из-за того, что резисторы между собой соединены последовательно. Для большей наглядности данного примера приведем следующую формулу:Стало быть, в электрической цепи, через последний, пятый резистор протекает ток А.
Дата: Среда, 08 Августа 2018
Последовательное и параллельное соединение
В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:
- ток;
- напряжение;
- сопротивление.

В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.
Последовательное соединение
Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.
При последовательном соединении:
- сила тока во всех проводниках одинакова;
- напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
- сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Пример 1
Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.
Решение
Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.
1. Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A
2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:
Uл1=Uл2 = Iн*R = 0,9*122 = 110 B
Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.
Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.
Пример 2
Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.
Решение
1. Определяем ток протекающей по участкам цепи:
Определяем ток протекающей по участкам цепи:
Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A
2. Определяем напряжение на каждой из ламп накаливания:
Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B
Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.
Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.
Параллельное соединение
Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.
Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.
При параллельном соединении:
- напряжение на всех проводниках одинаково;
- сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
- величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Пример 3
Определить токи и напряжения всех участков цепи (рис.5), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
- Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.5.
1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:
2. Определяем сопротивление всей цепи [Л1, с.47]:
3. Определяем силу тока цепи по закону Ома:
4. Определяем токи для каждой цепи [Л1, с.47]:
5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:
Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)
Смешанное соединение
Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.
Пример 4
Определить токи и напряжения всех участков цепи (рис.7), если известно:
- Номинальное напряжение сети Uн = 220В;
- Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
- Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
- Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
Сопротивление цепи ВС составляет Rвс = 43,668 Ом.
Решение
Составляем схему замещения для схемы, представленной на рис.7.
1. Определяем сопротивление всей цепи:
Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом
2. Определяем силу тока цепи, согласно закона Ома:
3. Определяем напряжение на первом сопротивлении:
Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B
4. Определяем напряжение на участке ВС:
Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B
5. Определяем токи для каждой цепи участка ВС:
6. Выполним проверку для участка цепи ВС:
Выполним проверку для участка цепи ВС:
Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)
Литература:
- Общая электротехника с основами электроники, В.С. Попов, 1972 г.
- Справочная книга электрика. В.И. Григорьева. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Последовательное соединение схема формула. Последовательное и параллельное соединение
Содержание:
Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений.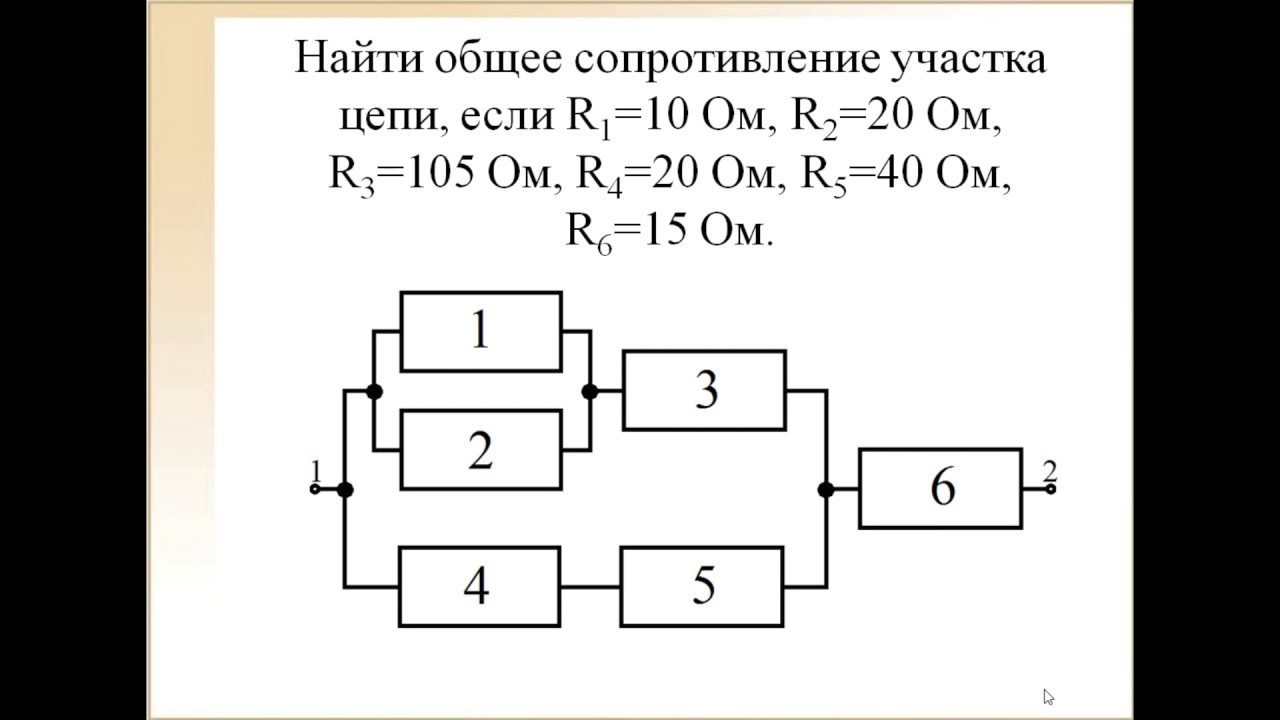 Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин.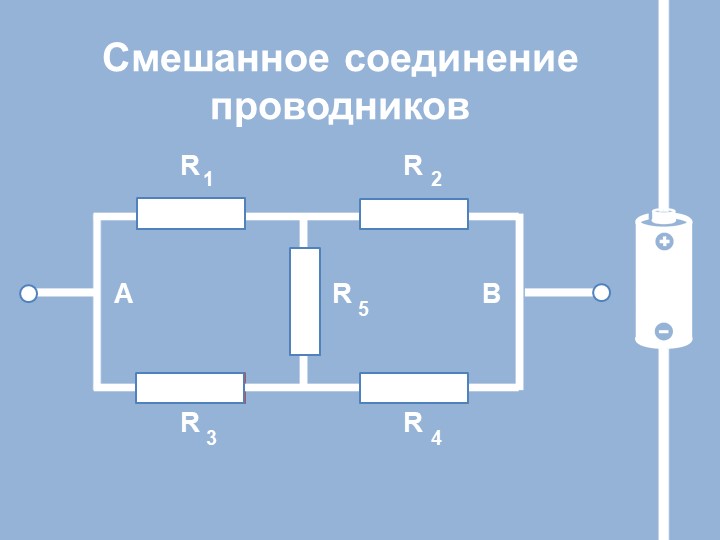 Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Содержание:
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.

- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи.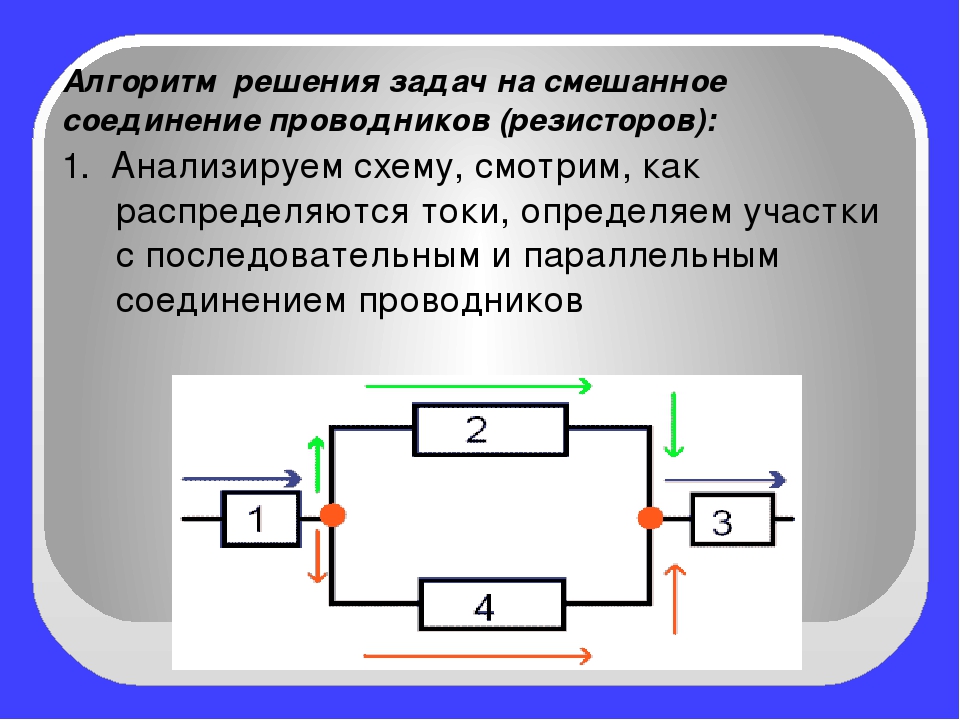 Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.

- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R
. Этот закон, установленный экспериментально, называется закон Ома
Этот закон, установленный экспериментально, называется закон Ома
(для участка цепи).
Закон Ома
для участка цепи
: сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника.
Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д
ва основных типа соединения проводников
: последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводников
При последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова:
I 1 =
I 2 =
I
.
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений
: R 1 + R 2 = R
. Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 =
I*
R 1
, U 2 = I*R 2
. В таком случае общее напряжение равно U = I (
R 1 +
R 2)
. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике
: U = U 1 + U 2
.
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы
:
1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводников
Примером параллельного соединения
проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U
В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U
.
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I =
I 1 +
I 2
.
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2
. Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2
, U = U 1 = U 2
,
1/R = 1/R 1 + 1/R
2
Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г
, то их общее сопротивление равно: R = г/2
. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:
1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор.
 В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины. - Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном. Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Mixed Conductor — обзор
Multiphase Composites
На раннем этапе исследований была предложена концепция матрицы со смешанной проводимостью, в которой мелкие частицы фазы реагента были равномерно диспергированы в твердой металлической матрице со смешанной проводимостью. Такая композитная структура электрода может улучшить кинетику межфазной реакции и достичь истинной микроструктурной обратимости. Например, фаза реагента, такая как кремний или кадмий, тонко диспергирована в матрице Li 13 Sn 5 , и цикличность регулируется в диапазоне потенциалов, в котором Li 13 Sn 5 не вступает в реакцию.Инертная матрица Li 13 Sn 5 не только обеспечивает быстрый канал транспортировки Li + для электроактивных доменов, но также обеспечивает морфологическую стабильность электрода. Таким образом достигается хорошая производительность при езде на велосипеде. Строгие требования к контролю напряжения разряда и низкая удельная плотность заряда, связанная с высоким содержанием инертной матрицы, ограничивают практическое применение электродных систем этого типа. Другой подход — использовать структуры многофазных сплавов с различной реакционной способностью по отношению к литию.Электроосажденные пленки Sn, SnSb x , SnAg x и SnCu x были исследованы в качестве вводимых электродов.
Такая композитная структура электрода может улучшить кинетику межфазной реакции и достичь истинной микроструктурной обратимости. Например, фаза реагента, такая как кремний или кадмий, тонко диспергирована в матрице Li 13 Sn 5 , и цикличность регулируется в диапазоне потенциалов, в котором Li 13 Sn 5 не вступает в реакцию.Инертная матрица Li 13 Sn 5 не только обеспечивает быстрый канал транспортировки Li + для электроактивных доменов, но также обеспечивает морфологическую стабильность электрода. Таким образом достигается хорошая производительность при езде на велосипеде. Строгие требования к контролю напряжения разряда и низкая удельная плотность заряда, связанная с высоким содержанием инертной матрицы, ограничивают практическое применение электродных систем этого типа. Другой подход — использовать структуры многофазных сплавов с различной реакционной способностью по отношению к литию.Электроосажденные пленки Sn, SnSb x , SnAg x и SnCu x были исследованы в качестве вводимых электродов. Экспериментальные результаты показывают, что уменьшение размера зерна и использование микроструктурированных многофазных матриц может значительно повысить стабильность циклирования. Поскольку каждая фаза в многофазной структуре имеет разную реакционную способность по отношению к литию, введение лития в многофазную матрицу осуществляется в пошаговом режиме. Менее активные или неактивные фазы могут сдерживать расширение активных доменов.Фактически, легкоплавкие сплавы свинца, олова, висмута и кадмия (представленные металлом Вуда) использовались в качестве отрицательного электрода в коммерческих батареях кнопочного типа, разработанных Мастушитой в 1980-х годах. Однако следует признать, что многоплатный характер электродного потенциала, связанный с многофазными материалами, не является благоприятным для практического применения. Может быть допустима только небольшая разность потенциалов между многофазными композициями. Кроме того, микроструктурированные сплавы, состоящие из целых активных фаз, все же быстро теряют емкость при желаемой глубине заряда.
Экспериментальные результаты показывают, что уменьшение размера зерна и использование микроструктурированных многофазных матриц может значительно повысить стабильность циклирования. Поскольку каждая фаза в многофазной структуре имеет разную реакционную способность по отношению к литию, введение лития в многофазную матрицу осуществляется в пошаговом режиме. Менее активные или неактивные фазы могут сдерживать расширение активных доменов.Фактически, легкоплавкие сплавы свинца, олова, висмута и кадмия (представленные металлом Вуда) использовались в качестве отрицательного электрода в коммерческих батареях кнопочного типа, разработанных Мастушитой в 1980-х годах. Однако следует признать, что многоплатный характер электродного потенциала, связанный с многофазными материалами, не является благоприятным для практического применения. Может быть допустима только небольшая разность потенциалов между многофазными композициями. Кроме того, микроструктурированные сплавы, состоящие из целых активных фаз, все же быстро теряют емкость при желаемой глубине заряда.
В 1997 году Fuji Photo Film Celltec Co. анонсировала новую литий-ионную технологию (STALION) с использованием ATCO в качестве отрицательных электродов. Композит с номинальным составом SnB 0,56 P 0,4 Al 0,42 O 3,6 в качестве примера синтезирован по технологии плавления из SnO, B 2 O 3 , Sn 2 P 2 O 7 , Al 2 O 3 и другие добавки. Электрод ATCO реагирует с литием примерно при 0.5 В по сравнению с Li / Li + и демонстрирует большую удельную емкость около 600 мАч g -1 (или 2200 мАч см -3 ). Механизм электродной реакции включает необратимое восстановление окисленного олова в композите до металлического олова во время первого процесса зарядки с последующим обратимым легированием и удалением сплава. Тонкое распределение аморфного олова в матрице оксида B – P – Al стабилизирует микроструктуру композита, что приводит к заметному увеличению срока службы. Однако экспериментальные результаты композиционных оксидов олова, относящиеся к ATCO, показывают, что постепенная агрегация доменов олова может происходить во время цикла, если отсечка напряжения не контролируется.Агрегация олова неблагоприятна для долгосрочной циклируемости. Более того, первоначальное необратимое снижение приводит к большой потере емкости и должно быть компенсировано избытком литийсодержащего материала положительного электрода. В результате плотность энергии ячейки будет заметно уменьшена. Это основная причина того, что ячейка STALION не поступила в продажу. Чтобы избежать необратимого восстановления металлических соединений, были исследованы композиционные материалы из сплава, такие как Sn – Fe (–C). В композите Sn – Fe (–C) активная фаза Sn 2 Fe тонко диспергирована в совместимой матрице SnFe 3 C со смешанной проводимостью.SnFe 3 C реагирует с очень небольшим количеством лития и может рассматриваться как неактивная фаза. Связующая линия, соединяющая Sn 2 Fe с SnFe 3 C на тройной фазовой диаграмме Sn – Fe – C, полезна для производства однородных и контролируемых активной / неактивной фаз композитов с помощью технологии шаровой мельницы.
Однако экспериментальные результаты композиционных оксидов олова, относящиеся к ATCO, показывают, что постепенная агрегация доменов олова может происходить во время цикла, если отсечка напряжения не контролируется.Агрегация олова неблагоприятна для долгосрочной циклируемости. Более того, первоначальное необратимое снижение приводит к большой потере емкости и должно быть компенсировано избытком литийсодержащего материала положительного электрода. В результате плотность энергии ячейки будет заметно уменьшена. Это основная причина того, что ячейка STALION не поступила в продажу. Чтобы избежать необратимого восстановления металлических соединений, были исследованы композиционные материалы из сплава, такие как Sn – Fe (–C). В композите Sn – Fe (–C) активная фаза Sn 2 Fe тонко диспергирована в совместимой матрице SnFe 3 C со смешанной проводимостью.SnFe 3 C реагирует с очень небольшим количеством лития и может рассматриваться как неактивная фаза. Связующая линия, соединяющая Sn 2 Fe с SnFe 3 C на тройной фазовой диаграмме Sn – Fe – C, полезна для производства однородных и контролируемых активной / неактивной фаз композитов с помощью технологии шаровой мельницы. Тонкая дисперсия наноразмерного Sn 2 Fe в SnFe 3 C буферизует изменение объема активной фазы и предотвращает агрегацию мелких частиц железа. Таким образом, эффективность езды на велосипеде может быть заметно улучшена.
Тонкая дисперсия наноразмерного Sn 2 Fe в SnFe 3 C буферизует изменение объема активной фазы и предотвращает агрегацию мелких частиц железа. Таким образом, эффективность езды на велосипеде может быть заметно улучшена.
Постепенно стало ясно, что полезные структуры сплава, способные полностью подавить объемный эффект, могут быть получены путем максимально однородного диспергирования активных доменов в структурно-стабильной матрице, как показано на Рисунке 8. Тем не менее, агрегирование Наноразмерные активные частицы, вызываемые реакцией электрохимического легирования, обычны не только для пластичных олова и интерметаллидов олова, но и для твердого кремния. Следовательно, соответствующая буферная матрица должна быть способна приспособиться к расширению реагентов, предотвратить агрегацию активных нанодоменов и обеспечить электрический путь.Для этого в качестве диспергирующих фаз использовали проводящие нитриды и силициды переходных металлов. Исследователи из Matsurhita Battery Industrial сообщили, что кристаллическое состояние активной кремниевой фазы сильно влияет на циклируемость двухфазного композиционного материала TiSi 2 –Si, полученного механическим легированием. По сравнению с фазой кристаллического кремния размером 20 нм, a-Si в композите продемонстрировал заметное улучшение сохранения удельной емкости примерно при 700 мАч g -1 .В другом случае внутричастичные поры размером ~ 200 нм были введены в композит NiSi – Si путем растворения непрореагировавшего никеля. Этот композитный электрод показал значительно меньшее расширение толщины и скорость ослабления емкости при электрохимическом циклировании по сравнению с электродом из чистых кремниевых частиц. Композит, состоящий из 76 мас.% NiSi и 24 мас.% Кремния, давал начальную удельную вводимую емкость лития 1250 мАч g -1 и эффективность заряда и разряда около 87%. После второго цикла КПД вырос до более чем 99%.Следует отметить, что доступная емкость силицидов переходных металлов значительно варьируется от литературы к литературе. Чистота фазы, микроструктура и условия зарядки могут иметь большое влияние на практическую емкость.
По сравнению с фазой кристаллического кремния размером 20 нм, a-Si в композите продемонстрировал заметное улучшение сохранения удельной емкости примерно при 700 мАч g -1 .В другом случае внутричастичные поры размером ~ 200 нм были введены в композит NiSi – Si путем растворения непрореагировавшего никеля. Этот композитный электрод показал значительно меньшее расширение толщины и скорость ослабления емкости при электрохимическом циклировании по сравнению с электродом из чистых кремниевых частиц. Композит, состоящий из 76 мас.% NiSi и 24 мас.% Кремния, давал начальную удельную вводимую емкость лития 1250 мАч g -1 и эффективность заряда и разряда около 87%. После второго цикла КПД вырос до более чем 99%.Следует отметить, что доступная емкость силицидов переходных металлов значительно варьируется от литературы к литературе. Чистота фазы, микроструктура и условия зарядки могут иметь большое влияние на практическую емкость.
Рисунок 8. Схематическая структура легированных композиционных электродных материалов.
Возможным способом получения нанодисперсных композитных электродных материалов является прямое восстановление монооксида кремния (SiO) или соединений олова восстановительными металлами, такими как алюминий, магний и литий, при высокоэнергетическом механическом измельчении.Из-за плохой проводимости кремниевых и оксидных диспергирующих фаз, образующихся in situ, часто вводится углерод. Для восстановления SiO с использованием лития в качестве восстановителя с помощью просвечивающей электронной микроскопии высокого разрешения (HRTEM) в сочетании с дифракцией электронов на выбранной площади было обнаружено, что наноразмерные зерна кремния (<10 нм) были равномерно диспергированы в матрице, состоящей из ортосиликата лития (Li 4 SiO 4 ) нанозерна и другие аморфные компоненты. Этот композитный электрод показывает хорошие электрохимические характеристики при низкой скорости заряда и разряда (<0.4 С ). Стабильная удельная емкость выше 700 мАч g -1 может поддерживаться до 50 циклов. В таблице 2 приведены приблизительные электрохимические данные для вышеупомянутых сплавов композитных электродных материалов.
В таблице 2 приведены приблизительные электрохимические данные для вышеупомянутых сплавов композитных электродных материалов.
Таблица 2. Сравнение характеристик нескольких композитов Sn и Si
| Материал отрицательного электрода | КПД 1-го цикла (%) | Удельная разрядная емкость 1-го цикла (мАч г −1 ) | Удельная емкость удерживание мАч г -1 (цикл №) | |
|---|---|---|---|---|
| Композитный ATCO | 63 | 650 | 585 (100) | |
| Композит Sn – Fe – C | 79 | 285 | 170 (80) | Si3 / |
| — | 710 | 670 (70) | ||
| Si / NiSi | 87 | 1088 | 550 (50) | |
| Si / Al 2 O O | 79 | 650 | 560 (40) | |
| Si / Li 4 SiO 4 / графит | 81 | 770 | 762 (50) |
олово аморфное окись.
PHYSICS_10_19_V2_TG_ Закон Ома для смешанного соединения проводников.
Обзор. Завершите предложения (попарно)
В
параллельной цепи, могут быть изложены некоторые общие правила в отношении
величины напряжения, тока, сопротивления и мощности. Выразите эти правила,
своими словами:
ответы
«В последовательной цепи добавляемое напряжение, равное
итого »
«В последовательной цепи ток равен
все компоненты »
«В последовательной цепи сопротивление добавляется к
равняется общей сумме »
«В параллельной цепи напряжение на всех
компоненты.”
«В параллельной цепи токи в сумме равны
Всего.»
«В параллельной цепи сопротивления уменьшаются до
Общая.»
Деятельность
Определите, какая из этих цепей
параллельная цепь (может быть показано несколько!):
Цепи D и E — это параллельных цепей .
Примечания:
Цель этого вопроса — получить
студенты, чтобы определить, какая отличительная характеристика однозначно определяет
цепь как «параллельная.»После того, как это было идентифицировано, есть несколько
выводы, которые могут быть сделаны (относительно падений напряжения, токов,
сопротивления и т. д.).
У некоторых студентов могут быть трудности
различая, что цепь E является параллельной цепью, но она
является!
(З) Работа всего класса. Использование
Закон Ома для смешанного соединения проводников
Помните правила для тока и напряжения
в последовательной и параллельной цепях
(G) Групповая работа.Рабочий лист: схемы
& Закон Ома
Для дальнейшей практики анализа комбинации
схем, рассмотрите возможность анализа проблем в этом действии .
Для способных студентов (Дифференциация)
Проведите соединительные провода на этом
клеммную колодку так, чтобы три лампочки были подключены параллельно каждой
прочее и с аккумулятором.
Примечания:
Одна из самых сложных визуализаций
задачами для начинающих студентов электроники перевод принципиальных схем на
физические макеты и наоборот.К сожалению, это умение, которого я не вижу
подчеркивается почти достаточно в большинстве основных учебных программ по электронике. Кажется,
большая часть учебного времени тратится на математический анализ бесполезного резистора
сетей, и недостаточно времени тратится на построение пространственных отношений учащихся
навыки и умения.
В то время как последовательные соединения очень просты
визуализировать на клеммных колодках, параллельные соединения сложнее. Работа
с вашими учениками через этот вопрос, помогая тем, у кого нет врожденных
пространственные отношения способность быстро увидеть решение.
«Уловка», которую я часто использую, чтобы помочь студентам
Чтобы развить этот навык, нужно попросить их сначала нарисовать красивую чистую схематическую диаграмму.
Затем они обводят каждый провод на схеме, когда рисуют его на картинке.
диаграмма. Таким образом, они не упускают из виду соединения в
графическая схема.
Схема, показанная здесь, обычно
именуется делителем тока . Рассчитайте падение напряжения
на каждом резисторе, ток, потребляемый каждым резистором, и общая сумма
электрического сопротивления ßen »от 9-вольтовой батареи:
• Ток через 2 кОм
резистор =
• Ток через 3 кОм
резистор =
• Ток через 5 кОм
резистор =
• Напряжение на каждом резисторе =
• рупий всего =
Можете ли вы придумать какой-нибудь практический
приложения для такой схемы?
Ответ
• Ток через 2 кОм
резистор = 4.5 мА
• Ток через 3 кОм
резистор = 3 мА
• Ток через 5 кОм
резистор = 1,8 мА
• Напряжение на каждом резисторе = 9 В
• Всего рэнд = 967,74
Ом
Сколько тока потребляется от
аккумулятор в этой цепи? Как эта цифра соотносится с отдельным резистором
токам, а к общему значению сопротивления?
Примечания:
Некоторым учащимся трудно понять диаграмму.
следовать, и поэтому они обнаружат, что задача анализа помогает рисовать
эквивалентная принципиальная схема для этой цепи со всеми клеммами
помечены.Я рекомендую вам не предлагать это решение сразу, а
предложите своим ученикам самостоятельно придумать методы решения проблем.
Конечно, кто-то в классе подумал об этом, и влияние
такое предложение, исходящее от сверстника, сильнее, чем если бы оно исходило от вас,
инструктор.
Обязательно задайте своим ученикам этот вопрос:
«Почему этот тип схемы обычно называют делителем тока ?»
(f) Формирующее оценивание.Решение проблемы
1. Если через ячейку протекает ток
составляет 2 А, а все резисторы омические, рассчитать напряжение на ячейке
и каждый из резисторов R 1 , R 2 и R 3 соответственно.
Ответ
Чтобы найти напряжение, нам сначала нужно найти
эквивалентное сопротивление. Начнем с вычисления эквивалентного сопротивления
параллельная комбинация:
1 / Rp = 1 / R 2 + 1 / R 3 = 1/2 + 1/4 = 3/4 = 1,33 Ом
R p = 1,33 Ом
Теперь у нас есть схема с двумя резисторами.
последовательно, чтобы мы могли рассчитать эквивалентное сопротивление:
Rs = R 1 + Rp = 4,66 + 1,33 = 5,99 Ом
Значит, напряжение на ячейке:
В = I⋅R = (2) (5,99) = 12 В
Ток через параллель
комбинация резисторов 2 А.(Сила тока одинакова для серийных комбинаций
резисторов, и мы можем рассматривать весь параллельный набор резисторов как один
последовательный резистор.)
Используя это, мы можем найти напряжение через
каждый из резисторов. Начнем с нахождения напряжения на R 1 :
В = I⋅R = (2) (4,66) = 9,32 В
Теперь находим напряжение на
параллельная комбинация:
В = I⋅R = (2) (1,33) = 2,66 В
Поскольку напряжение на каждом резисторе в
параллельная комбинация такая же, это также напряжение на
резисторы R 2 и R 3 .
2. Заполните таблицу
значения для этой схемы:
Ответ
Примечания:
Обсудите со своими учениками, что
процедура может быть для вычисления неизвестных значений в этой задаче, а также
как они могут проверить свою работу.
3. Изучите схему ниже:
Если разность потенциалов на
ячейка 12В,
рассчитать:
·
ток I через ячейку.
Чтобы найти ток I, нам сначала нужно
найти эквивалентное сопротивление. Начнем с вычисления эквивалента
сопротивление параллельной комбинации:
1/ р = 1/ 1 + 1/ 2 + 1/ 3 = 1/3 + 1/5 + 1/1 = 23/15
R p = 0,652 Ом
Теперь у нас есть схема с двумя резисторами.
последовательно, чтобы мы могли рассчитать эквивалентное сопротивление:
рупий = 4 + рупий = 2 + 0,652 = 2,652
Ом
Значит, ток через ячейку:
I = V / R = 122,652 = 4,52 А ток через
резистор 5 Ом.
Ответ
Ток через параллель
комбинация резисторов составляет 4,52 А. (Ток такой же через последовательные комбинации
резисторов, и мы можем рассматривать весь параллельный набор резисторов как один
последовательный резистор. )
)
Используя это, мы можем найти напряжение через
параллельная комбинация резисторов (не забудьте использовать эквивалентную параллельную
сопротивление, а не эквивалентное сопротивление цепи):
В = I⋅R = (4,52) (0,652) = 2,95 В
Поскольку напряжение на каждом резисторе в
параллельная комбинация такая же, это также напряжение на резисторе 5 Ом.
Итак, теперь мы можем рассчитать текущий
через резистор:
I = V / R = 2,955 = 0,59 А
Скачано с
www.znanio.ru
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательного или параллельного соединения.Когда все устройства в цепи соединены последовательным соединением, тогда схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи.В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами. Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи.В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
При анализе комбинированных цепей критически важно иметь твердое представление о концепциях, которые относятся как к последовательным цепям, так и к параллельным цепям. Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы.Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии
R Всего = 1 + 2 R 3 +… | Параллельные схемы
|
Каждое из вышеперечисленных понятий имеет математическое выражение.Объединение математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных схем
Основная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом.Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
После преобразования в последовательную схему анализ можно проводить обычным образом.Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем общее или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …
, где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, подключенных параллельно.Если два или более резистора, находящихся в параллельных ветвях, не имеют равного сопротивления, необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной схеме, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи.Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи.Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , размещенными в параллельных ветвях. Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
рандов до = 1 рандов + 2 рандов + 3 рандов +…
Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах.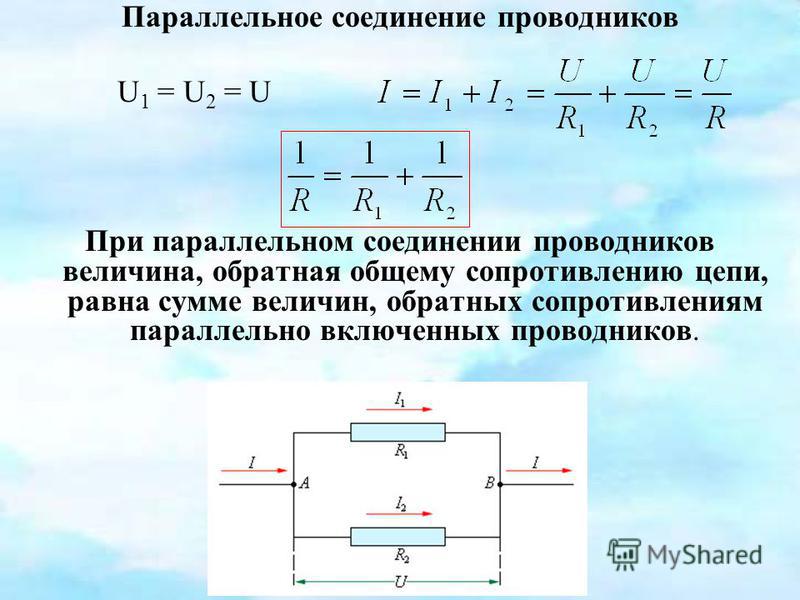 Весь метод проиллюстрирован ниже на двух примерах.
Весь метод проиллюстрирован ниже на двух примерах.
Пример 1:
Первый пример — самый простой — резисторы, включенные параллельно, имеют одинаковое сопротивление.Цель анализа — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 .Таким образом, общее сопротивление составляет
R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 Ом
R до = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.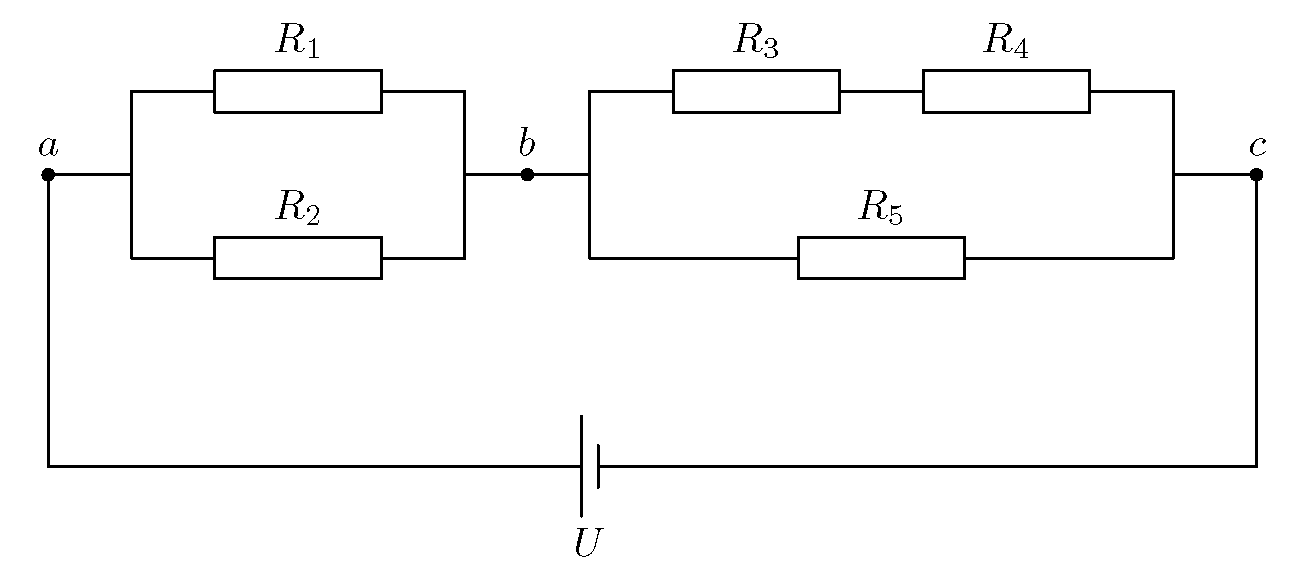 При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (60 В) / (15 Ом)
I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи.При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
I до = I 1 = I 4 = 4 А
Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению.Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 А.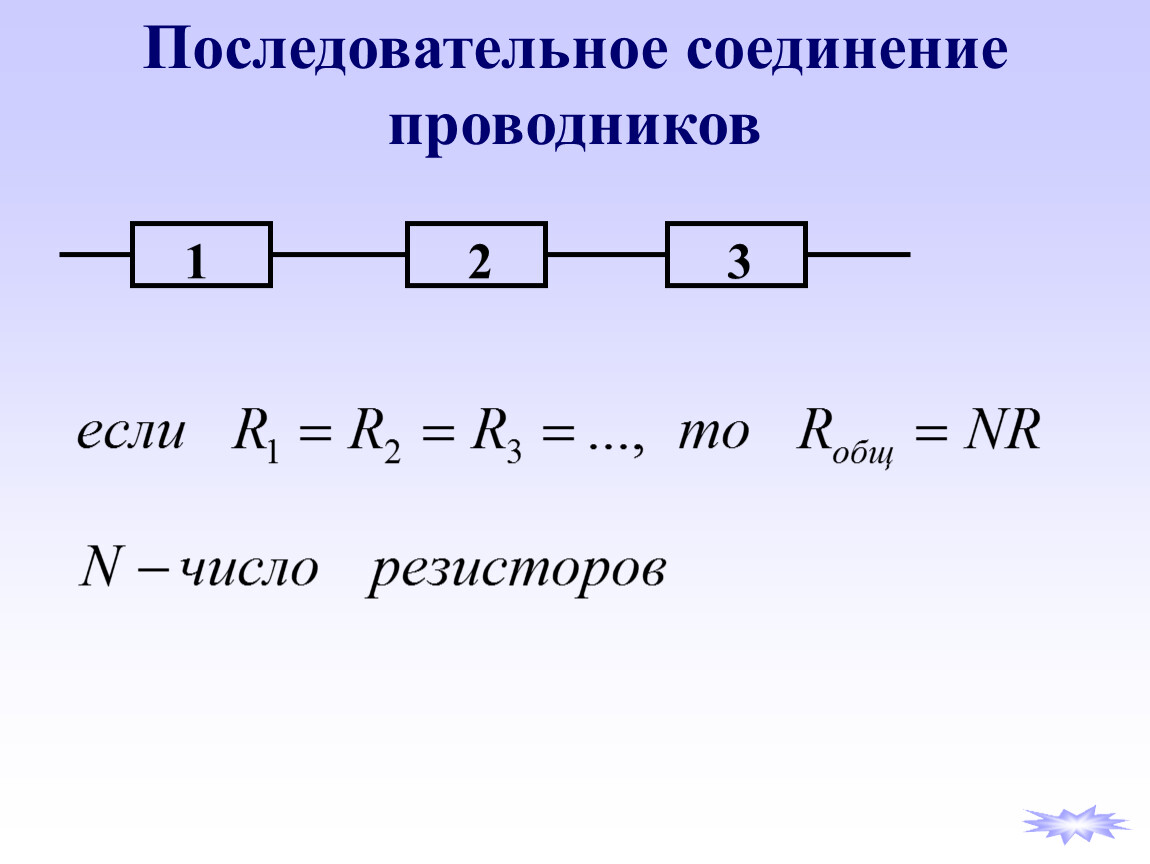
I 2 = I 3 = 2 ампер
Теперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)
ΔV 1 = 20 В
ΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 В
ΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 В
ΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:
Второй пример — более сложный случай — резисторы, включенные параллельно, имеют другое значение сопротивления. Цель анализа та же — определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить, используя обычную формулу для эквивалентного сопротивления параллельных ветвей:
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 …
1 / R экв = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом.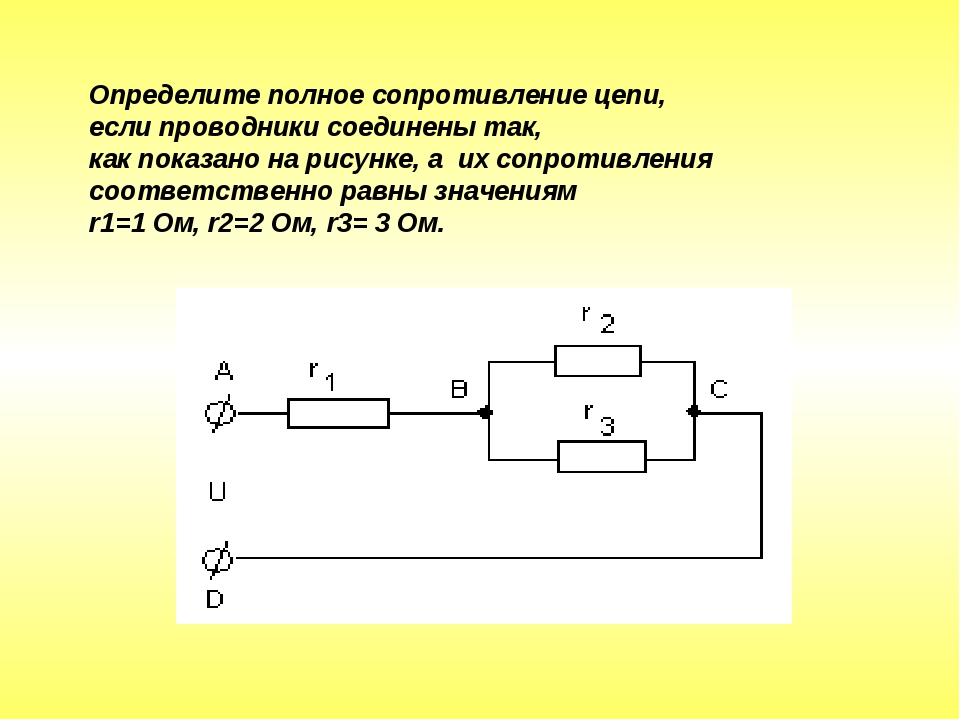 Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
R до = R 1 + 3 Ом + R 4 = 5 Ом + 3 Ом + 8 Ом
R до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I tot = ΔV tot / R tot = (24 В) / (16 Ом)
I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. При этом резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 А
Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ответвлениях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неравный ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ответвлениях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)
ΔV 1 = 7,5 В
ΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и R 4 . Таким образом,
ΔV 2 = V 3 = 4,5 В
Зная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.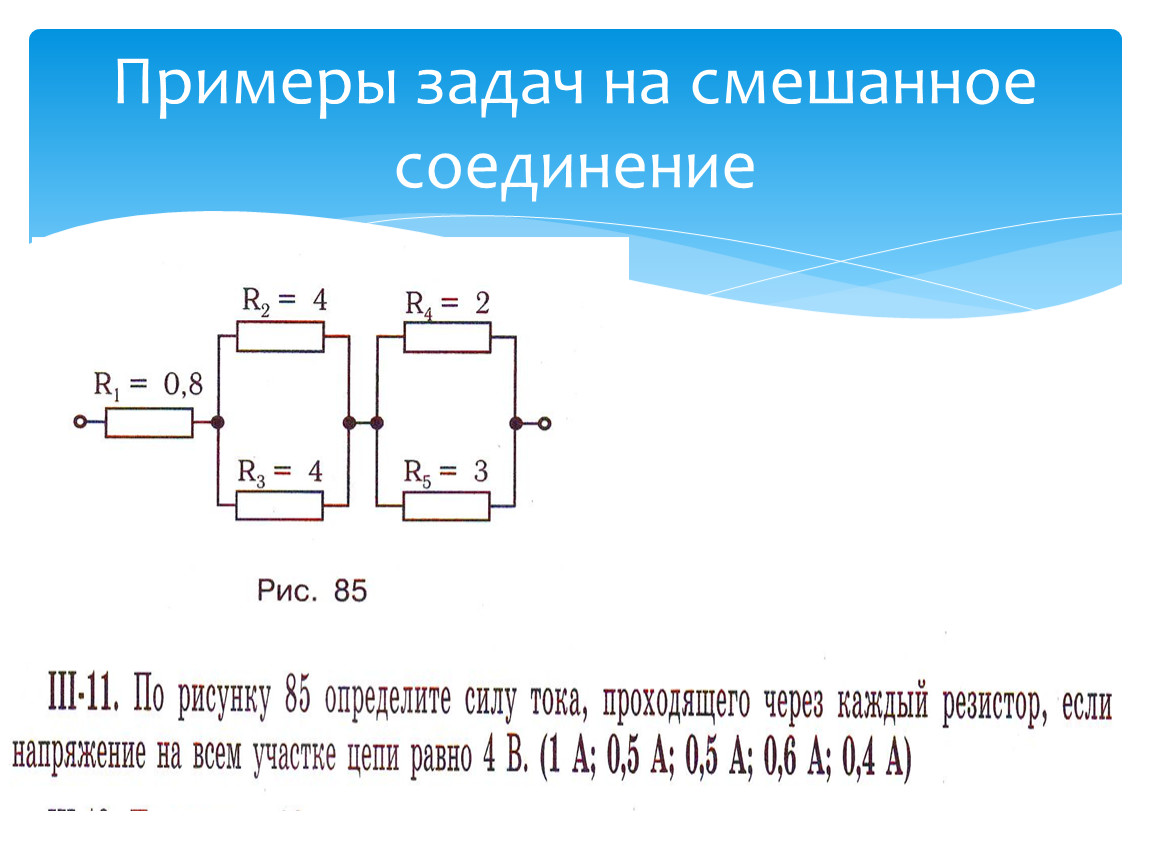
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)
I 2 = 1,125 А
I 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 A
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегии
Два приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Такой подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче могут быть указаны значения резистора, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте условные обозначения, такие как те, что показаны в примере выше.
- При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например I до , I 1 , R 3 , ΔV 2 и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.

- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (на ваш взгляд) параллельную секцию на один резистор, имеющий значение сопротивления, равное эквивалентному сопротивлению параллельной секции.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить .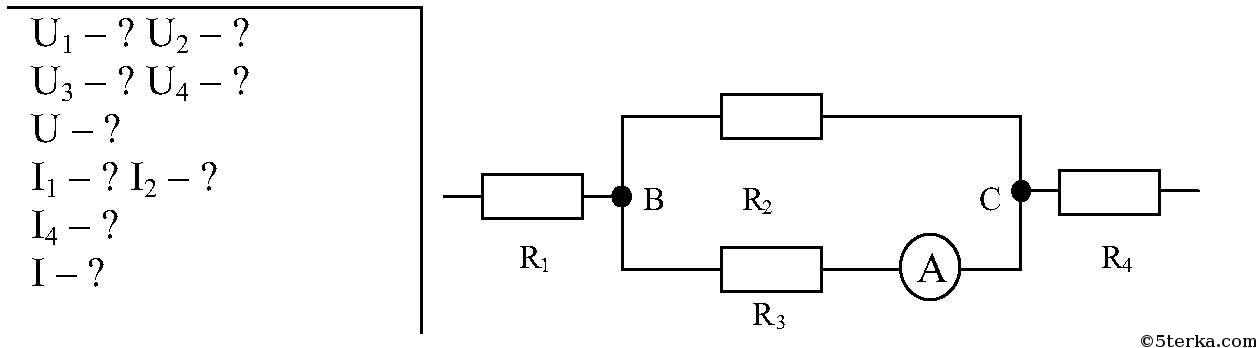 ..
..
Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключать их так, как хотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).
Проверьте свое понимание
1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) току в точке B.
г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.
г. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.
3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.
5. Обращаясь к диаграмме в вопросе №4, определите …
а. … номинальная мощность резистора 4.
г. … скорость, с которой энергия потребляется резистором 3.
Применение последовательного и параллельного соединения проводов.Сопротивление Последовательное и параллельное соединение, Подключение проводов
Содержание:
Во всех электрических цепях используются резисторы — элементы с точно установленным значением сопротивления.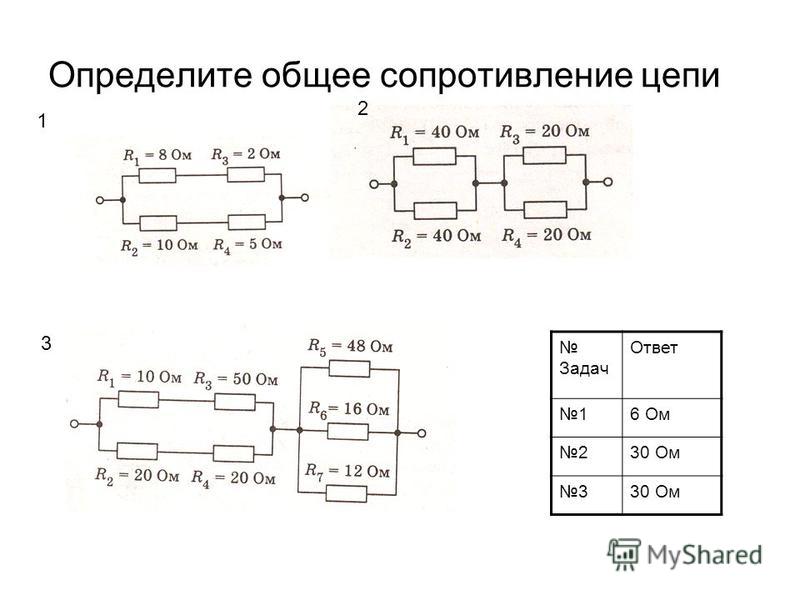 Благодаря специфическим качествам этих устройств появляется возможность регулировать напряжение и силу тока на любых участках цепи. Эти свойства лежат в основе работы практически всех электронных устройств и оборудования. Итак, напряжение при параллельном и последовательном включении резисторов будет отличаться.Поэтому каждый вид компаунда можно использовать только при определенных условиях, чтобы электрическая цепь могла полноценно выполнять свои функции.
Благодаря специфическим качествам этих устройств появляется возможность регулировать напряжение и силу тока на любых участках цепи. Эти свойства лежат в основе работы практически всех электронных устройств и оборудования. Итак, напряжение при параллельном и последовательном включении резисторов будет отличаться.Поэтому каждый вид компаунда можно использовать только при определенных условиях, чтобы электрическая цепь могла полноценно выполнять свои функции.
Последовательное напряжение
При последовательном подключении два резистора больше подключаются к общей цепи таким образом, что каждый из них контактирует с другим устройством только в одной точке. Другими словами, конец первого резистора соединен с началом второго, а конец второго — с началом третьего и т. Д.
Особенностью этой схемы является пропускание через все подключенные резисторы одного и того же электрического тока. По мере увеличения количества элементов в рассматриваемой цепи электрический ток становится все труднее. Это связано с увеличением общего сопротивления резисторов при их последовательном включении. Это свойство отражено в формуле: R общее = R 1 + R 2.
Это связано с увеличением общего сопротивления резисторов при их последовательном включении. Это свойство отражено в формуле: R общее = R 1 + R 2.
Распределение напряжения в соответствии с законом Ома осуществляется на каждом резисторе по формуле: V Rn = i Rn x R n.Таким образом, с увеличением сопротивления резистора падающее на него напряжение увеличивается.
Параллельное напряжение
При параллельном включении включение резисторов в электрическую цепь выполняется таким образом, что все резистивные элементы соединяются между собой сразу обоими контактами. Одна точка, представляющая собой электрический узел, может одновременно подключать несколько резисторов.
Такое соединение предполагает протекание отдельного тока в каждом резисторе.Сила этого тока обратно пропорциональна. В результате происходит увеличение общей проводимости этого участка цепи с общим уменьшением сопротивления. В случае параллельного соединения резисторов с разным сопротивлением значение общего сопротивления в этой области всегда будет ниже наименьшего сопротивления отдельного резистора.
На представленной схеме напряжение между точками A и B — это не только общее напряжение для всей площадки, но и напряжение, приходящее на каждый отдельно взятый резистор.Таким образом, в случае параллельного соединения напряжение, подаваемое на все резисторы, будет одинаковым.
В результате напряжение при параллельном и последовательном подключении будет отличаться в каждом случае. Благодаря этому свойству есть реальная возможность настроить это значение на любом участке цепочки.
Параллельные соединения резисторов, формула для расчета которых выведена из закона Ома и Правил Кирхгофа, являются наиболее распространенным типом включения элементов в электрическую цепь.При параллельном соединении проводов два и более элемента совмещаются своими контактами с обеих сторон соответственно. Соединение их с общей схемой осуществляется этими узловыми точками.
GIF? X15027 «ALT =» (! Lang: общий вид «>!}
Общий вид
Особенности включения
Таким образом, проводники часто включаются в сложные цепи, содержащие, помимо этого, последовательное соединение отдельных секций.
Для такого включения типичны следующие особенности:
- Суммарное напряжение в каждой из ветвей будет иметь одинаковое значение;
- Электрический ток, протекающий в любом из сопротивлений, всегда обратно пропорционален величине их номинала.
В частном случае, когда все включенные параллельно резисторы имеют одинаковые номиналы, то проточные «индивидуальные» токи также будут равны между собой.
Плата
Сопротивление ряда проводящих элементов, соединенных параллельно, определяется известной формой расчета, которая предполагает сложение их проводников (обратное сопротивление величин).
Ток, протекающий в каждом отдельном проводнике в соответствии с законом Ома, можно найти по формуле:
I = u / r (один из резисторов).
После ознакомления с общими принципами работы СКК, элементы сложных цепочек можно обрабатывать на конкретных примерах решения задач этого класса.
Типовые соединения
Пример №1
Часто для решения задачи перед спроектированным конструктором необходимо объединить несколько элементов в результате определенного сопротивления. При рассмотрении простейшего варианта такого решения предполагается, что общее сопротивление цепи из нескольких элементов должно составлять 8 Ом. Этот пример требует отдельного рассмотрения по той простой причине, что в стандартном ряду сопротивлений номинальное значение 8 Ом (их всего 7.5 и 8,2 Ом).
При рассмотрении простейшего варианта такого решения предполагается, что общее сопротивление цепи из нескольких элементов должно составлять 8 Ом. Этот пример требует отдельного рассмотрения по той простой причине, что в стандартном ряду сопротивлений номинальное значение 8 Ом (их всего 7.5 и 8,2 Ом).
Решением этой простейшей задачи можно получить соединение двух одинаковых элементов с сопротивлением до 16 Ом каждый (такие значения в резистивном ряду существуют). По приведенной выше формуле общее сопротивление цепи в этом случае рассчитывается очень просто.
Из него следует:
16х16 / 32 = 8 (ОМ), то есть ровно столько, сколько требуется.
Относительно простым способом можно решить проблему формирования общего сопротивления, равного 8 Ом.
Пример №2.
В качестве еще одного характерного примера формирования необходимого сопротивления можно рассмотреть схему, состоящую из 3-х резисторов.
Общее значение R такого включения можно рассчитать по формуле последовательного и параллельного включения в проводниках.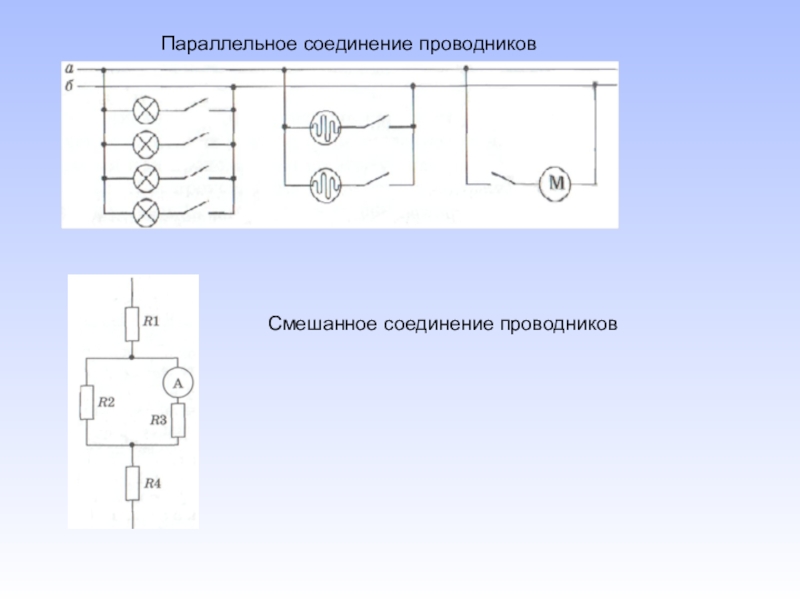
GIF? X15027 «ALT =» (! LANG: Example «>!}
В соответствии со значениями, указанными на картинке, общее сопротивление цепи будет:
1 / R = 1/2 + 1/220 + 1/470 = 0.0117;
R = 1 / 0,0117 = 85,67.
В результате находим суммарное сопротивление всей цепи, полученное путем параллельного соединения трех элементов с номиналами 200, 240 и 470 Ом.
Важно! Указанный метод применим и при подсчете произвольного количества подключенных к параллельным проводам или потребителям.
Также следует отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого маленького номинала.
Расчет комбинированных схем
Рассмотренный метод также может применяться при расчете сопротивлений более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, потому что при формировании цепочек используются сразу оба метода. Смешанный состав резисторов представлен на рисунке ниже.
GIF? X15027 «ALT =» (! Lang: Mixed scheme «>!}
Mixed scheme
Для упрощения расчета сначала разделим все резисторы по типу включения на две независимые группы.Один из них — последовательное подключение, а второй — имеет тип подключения параллельного типа.
Из представленной схемы видно, что элементы R2 и R3 соединены последовательно (объединены в группу 2), которая, в свою очередь, включена параллельно резистору R1, входящему в группу 1.
В предыдущем аннотации было обнаружено, что мощность тока в проводнике зависит от напряжения на его концах. Если в эксперименте изменить проводники, оставив напряжение на них неизменным, можно показать, что при постоянном напряжении на концах проводника ток обратно пропорционален его сопротивлению.Комбинируя зависимость тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = u / r
. Этот закон, установленный экспериментально, называется законом Ома (для участка цепи).
Закон Ома для участка цепи : Сила тока в проводнике прямо пропорциональна напряжению, приложенному к его концам, и обратно пропорциональна сопротивлению проводника. Прежде всего, закон всегда справедлив для твердых и жидких металлических проводников.А также для некоторых других веществ (обычно твердых или жидких).
Потребители электроэнергии (лампочки, резисторы и т. Д.) Могут по-разному подключаться друг к другу в электрической цепи. D. ВА основные типы подключения проводов
: Последовательные и параллельные. И есть еще два редких соединения: смешанное и мостиковое.
Последовательное подключение проводов
При последовательном соединении проводов конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т. Д.Например, подключение электрических лампочек в Рождественской гирлянде. При последовательном соединении проводников ток проходит через все фонари. При этом один и тот же заряд проходит через сечение каждого проводника за единицу времени. То есть заряд не накапливается ни в одной части проводника.
То есть заряд не накапливается ни в одной части проводника.
Следовательно, при последовательном соединении проводов Мощность тока на любом участке цепи одинакова: I 1 =.
I 2 =
I.
.
Общее сопротивление последовательно соединенных проводников равно сумме их сопротивлений : R 1 + R 2 = R
. Потому что при последовательном соединении проводов их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивает сопротивление проводников.
По закону напряжение на каждом проводе составляет: U 1 =.
I *
R 1.
, U 2 = I * R 2
. В этом случае полное напряжение равно U = i (
К 1+.
R 2)
. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно подключенном проводе равно величине напряжений на каждом проводе : U = u 1 + U 2
.
Из тех же уравнений следует, что последовательное соединение проводников используется, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для постоянного подключения проводов действуют справедливые законы
:
1) сила тока во всех проводниках одинакова; 2) напряжение на всем соединении равно величине напряжений на отдельных проводниках; 3) Сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводов
Пример Соединение параллельно Проводники служат для подключения потребителей электрической энергии в квартире. Так вот, параллельно включаются лампочки, чайник, утюг и т. Д.
При параллельном соединении жил все жилы присоединяются к одной точке цепи одним концом. И второй конец к другой точке цепочки. Подключенный к этим точкам вольтметр покажет напряжение и на проводе 1, и на проводе 2.При этом напряжение на концах всех параллельно соединяемых проводников одинаковое: U 1 = U 2 = U
.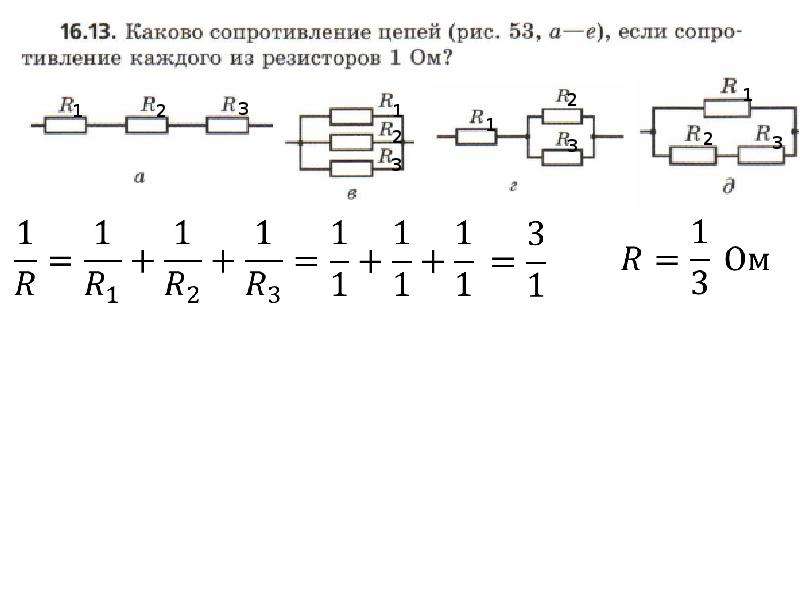
При параллельном соединении жил электрическая цепь разветвляется. Следовательно, часть общего заряда проходит по одному проводнику, а часть — по другому. Следовательно, при параллельном соединении проводников ток в неразрывной части цепи равен величине тока в отдельных проводниках: I =.
I 1+.
I 2.
.
В соответствии с законом Ома I = u / r, i 1 = u 1 / r 1, i 2 = u 2 / r 2
. Отсюда следует: U / r = u 1 / r 1 + u 2 / r 2, u = u 1 = u 2,
1 / R = 1 / R 1 + 1 / R
2
Величина обратного общего сопротивления параллельно подключенным проводам равна сумме обратного сопротивления каждого проводника.
При параллельном соединении жил их общее сопротивление меньше, чем сопротивление каждой жилы. Действительно, если параллельно соединить два проводника с одинаковым сопротивлением g. , то их общее сопротивление составит: R = г / 2 . Это связано с тем, что при параллельном соединении проводников площадь их сечения увеличивается. В результате сопротивление снижается.
Это связано с тем, что при параллельном соединении проводников площадь их сечения увеличивается. В результате сопротивление снижается.
Из полученных формул понятно, почему параллельно включаются потребители электроэнергии.Все они рассчитаны на одно и то же напряжение, которое в квартирах составляет 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. И соответствие общей силы тока предельно допустимой силе.
Для параллельного соединения проводников справедливы законы:
1) напряжение на всех жилах одинаково; 2) мощность тока в месте соединения проводов равна сумме токов в отдельных проводниках; 3) Обратное сопротивление всего соединения равно количеству величин, обратных сопротивлениям отдельных проводников.
Сопротивление проводников. Параллельное и последовательное соединение проводов.
Электрическое сопротивление — Физическая величина, характеризующая свойства проводника по предотвращению прохождения электрического тока и равное отношение на концах проводника к силе тока, протекающего по нему.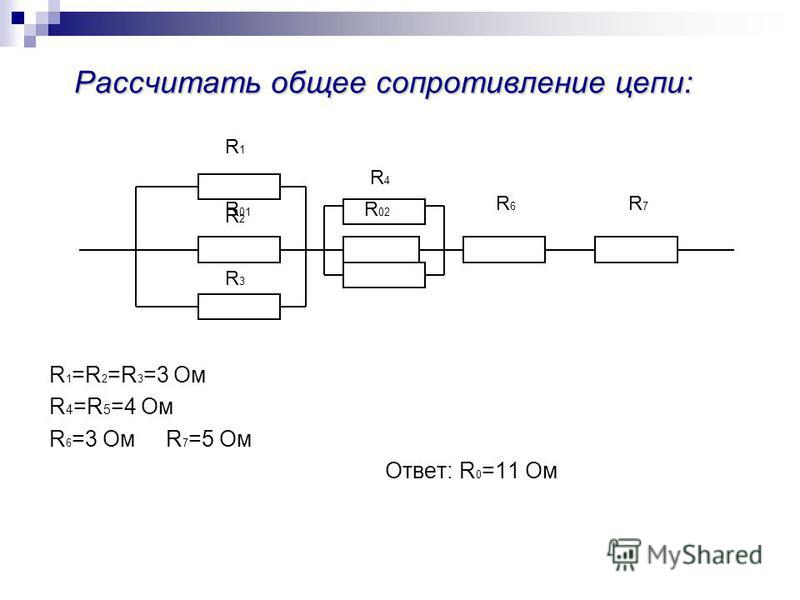 Сопротивление цепей переменного тока и переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления.Сопротивлением (резистором) еще называют радиодетали, предназначенные для введения в электрические цепи активного сопротивления.
Сопротивление цепей переменного тока и переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления.Сопротивлением (резистором) еще называют радиодетали, предназначенные для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R. или R. ) Считается, в определенных пределах, постоянным значением для этого проводника; Его можно рассчитать как
Р. — сопротивление;
U. — разность электрических потенциалов (напряжений) на концах жилы;
I. — Сила тока, протекающего между краями проводника под действием разности потенциалов.
с последовательным подключением
Проводники (рис. 1.9.1) Мощность тока во всех проводниках одинакова:
По закону Ома напряжения U. 1 I. U. 2 на проводниках равны
При последовательном включении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат действителен для любого количества последовательно соединенных проводников.
С параллельным соединением
(рис. 1.9.2) напряжение U. 1 I. U. 2 На обеих направляющих то же:
Этот результат следует из того факта, что в точках разветвления (узлы A. и B. ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A. Во время Δ. т. Комиссия I. Δ t. , и срывается с узла за то же время заряда I. 1 Δ. т. + I. 2 Δ. т. . Следовательно, I. = I. 1 + I. 2.
Запись по закону Ома
При параллельном соединении проводов величина общего сопротивления цепи равна сумме обратных сопротивлений включенного параллельного проводника.
Этот результат справедлив для любого количества включенных параллельных проводников.
Формулы последовательного и параллельного соединения проводов позволяют во многих случаях рассчитать сопротивление сложной цепи, состоящей из множества резисторов.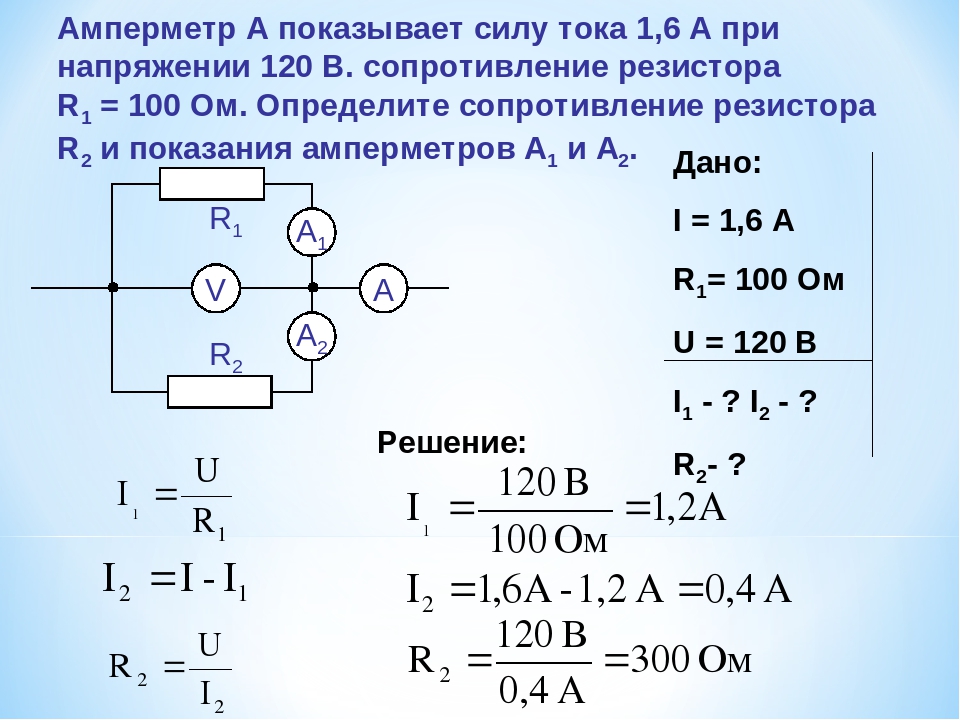 На рис. 1.9.3 Приведен пример такой сложной схемы и указана последовательность расчетов.
На рис. 1.9.3 Приведен пример такой сложной схемы и указана последовательность расчетов.
Следует отметить, что не все сложные цепи, состоящие из проводов с разным сопротивлением, можно рассчитать по формулам для последовательного и параллельного соединения. На рис. 1.9.4 Показан пример электрической схемы, которую невозможно рассчитать указанным выше методом.
При решении задач принято преобразовывать схему, чтобы она была максимально простой.Для этого используются эквивалентные преобразования. Эквивалентными называются такие преобразования части схемы электрической цепи, при которых токи и напряжения в непреобразованной части остаются неизменными.
Существует четыре основных типа подключения проводов: последовательный, параллельный, смешанный и мостовой.
Последовательное соединение
Последовательное соединение — Это соединение, при котором сила тока на всем участке цепи одинакова.Яркий пример последовательного подключения — старинная елочная гирлянда.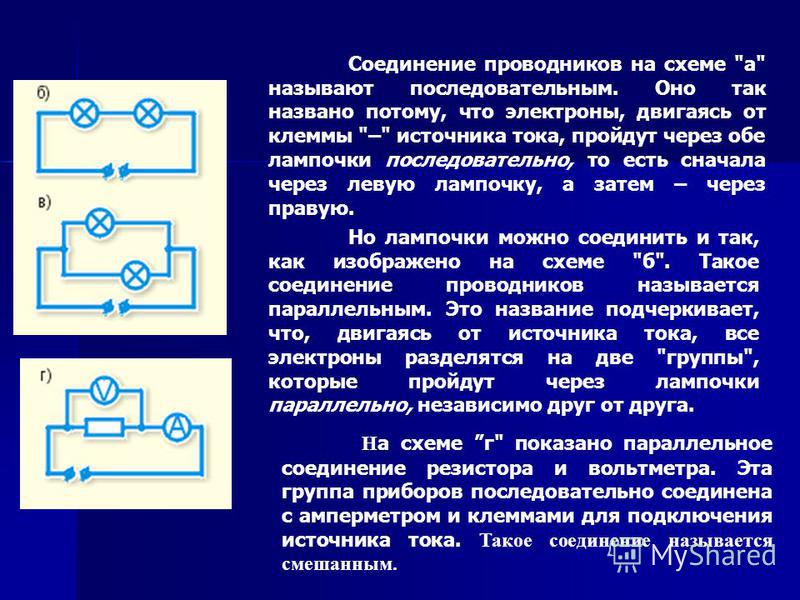 Там лампочки подключены последовательно, друг к другу. А теперь представьте, перегорела одна лампочка, оборвалась цепь, а остальные лампочки ухожены. Отказ одного элемента, приводящий к отказу всех остальных, является существенным недостатком последовательного соединения.
Там лампочки подключены последовательно, друг к другу. А теперь представьте, перегорела одна лампочка, оборвалась цепь, а остальные лампочки ухожены. Отказ одного элемента, приводящий к отказу всех остальных, является существенным недостатком последовательного соединения.
При последовательном включении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение — Это соединение, в котором напряжение на концах участка цепи одинаковое.Параллельное соединение является наиболее распространенным, в основном потому, что все элементы находятся под одним напряжением, ток тока распределяется по-разному, и когда один из элементов выходит, все остальные продолжают работать.
При параллельном подключении эквивалентное сопротивление равно:
В случае двух параллельно включенных резисторов
В случае трех параллельно включенных резисторов:
Смешанное соединение
Смешанное соединение — Соединение, представляющее собой комбинацию последовательных и параллельных соединений. Чтобы найти эквивалентное сопротивление, нужно «минимизировать» схему путем попеременного преобразования параллельных и последовательных участков цепи.
Чтобы найти эквивалентное сопротивление, нужно «минимизировать» схему путем попеременного преобразования параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем добавим к нему оставшееся сопротивление R 3. Следует понимать, что после преобразования эквивалентного сопротивления резистор R 1 R 2 и резистор R 3 соединяются последовательно.
Итак, остались самые интересные и сложные соединения проводников.
Мостовая схема
Мостовая схема подключения показана на рисунке ниже.
Чтобы минимизировать мост, один из треугольников моста заменяется эквивалентной звездой.
И найдите сопротивление R 1, R 2 и R 3.
Последовательное и параллельное соединение проводов резистора. Параллельное соединение сопротивлений (резисторов)
1. При последовательном подключении проводов
1. Сила тока во всех проводниках одинакова :
Сила тока во всех проводниках одинакова :
I 1 = I 2 = I
2.
Общее напряжение U на обоих проводниках равно сумме напряжений U 1 и U 2 на каждом проводе :
U
= U 1 + U 2
3. закон Ома, напряжения U 1 и U 2 на проводниках равны U 1 = IR 1, U 2 = IR 2 общее напряжение U = IR Где R — это электрическое сопротивление всей цепи, тогда
IR = IR 1 + I R 2. Отсюда следует
R =
R 1
+
R 2
Импеданс последовательной цепи равен сумме сопротивлений отдельных проводов.
Этот результат действителен для любого количества последовательно соединенных проводов.
2.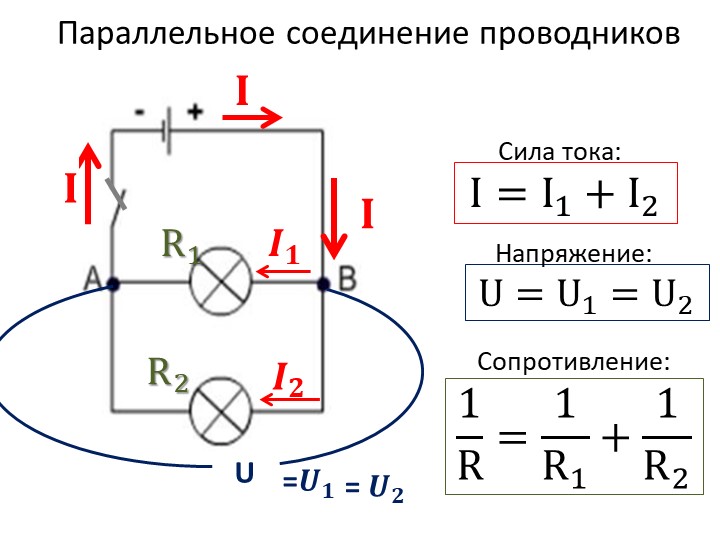 При параллельном подключении проводов
При параллельном подключении проводов
1.
Напряжение U 1 и U 2 на обоих проводниках одинаковы
U
1 = U 2 = U
2.
Сумма токов I 1 + I 2, , протекающая по обоим проводникам, равна току в неразветвленной цепи :
I = I 1 + I 2
Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи заряды постоянного тока не могут накапливаться.Например, к узлу A во времени Δ t утечки заряда I Δ t , и заряд одновременно уходит от узла I 1 Δ t + I 2 Δ t … Следовательно, I = I 1 + I 2.
3.
Письмо, основанное на законе Ома
, где R — электрическое сопротивление всей цепи, получаем
При параллельном соединении проводов величина, обратная общему сопротивлению цепи, равна сумме значений, обратных сопротивлениям параллельно соединенных проводников.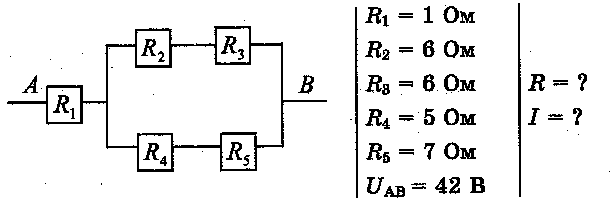
Этот результат действителен для любого количества параллельно соединенных проводов.
Формулы последовательного и параллельного соединения проводов позволяют во многих случаях рассчитать сопротивление сложной цепи, состоящей из множества резисторов. На рисунке показан пример такой сложной схемы и показана последовательность расчетов. Сопротивления всех проводов указаны в омах (Ом).
На практике одного источника тока в цепи недостаточно, и тогда источники тока также соединяются между собой для питания цепи.Подключение источников к батарее может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединены противоположными полюсами.
То есть, чтобы соединить батареи последовательно, положительный полюс первой батареи подключается к «плюсу» электрической цепи. Положительный полюс второй батареи подключается к ее отрицательной клемме и т. Д. Отрицательная клемма последней батареи подключается к «минусу» электрической цепи.
Полученная последовательно включенная батарея имеет ту же емкость, что и одиночная батарея, а напряжение такой батареи равно сумме напряжений включенных в нее батарей. Те. если батареи имеют одинаковое напряжение, то напряжение батареи равно напряжению одной батареи, умноженному на количество батарей в батарее.
1.
ЭДС аккумулятора равна сумме ЭДС отдельных источников ε = ε 1 + ε 2 + ε 3
2
.
Суммарное сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батарея = r 1 + r 2 + r 3
Если к аккумулятору подключено n одинаковых источников, то ЭДС аккумулятора ε = nε 1, а сопротивление r аккумулятора = nr 1
3.
При параллельном подключении подключите все положительные и все отрицательные полюса двух источников n.
То есть при параллельном подключении батареи соединяются так, что положительные выводы всех батарей соединяются с одной точкой электрической цепи («плюс»), а отрицательные выводы всех батарей соединяются с другой точкой электрической цепи. цепь («минус»).
цепь («минус»).
Подключайте только параллельно источников от такую же ЭДС … Получающаяся при параллельном подключении батарея имеет такое же напряжение, как и у одиночной батареи, а емкость такой батареи равна сумме емкостей батареи, входящие в него.Те. если батареи имеют одинаковую емкость, то емкость батареи равна емкости одной батареи, умноженной на количество батарей в батарее.
1.
ЭДС батареи идентичных источников равна ЭДС одного источника. ε = ε 1 = ε 2 = ε 3
2.
Сопротивление батареи меньше сопротивления одного источника r батарея = r 1 / n
3.
Сила тока в такой цепи по закону Ома
Электрическая энергия, запасенная в аккумуляторной батарее, равна сумме энергий отдельных батарей (произведение энергий отдельных батарей, если батареи одинаковые), независимо от того, подключены ли батареи параллельно или последовательно. .
Внутреннее сопротивление аккумуляторов, изготовленных по той же технологии, примерно обратно пропорционально емкости аккумулятора. Следовательно, поскольку при параллельном подключении емкость аккумулятора равна сумме емкостей включенных в него аккумуляторов, то есть увеличивается, то внутреннее сопротивление уменьшается.
Следовательно, поскольку при параллельном подключении емкость аккумулятора равна сумме емкостей включенных в него аккумуляторов, то есть увеличивается, то внутреннее сопротивление уменьшается.
Параллельное соединение сопротивлений — это такое соединение, когда начало сопротивлений подключено к одной общей точке, а концы — к другой.
Параллельное соединение сопротивлений имеет следующие свойства:
Напряжения на выводах всех сопротивлений одинаковы:
U 1 = U 2 = U 3 = U;
Проводимость всех параллельно соединенных сопротивлений равна сумме проводимости отдельных сопротивлений:
1 / R = 1 / R 1 + 1 / R 2 + 1 / R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 / R 1 R 2 R 3,
где R — эквивалентное (результирующее) сопротивление трех сопротивлений (в данном случае R 1, R 2 и R 3).
Для получения сопротивления такой цепи необходимо перевернуть дробь, определяющую значение ее проводимости. Следовательно, сопротивление параллельного разветвления трех резисторов:
R = R 1 R 2 R 3 / R 1 R 2 + R 2 R 3 + R 1 R 3.
Эквивалентное сопротивление — это сопротивление, которое может заменить несколько сопротивлений (подключенных параллельно или последовательно) без изменения величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимость всех отдельных секций, т.е.е. найти полную проводимость. Суммарная проводимость — это полное сопротивление, обратное величине.
При параллельном подключении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, поэтому эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно подключенных сопротивлений.
На практике могут быть случаи, когда цепочка состоит из более чем трех параллельных ветвей. Все полученные соотношения остаются в силе для схем, состоящих из любого количества параллельно включенных резисторов.
Найдем эквивалентное сопротивление двух параллельно соединенных сопротивлений R 1 и R 2 (см. Рис.). Электропроводность первой ветви составляет 1 / R 1, проводимость второй ветви составляет 1 / R 2 .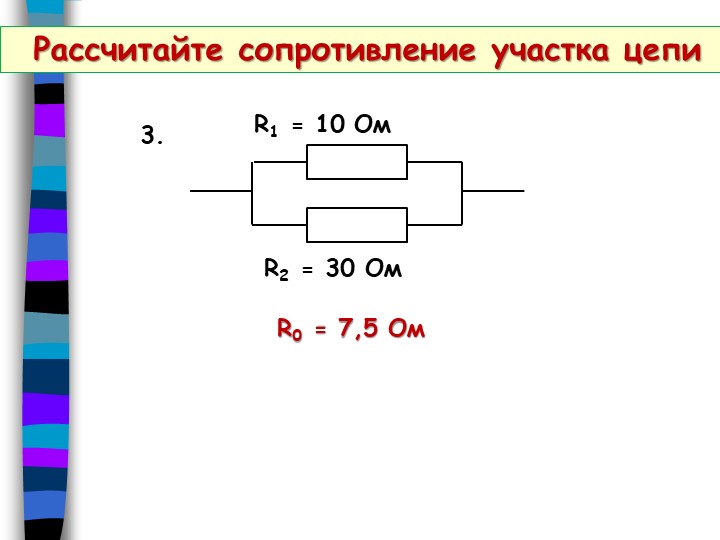 .. Общая проводимость:
.. Общая проводимость:
1 / R = 1 / R 1 + 1 / R 2.
Подведем к общему знаменателю:
1 / R = R 2 + R 1 / R 1 R 2,
, следовательно, эквивалентное сопротивление
R = R 1 R 2 / R 1 + R 2.
Эта формула используется для расчета общего сопротивления цепи, состоящей из двух параллельно соединенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно соединенных сопротивлений равно произведению этих сопротивлений на их сумму.
Параллельное соединение с одинаковым сопротивлением R 1 их эквивалентное сопротивление будет в несколько раз меньше, т. Е.
R = R 1 / n.
В диаграмме, показанной на последнем рисунке, включены пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R составит
R = R 1/5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, приближающихся к узловой точке A (на первом рисунке), равна сумме выходящих из нее токов:
Я = Я 1 + Я 2 + Я 3.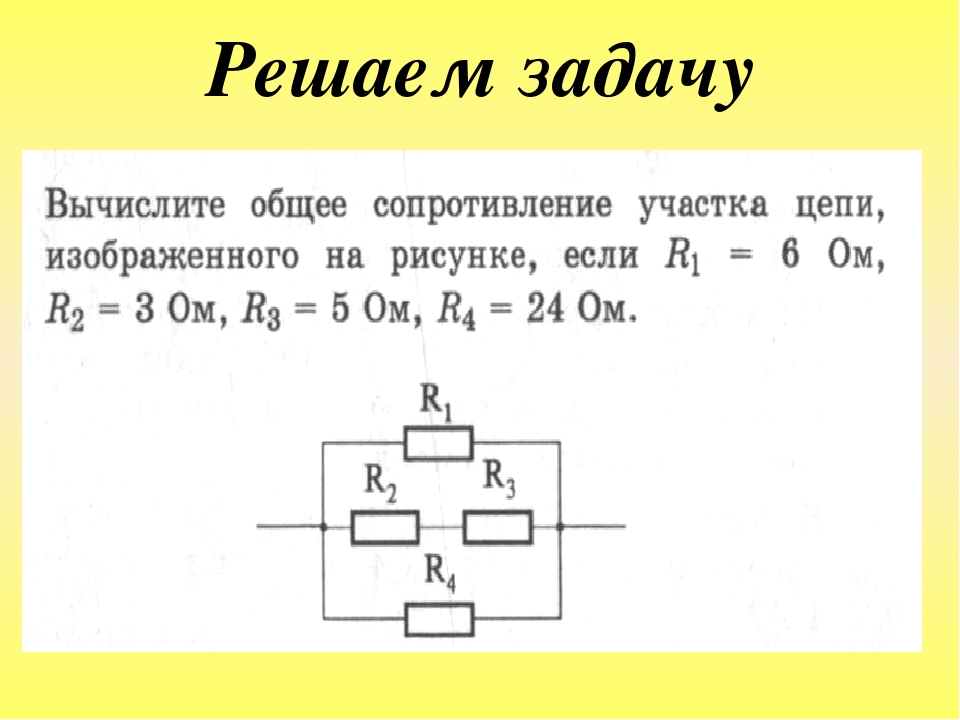
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Поскольку напряжение на выводах этих сопротивлений одинаковое, то
U = I 1 R 1 и U = I 2 R 2.
Левые части этих равенств совпадают, следовательно, правые части также равны:
I 1 R 1 = I 2 R 2,
или
I 1 / I 2 = R 2 / R 1,
Тех. ток при параллельном соединении ветвей сопротивлений обратно пропорционален сопротивлениям ветвей (или прямо пропорционален их проводимости).Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с большей рассеиваемой мощностью.
При параллельном подключении неравных резисторов резистор с наивысшим сопротивлением дает наибольшую мощность.
Пример 1. Два резистора включены параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить полное сопротивление цепи R total
Решение. R total = R 1 R 2 / R 1 + R 2 = 25. 50/25 + 50 ≈ 16,6 Ом.
R total = R 1 R 2 / R 1 + R 2 = 25. 50/25 + 50 ≈ 16,6 Ом.
Пример 2. В ламповом усилителе три лампы, нити накаливания которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1,5 ампера и третьей I 3 = 2,5 ампера. Определить полный ток цепей накаливания лампы усилителя I total.
Решение. I total = I 1 + I 2 + I 3 = 1 + 1,5 + 2,5 = 5 ампер.
Резисторы параллельного подключения часто встречаются в радиооборудовании.Два или более резистора подключаются параллельно в случаях, когда ток в цепи слишком велик и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения электрической энергии потребителей может служить включение электрических ламп обычной осветительной сети, которые включаются параллельно. Преимущество параллельного подключения потребителей в том, что отключение одного из них не влияет на работу других.
Последовательное, параллельное и смешанное включение резисторов.
Значительное количество включенных в электрическую цепь приемников (электрические лампы, электронагревательные приборы и т. Д.) Можно рассматривать как элементы, имеющие определенное сопротивление . Данное обстоятельство дает нам возможность при составлении и изучении электрических схем заменить конкретные приемники резисторами с определенными сопротивлениями. Существуют следующие способы подключения резисторов (приемников электрической энергии): последовательный, параллельный и смешанный.
Д.) Можно рассматривать как элементы, имеющие определенное сопротивление . Данное обстоятельство дает нам возможность при составлении и изучении электрических схем заменить конкретные приемники резисторами с определенными сопротивлениями. Существуют следующие способы подключения резисторов (приемников электрической энергии): последовательный, параллельный и смешанный.
Последовательное соединение резисторов .
Последовательное соединение нескольких резисторов, конец первого резистора подключается к началу второго, конец второго — к началу третьего и т. Д. При таком подключении все элементы последовательной цепи проходят
одинаково ток I.
Последовательное подключение приемников показано на рис. 25, а.
Заменив лампы на резисторы с сопротивлениями R1, R2 и R3, получаем схему, показанную на рис.25, корп.
Если предположить, что в источнике Ro = 0, то для трех последовательно включенных резисторов по второму закону Кирхгофа можно записать:
E = IR 1 + IR 2 + IR 3 = I (R 1 + R 2 + R 3) = IR экв (19)
где R eq = R 1 + R 2 + R 3.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Поскольку напряжения на отдельных участках цепи по закону Ома: U 1 = IR 1; U 2 = IR 2, U 3 = IR s и в данном случае E = U, то для рассматриваемой схемы
U = U 1 + U 2 + U 3
(20)
Следовательно, напряжение U на клеммах истока равно сумме напряжений на каждом из последовательно соединенных резисторов.
Из этих формул также следует, что напряжения распределяются между последовательно включенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
, то есть чем больше сопротивление любого приемника в последовательной цепи, тем больше приложенное к нему напряжение.
Если несколько, например n, резисторов с одинаковым сопротивлением R1 соединены последовательно, эквивалентное сопротивление цепи Rek будет в n раз больше сопротивления R1, i.е. Рек = nR1. Напряжение U1 на каждом резисторе в этом случае в n раз меньше полного напряжения U:
Напряжение U1 на каждом резисторе в этом случае в n раз меньше полного напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них немедленно влечет за собой изменение напряжения на других подключенных к нему приемниках. При отключении или прерывании электрической цепи в одном из приемников и в остальных приемниках ток прекращается. Поэтому последовательное подключение приемников применяется редко — только в том случае, если напряжение источника электроэнергии больше номинального напряжения, на которое рассчитан потребитель.Например, напряжение в электрической сети, от которой питаются вагоны метро, составляет 825 В, а номинальное напряжение электрических ламп, используемых в этих вагонах, составляет 55 В. Таким образом, в вагонах метро электрические лампы включают 15 ламп последовательно в каждый контур.
Параллельное соединение резисторов . Параллельное соединение нескольких приемников, они соединяются между двумя точками электрической цепи, образуя параллельные ответвления (рис. 26, а). Замена
26, а). Замена
ламп с резисторами с сопротивлениями R1, R2, R3, получаем схему, показанную на рис.26, корп.
При параллельном включении на все резисторы подается одинаковое напряжение U. Следовательно, по закону Ома:
I 1 = U / R 1; I 2 = U / R 2; I 3 = U / R 3.
Ток в неразветвленной части цепи по первому закону Кирхгофа I = I 1 + I 2 + I 3, или
I = U / R 1 + U / R 2 + U / R 3 = U (1 / R 1 + 1 / R 2 + 1 / R 3) = U / R экв (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном включении трех резисторов определяется по формуле
1/ R экв
=
1 / правая 1 + 1 / правая 2 + 1 / правая 3 (24)
Путем введения в формулу (24) вместо значений 1 / R eq, 1 / R 1, 1 / R 2 и 1 / R 3, соответствующих проводимости G eq, G 1, G 2 и G 3 , получаем: эквивалент проводимости параллельной цепи, равной сумме сопротивлений параллельно включенных резисторов :
G экв = G 1 + G 2 + G 3
(25)
Таким образом, с увеличением количества параллельно включенных резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных выше формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическому сопротивлению или прямо пропорционально их проводимости. Например, с тремя ветками
I 1: I 2: I 3 = 1 / R 1: 1 / R 2: 1 / R 3 = G 1 + G 2 + G 3 (26)
В этом отношении существует полная аналогия между распределением токов в отдельных ответвлениях и распределением потоков воды по трубам.
Приведенные выше формулы позволяют определить сопротивление эквивалентной цепи для различных конкретных случаев … Например, при параллельном включении двух резисторов результирующее сопротивление цепи составляет
R eq = R 1 R 2 / (R 1 + R 2)
с тремя параллельно включенными резисторами
R экв = R 1 R 2 R 3 / (R 1 R 2 + R 2 R 3 + R 1 R 3)
Когда несколько, например n, резисторов с одинаковым сопротивлением R1 соединены параллельно, результирующее сопротивление цепи Rek будет в n раз меньше сопротивления R1, i. е.
е.
R eq = R1 / n (27)
Ток I1, проходящий через каждую ветвь, в этом случае будет в n раз меньше полного тока:
I1 = I / n (28)
При параллельном подключении приемников все они находятся под одинаковым напряжением, и режим работы каждого из них не зависит от других. Это означает, что ток, проходящий через какой-либо из приемников, не окажет существенного влияния на другие приемники.При любом отключении или отказе любого приемника остальные приемники остаются включенными.
ченны. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, в результате чего оно стало наиболее распространенным. В частности, электрические лампы и двигатели, рассчитанные на работу при определенном (номинальном) напряжении, всегда подключаются параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели должны включаться при разных напряжениях во время регулирования скорости, поэтому они переключаются с последовательного на параллельный режим во время разгона.
Смешанное подключение резисторов . Смешанное соединение называется соединением, при котором некоторые резисторы включены последовательно, а некоторые — параллельно. Например, на схеме рис.27, а есть два последовательно включенных резистора с сопротивлениями R1 и R2, резистор с сопротивлением R3 подключен параллельно им, а резистор с сопротивлением R4 — последовательно с группой резисторов с сопротивлениями R1, R2 и R3.
Сопротивление эквивалентной цепи в смешанном соединении обычно определяется методом преобразования, при котором сложная цепь последовательно преобразуется в простую.Например, для схемы на рис. 27, а сначала определите эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. В этом случае схема на рис. 27, а заменяется схемой замещения на рис. 27, б. Тогда эквивалентное сопротивление R123 параллельно соединенных сопротивлений и R3 определяется по формуле
R 123 = R 12 R 3 / (R 12 + R 3) = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3).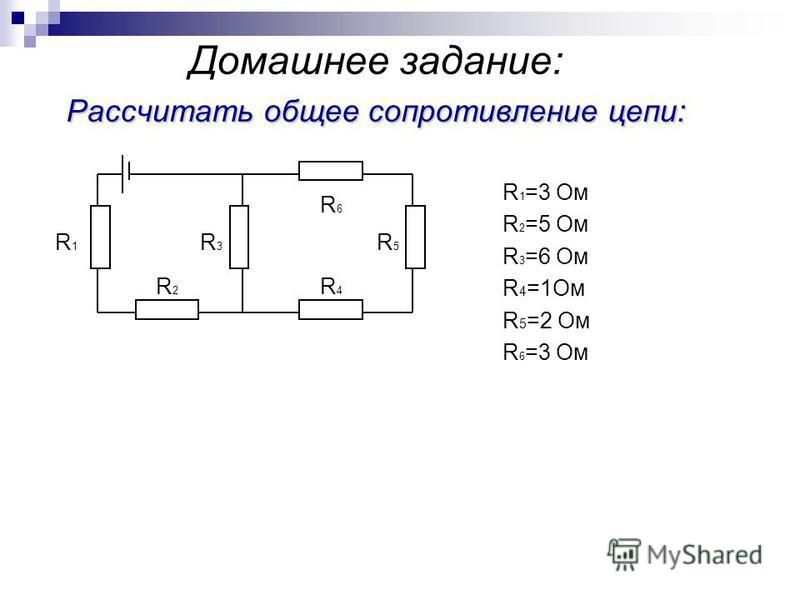
В этом случае диаграмма на рис.27, б заменена эквивалентной схемой на рис. 27, в. После этого эквивалентное сопротивление всей цепи находится путем суммирования сопротивления R123 и сопротивления R4, включенных последовательно с ним:
R eq = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательные, параллельные и смешанные соединения широко используются для изменения сопротивления пусковых реостатов при пуске e. п. от. постоянный ток.
Как отличить параллельное соединение от последовательного.Параллельное и последовательное соединение проводов
Ток в цепи течет по проводникам к нагрузке от источника. В качестве таких элементов чаще всего используется медь. Схема может иметь несколько электрических приемников. Их сопротивления различаются. В электрической цепи проводники могут быть соединены параллельно или последовательно. Бывают и смешанные его виды. Разницу между каждым из них следует знать перед выбором строения электрической схемы.
Проводники и элементы схемы
Ток течет по проводникам. Следует от источника к загрузке. В этом случае проводник должен легко выделять электроны.
Провод с сопротивлением называется резистором. Напряжение этого элемента представляет собой разность потенциалов между концами резистора, которая соответствует направлению потока мощности.
Последовательное и параллельное соединение проводов характеризуется одним общим принципом.Ток течет в цепи от плюса (он называется источником) к минусу, где потенциал становится все меньше и меньше, уменьшается. В электрических схемах сопротивление проводов считается нулевым, так как им можно пренебречь.
Поэтому при расчете последовательного или параллельного подключения прибегают к идеализации. Это облегчает их изучение. В реальных схемах потенциал постепенно уменьшается при движении по проводу и элементам, имеющим параллельное или последовательное соединение.
Последовательное соединение проводов
При последовательном соединении проводов сопротивления включаются одно за другим.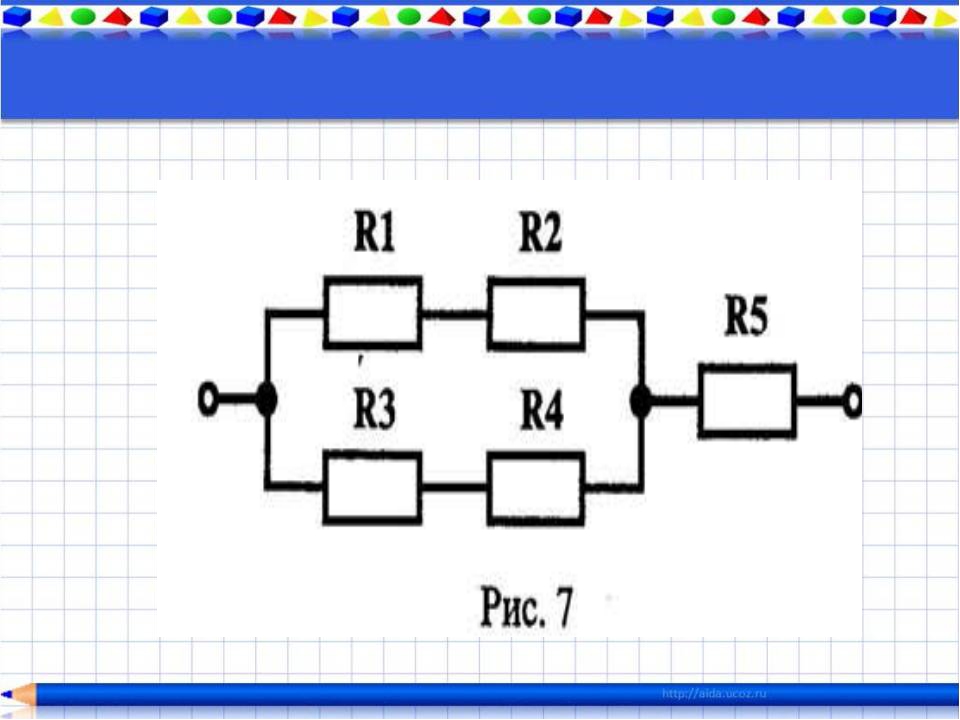 В этом положении сила тока во всех элементах схемы одинакова. Последовательно соединенные проводники создают в сечении напряжение, равное их сумме на всех элементах.
В этом положении сила тока во всех элементах схемы одинакова. Последовательно соединенные проводники создают в сечении напряжение, равное их сумме на всех элементах.
Заряды не имеют возможности накапливаться в узлах цепочки. Это привело бы к изменению напряжения электрического поля и силы тока.
При наличии постоянного напряжения ток будет зависеть от сопротивления цепи. Поэтому при последовательном подключении сопротивление изменится из-за изменения одной нагрузки.
Последовательное соединение проводов имеет недостаток. При выходе из строя одного из элементов схемы работа всех остальных ее компонентов будет прервана. Например, как в гирлянде. Если в нем перегорит одна лампочка, все изделие не пойдет.
Если проводники были соединены последовательно в цепи, их сопротивление в каждой точке будет одинаковым.Сопротивление в сумме всех элементов схемы будет равно сумме падений напряжения на участках схемы.
Это подтверждается опытом. Последовательное соединение сопротивлений рассчитывается с помощью инструментов и математической проверки. Например, возьмем три постоянных сопротивления известной величины. Их подключают последовательно и подключают к источнику питания 60 В.
Например, возьмем три постоянных сопротивления известной величины. Их подключают последовательно и подключают к источнику питания 60 В.
После этого рассчитываются оценочные показатели устройств, если цепь замкнута.По закону Ома находится ток в цепи, который определит падение напряжения на всех ее участках. После этого полученные результаты суммируются и получается суммарное значение уменьшения сопротивления во внешней цепи. Последовательное соединение сопротивлений можно подтвердить приблизительно. Если не учитывать внутреннее сопротивление, создаваемое источником энергии, то падение напряжения будет меньше суммы сопротивлений. По приборам видно, что равенство примерно соблюдается.
Параллельное соединение проводов
При последовательном и параллельном соединении проводов в цепи используются резисторы. Параллельное соединение проводников — это система, в которой одни концы всех резисторов сходятся к одному общему узлу, а другие концы — к другому узлу. В этих местах сходятся более двух проводников.
При таком подключении на элементы подается такое же напряжение. Параллельные участки цепи называются ветвями. Они проходят между двумя узлами.Параллельное и последовательное соединение имеют свои свойства.
Если в электрической цепи есть ответвления, то напряжение на каждой из них будет одинаковым. Оно равно напряжению на неразветвленном участке. На этом этапе сила тока будет рассчитана как сумма его в каждой ветви.
Значение, равное сумме индикаторов, обратных сопротивлениям ответвлений, также будет обратным сопротивлению участка параллельного соединения.
Параллельное соединение резисторов
Параллельное и последовательное соединение различаются расчетом сопротивлений его элементов.При параллельном подключении ток разветвляется. Это увеличивает проводимость цепи (уменьшает общее сопротивление), которое будет равно сумме проводимости ветвей.
Если несколько резисторов одного номинала соединены параллельно, то общее сопротивление цепи будет меньше, чем на один резистор, столько раз, сколько они включены в цепь.
Последовательное и параллельное соединение проводов имеет ряд особенностей. При параллельном подключении ток обратно пропорционален сопротивлению.Токи в резисторах не зависят друг от друга. Поэтому отключение одного из них не повлияет на работу остальных. Поэтому многие электроприборы имеют именно такой тип соединения элементов схемы.
Смешанный
Параллельное и последовательное соединение проводов можно объединить в одну цепь. Например, элементы, соединенные параллельно друг другу, могут быть соединены последовательно с другим резистором или их группой. Это смешанное соединение.Общее сопротивление цепей рассчитывается путем отдельного сложения значений для параллельно включенного блока и для последовательного соединения.
Причем сначала рассчитываются эквивалентные сопротивления элементов, соединенных последовательно, а затем рассчитывается общее сопротивление параллельных участков цепи. Последовательное соединение имеет приоритет в расчетах. Подобные схемы подключения довольно часто встречаются в различных устройствах и оборудовании.
Подобные схемы подключения довольно часто встречаются в различных устройствах и оборудовании.
Ознакомившись с видами соединения элементов схемы, можно понять принцип организации схем различных электрических устройств.Параллельное и последовательное соединение имеют ряд особенностей расчета и функционирования всей системы. Зная их, можно правильно применить каждый из представленных видов для соединения элементов электрических схем.
В уроке рассматривается параллельное соединение проводов. Изображена схема такого подключения, показано выражение для расчета силы тока в такой цепи. Также вводится понятие эквивалентного сопротивления, найдено его значение для случая параллельного включения.
Подключение проводов другое. Они могут быть параллельными, последовательными и смешанными. В этом уроке мы рассмотрим параллельное соединение проводников и понятие эквивалентного сопротивления.
Параллельное соединение проводов — это соединение, при котором начало и конец проводов соединены вместе.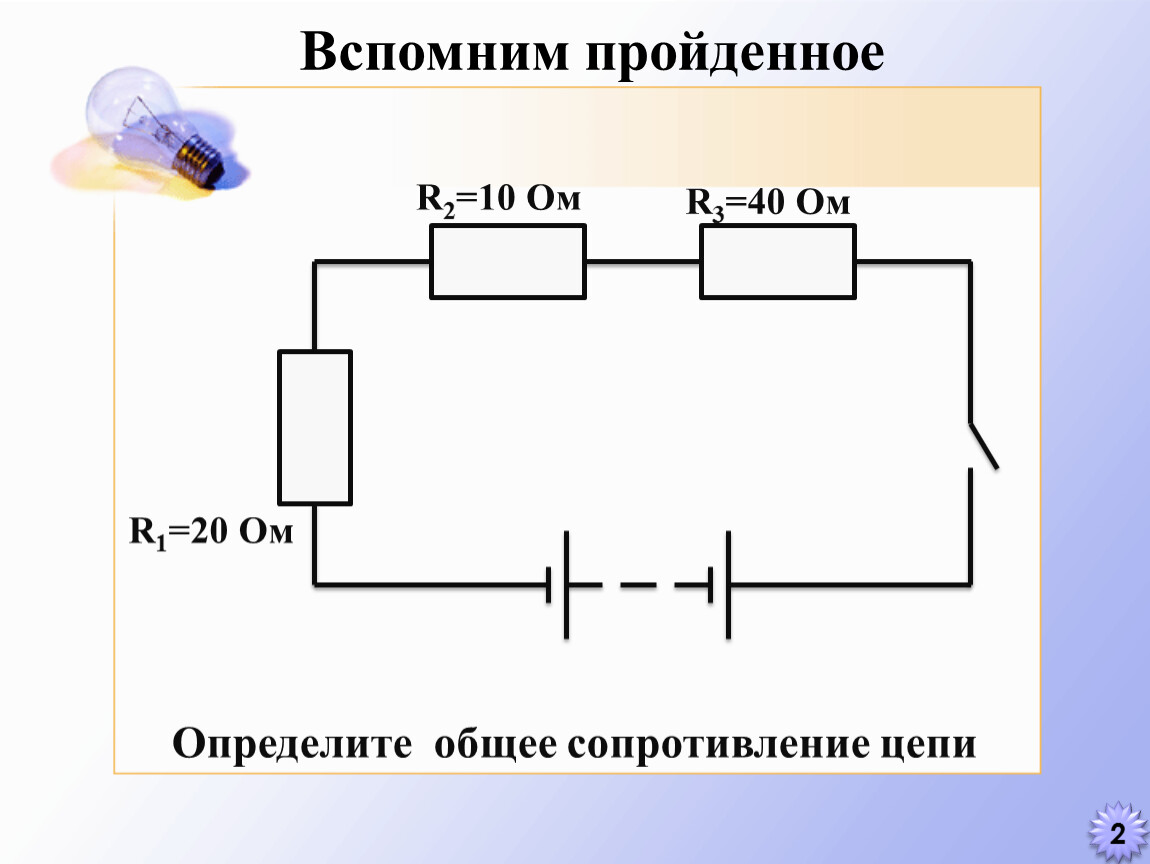 На схеме такое подключение обозначено следующим образом (рис.1):
На схеме такое подключение обозначено следующим образом (рис.1):
Рис. 1. Параллельное соединение трех резисторов
На рисунке показаны три резистора (устройство, основанное на сопротивлении проводника) с сопротивлениями R1, R2, R3.Как видите, начала этих проводников соединены в точке A, концы — в точке B, и они расположены параллельно друг другу. Также в цепи может быть больше параллельно соединенных проводов.
Теперь рассмотрим следующую схему (рис. 2):
Рис. 2. Схема исследования силы тока при параллельном соединении проводов
В качестве элементов схемы взяли две лампы (1а, 1б). У них тоже есть свое сопротивление, поэтому мы можем считать их наравне с резисторами.Эти две лампы соединены параллельно, они подключены в точках A и B. У каждой лампы свой амперметр: A1 и A2 соответственно. Также есть амперметр A 3, который измеряет ток во всей цепи. В схему также входят блок питания (3) и ключ (4).
Закрыв ключ, будем следить за показаниями амперметров. Амперметр A 1 покажет силу тока равную I 1 в лампе 1a, амперметр A 2 — силу тока равную I 2 в лампе 1b. Что касается амперметра А 3, то он покажет силу тока, равную сумме токов в каждой взятой отдельно взятой цепи, включенной параллельно: I = I 1 + I 2.То есть, если сложить показания амперметров А1 и А2, мы получим показания амперметра А3.
Амперметр A 1 покажет силу тока равную I 1 в лампе 1a, амперметр A 2 — силу тока равную I 2 в лампе 1b. Что касается амперметра А 3, то он покажет силу тока, равную сумме токов в каждой взятой отдельно взятой цепи, включенной параллельно: I = I 1 + I 2.То есть, если сложить показания амперметров А1 и А2, мы получим показания амперметра А3.
Стоит отметить, что если одна из ламп перегорит, то вторая продолжит работу. В этом случае весь ток будет проходить через вторую лампу. Это очень удобно. Так, например, электрические приборы в наших домах соединены параллельно в цепь. А при выходе из строя одного из них остальные остаются в рабочем состоянии.
Рис. 3. Схема определения эквивалентного сопротивления при параллельном включении
На схеме рис.3 мы оставили один амперметр (2), но добавили в электрическую цепь вольтметр (5) для измерения напряжения. Точки A и B являются общими как для первой (1a), так и для второй лампы (1b), что означает, что вольтметр измеряет напряжение на каждой из этих ламп (U 1 и U 2) и во всей цепи (U). Тогда U = U 1 = U 2.
Тогда U = U 1 = U 2.
Эквивалентное сопротивление — это сопротивление, которое может заменить все элементы, включенные в данную цепь. Посмотрим, чему он будет равен при параллельном подключении.Из закона Ома вы можете получить это:
В этой формуле R — эквивалентное сопротивление, R 1 и R 2 — сопротивление каждой лампочки, U = U 1 = U 2 — напряжение, которое показывает вольтметр (5). При этом используем тот факт, что сумма токов в каждой отдельной цепи равна полному току (I = I 1 + I 2). Отсюда вы можете получить формулу эквивалентного сопротивления:
Если в цепи больше элементов, включенных параллельно, то и термов будет больше.Затем нужно вспомнить, как работать с простыми дробями.
Следует отметить, что при параллельном подключении эквивалентное сопротивление будет довольно небольшим. Соответственно, сила тока будет достаточно большой. Это следует учитывать при подключении большого количества электроприборов. Ведь тогда сила тока увеличится, что может привести к перегреву проводов и возгоранию.
В следующем уроке мы рассмотрим другой тип проводного подключения — последовательное.
Список литературы
- Генденштейн Л.Е., Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзен И.И. — М .: Мнемозина.
- А.В. Перышкин Физика 8. — М .: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. — М .: Просвещение.
.
- Физика ().
- Суперзадача ().
- Интернет-портал Nado5.ru ().
Домашнее задание
- П.114-117: вопросы № 1-6. СРЕДНИЙ. Перышкин Физика 8. — М .: Дрофа, 2010.
- Можно ли параллельно подключить более трех проводов?
- Что произойдет, если перегорит одна из двух параллельно соединенных ламп?
- Если к какой-либо цепи параллельно подключить еще один провод, всегда ли будет уменьшаться его эквивалентное сопротивление?
.
При решении задач принято преобразовывать схему, чтобы она была максимально простой. Для этого используются эквивалентные преобразования.Такие преобразования части электрической цепи называются эквивалентными, при которых токи и напряжения в ее непреобразованной части остаются неизменными.
Для этого используются эквивалентные преобразования.Такие преобразования части электрической цепи называются эквивалентными, при которых токи и напряжения в ее непреобразованной части остаются неизменными.
Существует четыре основных типа подключения проводов: последовательный, параллельный, смешанный и мостовой.
Последовательное соединение
Последовательное соединение — это такое соединение, при котором сила тока одинакова по всей цепи. Яркий пример последовательного подключения — старая елочная гирлянда.Там лампочки включаются последовательно, одна за другой. А теперь представьте, перегорела одна лампочка, оборвалась электрическая цепь, а остальные лампочки погасли. Выход из строя одного элемента приводит к отключению всех остальных, это существенный недостаток последовательного подключения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение — это соединение, при котором напряжение на концах участка цепи одинаковое.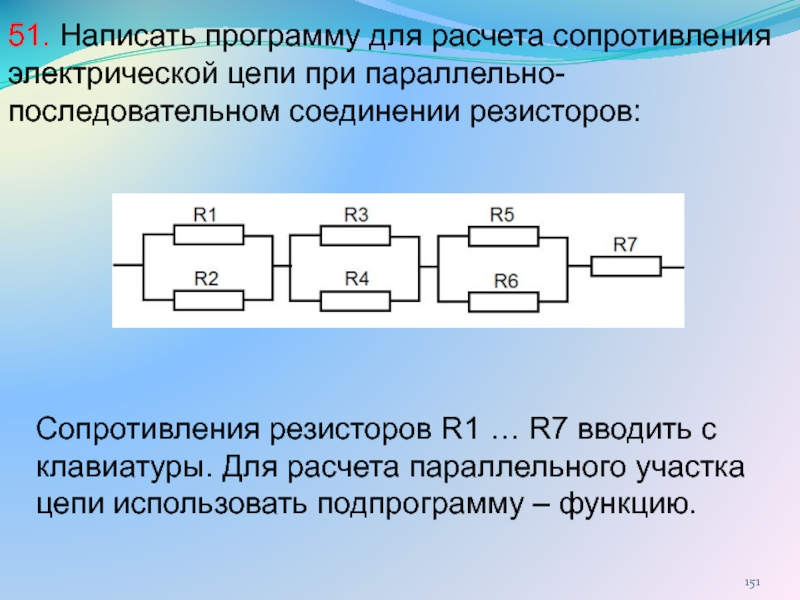 Параллельное соединение является наиболее распространенным, в основном потому, что все элементы находятся под одинаковым напряжением, ток распределяется по-разному, и когда один из элементов уходит, все остальные продолжают свою работу.
Параллельное соединение является наиболее распространенным, в основном потому, что все элементы находятся под одинаковым напряжением, ток распределяется по-разному, и когда один из элементов уходит, все остальные продолжают свою работу.
При параллельном подключении эквивалентное сопротивление находится как
В случае двух параллельно включенных резисторов
В случае трех параллельно включенных резисторов:
Смешанное соединение
Смешанное соединение — соединение, представляющее собой совокупность последовательных и параллельных соединений.Чтобы найти эквивалентное сопротивление, нужно «свернуть» схему, поочередно преобразовывая параллельные и последовательные участки схемы.
Сначала находим эквивалентное сопротивление для параллельного участка цепи, а затем добавляем к нему оставшееся сопротивление R 3. Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 включены последовательно.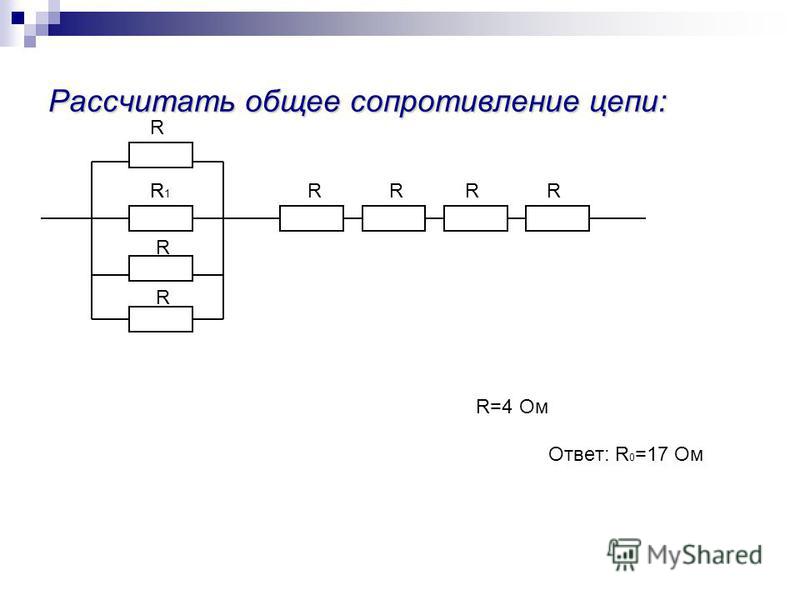
Итак, осталось самое интересное и сложное подключение проводов.
Мостовая схема
Схема подключения моста показана на рисунке ниже.
Чтобы свернуть мостовую схему, один из треугольников моста заменяется эквивалентной звездой.
И найдите сопротивления R 1, R 2 и R 3.
Резисторы
широко используются в электротехнике и электронике. В основном они используются для регулирования в цепях тока и напряжения. Основные параметры: электрическое сопротивление (R) измеряется в Ом, мощность (Вт), стабильность и точность их параметров во время работы.Можно вспомнить еще много его параметров — ведь это обычный промышленный продукт.
Последовательное соединение
Последовательное соединение — это соединение, в котором каждый последующий резистор подключается к предыдущему, образуя непрерывную цепь без разветвлений. Сила тока I = I1 = I2 в такой схеме будет одинаковой в каждой точке. Напротив, напряжение U1, U2 в разных его точках будет различным, а работа по передаче заряда по всей цепи состоит из работы по передаче заряда в каждом из резисторов U = U1 + U2. Напряжение U, согласно закону Ома, равно току, умноженному на сопротивление, и предыдущее выражение можно записать следующим образом:
Напряжение U, согласно закону Ома, равно току, умноженному на сопротивление, и предыдущее выражение можно записать следующим образом:
где R — полное сопротивление цепи. То есть, по-простому, есть падение напряжения в точках соединения резисторов и чем больше подключенных элементов, тем больше происходит падение напряжения
Отсюда следует, что
, общая стоимость такого соединения определяется путем суммирования сопротивлений последовательно. Наши рассуждения справедливы для любого количества последовательно соединенных участков схемы.
Параллельное соединение
Объедините начала нескольких резисторов (точка A). В другой точке (B) соединим все их концы. В результате мы получаем участок схемы, который называется параллельным подключением и состоит из ряда параллельных ветвей (в нашем случае резисторов). В этом случае электрический ток между точками A и B будет распределяться по каждой из этих ветвей.
Напряжения на всех резисторах будут одинаковыми: U = U1 = U2 = U3, их концы — точки A и B.
Заряды, прошедшие через каждый резистор за единицу времени, складываются в заряд, прошедший через весь блок. Следовательно, суммарный ток в цепи, показанной на рисунке, равен I = I1 + I2 + I3.
Теперь, используя закон Ома, последнее равенство преобразуется к такому виду:
U / R = U / R1 + U / R2 + U / R3.
Отсюда следует, что для эквивалентного сопротивления R верно:
1 / R = 1 / R1 + 1 / R2 + 1 / R3
или после преобразования формулы мы можем получить другую запись, например:
.
Чем больше резисторов (или других частей электрической цепи с некоторым сопротивлением) подключено параллельно, тем больше путей для прохождения тока и тем меньше общее сопротивление цепи.
Следует отметить, что величина, обратная сопротивлению, называется проводимостью. Можно сказать, что при параллельном соединении участков схемы складываются проводимости этих участков, а при последовательном соединении — их сопротивления.
Примеры использования
Понятно, что при последовательном включении обрыв цепи в одном месте приводит к тому, что ток перестает течь по всей цепи. Например, елочная гирлянда перестает светиться, если перегорела только одна лампочка, это плохо.
Например, елочная гирлянда перестает светиться, если перегорела только одна лампочка, это плохо.
А вот последовательное соединение лампочек в гирлянду дает возможность использовать большое количество маленьких лампочек, каждая из которых рассчитана на напряжение сети (220 В), деленное на количество лампочек.
Последовательное соединение резисторов на примере 3-х лампочек и ЭДС
Но при последовательном включении предохранительного устройства его срабатывание (разрыв плавкой вставки) позволяет обесточить всю расположенную после него электрическую цепь и обеспечить требуемый уровень безопасности, и это хорошо.Выключатель в блоке питания электроприбора также входит в серию.
Также широко используется параллельное соединение. Например, люстра — все лампочки подключены параллельно и находятся под одинаковым напряжением. Если перегорит одна лампа, это не страшно, остальные не погаснут, они остаются под таким же напряжением.
Параллельное соединение резисторов на примере 3 лампочек и генератора
Когда необходимо увеличить способность схемы рассеивать тепловую мощность, генерируемую протеканием тока, широко используются как последовательные, так и параллельные комбинации резисторов. Как для последовательного, так и для параллельного способов подключения определенного количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Как для последовательного, так и для параллельного способов подключения определенного количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Смешанное соединение резисторов
Также часто используется смешанное соединение. Если, например, необходимо получить сопротивление определенного номинала, но оно недоступно, можно использовать один из вышеперечисленных способов или использовать смешанное подключение.
Отсюда вы можете вывести формулу, которая даст нам требуемое значение:
Rtotal = (R1 * R2 / R1 + R2) + R3
В нашу эпоху развития электроники и различных технических устройств все сложности основаны на простых законах, которые поверхностно рассмотрены на этом сайте и я думаю, что они помогут вам успешно применить их в своей жизни.Если, например, взять гирлянду на елку, то соединения лампочек следуют друг за другом, т.е. грубо говоря это отдельное сопротивление.
Не так давно гирлянды стали соединять смешанным способом.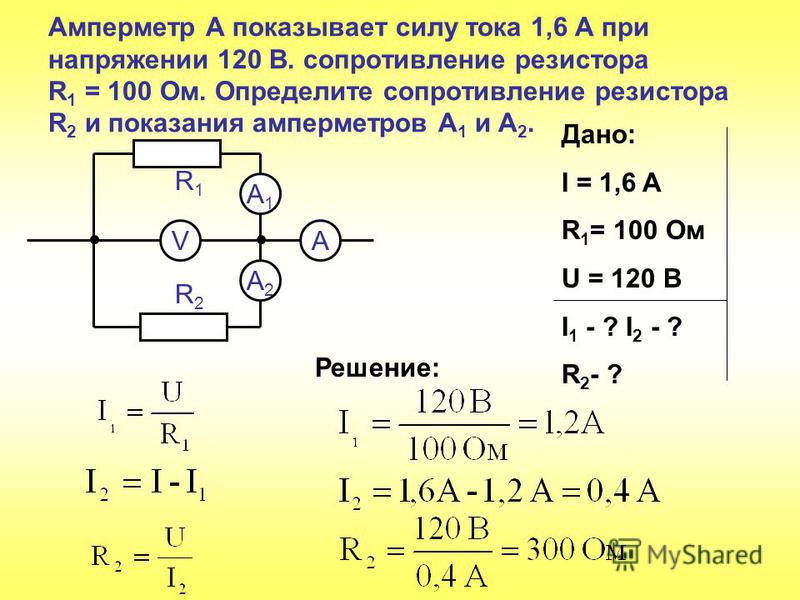 Вообще, в совокупности все эти примеры с резисторами взяты условно, т.е. любой резистивный элемент может быть током, проходящим через элемент с падением напряжения и тепловыделением.
Вообще, в совокупности все эти примеры с резисторами взяты условно, т.е. любой резистивный элемент может быть током, проходящим через элемент с падением напряжения и тепловыделением.
Возьмите три постоянных сопротивления R1, R2 и R3 и включите их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R. 3, а к началу первого сопротивления и к концу третьего подводим проводники от источника тока (рис.1).
Это соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет одинаковым во всех ее точках.
Рис 1
Как определить полное сопротивление цепи, если мы уже знаем все сопротивления, включенные в нее последовательно? Используя положение, что напряжение U на выводах источника тока равно сумме падений напряжения на участках цепи, можно записать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
ИК = ИК1 + ИК2 + ИК3
Вынимая I из скобок в правой части равенства, получаем IR = I (R1 + R2 + R3).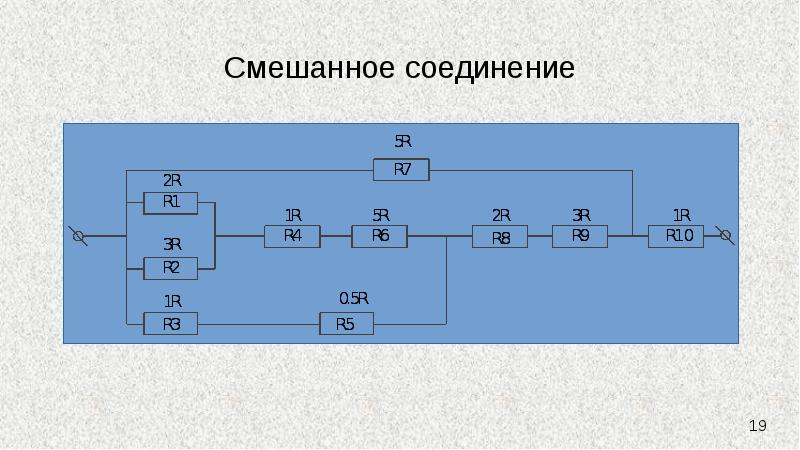
Разделив теперь обе части равенства на I, окончательно имеем R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Давайте проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, значения которых известны (например, R1 = = 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом).Соединяем их последовательно (рис. 2) и подключаем к источнику тока, ЭДС которого составляет 60 В (в пренебрежении).
Рис. 2. Пример последовательного соединения трех сопротивлений
Давайте посчитаем, какие показания должны давать включенные устройства, как показано на схеме, если замкнуть цепь. Определите внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдите ток в цепи: 60/80 = 0,75 А
Зная ток в цепи и сопротивление ее участков, определяем падение напряжения на каждом участке цепи U 1 = 0.75 х 10 = 7,5 В, U 2 = 0,75 х 20 = 15 В, U3 = 0,75 х 50 = 37,5 Б.
Зная падение напряжения на участках, определяем полное падение напряжения во внешней цепи, т.е. напряжение на выводах источника тока U = 7,5 + 15 + 37,5 = 60 В.
Получили таким образом, что U = 60 В, т.е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Теперь, замкнув ключевой выключатель K, можно по приборам убедиться, что наши расчеты приблизительно верны.
Возьмите два постоянных сопротивления R1 и R2 и соедините их так, чтобы истоки этих сопротивлений находились в одной общей точке a, а концы — в другой общей точке b. Соединив затем точки a и b с источником тока, мы получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим, как протекает ток в этой цепи. От положительного полюса источника тока через соединительный проводник ток достигнет точки а. В точке a он разветвляется, так как здесь сама цепь разветвляется на две отдельные ветви: первая ветвь с сопротивлением R1 и вторая с сопротивлением R2. Обозначим токи в этих ветвях через I1 и I2 соответственно.Каждый из этих токов пойдет своей веткой до точки b. В этот момент токи сольются в один общий ток, который подойдет к отрицательному полюсу источника тока.
В точке a он разветвляется, так как здесь сама цепь разветвляется на две отдельные ветви: первая ветвь с сопротивлением R1 и вторая с сопротивлением R2. Обозначим токи в этих ветвях через I1 и I2 соответственно.Каждый из этих токов пойдет своей веткой до точки b. В этот момент токи сольются в один общий ток, который подойдет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, каким будет соотношение токов в составленной нами схеме.
Включите амперметр между положительным полюсом источника тока (+) и точкой a и запишите его показания. Затем включив амперметр (показан на рисунке пунктирной линией) в точке соединения провода b с отрицательным полюсом источника тока (-), заметим, что прибор покажет такую же силу тока.
Это означает, что до его разветвления (до точки а) сила тока равна силе тока после разветвления цепи (после точки б).
Теперь по очереди включим амперметр в каждой ветви цепи, запоминая показания прибора. Пусть амперметр в первой ветви показывает силу тока I1, а во второй — I 2. Складывая эти два показания амперметра, получаем полный ток, равный по величине току I до разветвления (до точки а) .
Пусть амперметр в первой ветви показывает силу тока I1, а во второй — I 2. Складывая эти два показания амперметра, получаем полный ток, равный по величине току I до разветвления (до точки а) .
Следовательно, сила тока, протекающего в точке разветвления, равна сумме сил токов, протекающих из этой точки.I = I1 + I2 Выражая это формулой, получаем
Это соотношение, имеющее большое практическое значение, называется законом разветвленной цепи.
Давайте теперь посмотрим, какое будет соотношение между токами в ветвях.
Давайте включим вольтметр между точками a и b и посмотрим, что он нам показывает. Сначала вольтметр покажет напряжение источника тока, поскольку он подключен, как видно из рис. 3, непосредственно к клеммам источника тока.Во-вторых, вольтметр покажет падения напряжения U1 и U2 на сопротивлениях R1 и R2, поскольку он подключен к началу и концу каждого сопротивления.
Следовательно, когда сопротивления соединены параллельно, напряжение на выводах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право писать, что U = U1 = U2,
где U — напряжение на выводах источника тока; U1 — падение напряжения на сопротивлении R1, U2 — падение напряжения на сопротивлении R2.Напомним, что падение напряжения на участке цепи численно равно произведению тока, протекающего через этот участок, на сопротивление участка U = IR.
Следовательно, для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2, но так как U1 = U2, то I1R1 = I2R2.
Применяя к этому выражению правило пропорциональности, получаем I1 / I2 = U2 / U1, т.е. ток в первой ветви будет во столько раз больше (или меньше), чем ток во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные значениям сопротивления параллельных ветвей. Другими словами, чем больше сопротивление ветви, тем меньше тока будет протекать через нее, и, наоборот, чем меньше сопротивление ветви, тем больше тока будет течь через эту ветвь.
Проверим правильность этой зависимости на следующем примере.Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Давайте сначала посчитаем, что нам покажет амперметр, включенный в каждую ветку:
I1 = U / R1 = 3/10 = 0,3 А = 300 мА
I 2 = U / R 2 = 3/20 = 0,15 А = 150 мА
Суммарный ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Наш расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи ответвляется обратно пропорционально сопротивлениям.
Действительно, R1 = 10 Ом — это половина размера R 2 = 20 Ом, а I1 = 300 мА — вдвое больше, чем I2 = 150 мА. Суммарный ток в цепи I = 450 мА разветвился на две части так, чтобы большая его часть (I1 = 300 мА) прошла через меньшее сопротивление (R1 = 10 Ом), а меньшую часть (R2 = 150 мА). ) через большее сопротивление (R 2 = 20 Ом).
Это разветвление тока по параллельным ветвям аналогично течению жидкости по трубам. Представьте трубу A, которая в какой-то момент разветвляется на две трубы B и C разного диаметра (рис. 4). Поскольку диаметр трубы B больше диаметра трубы C, через трубу B одновременно пройдет больше воды, чем через трубу C, которая имеет большее сопротивление потоку воды.
Представьте трубу A, которая в какой-то момент разветвляется на две трубы B и C разного диаметра (рис. 4). Поскольку диаметр трубы B больше диаметра трубы C, через трубу B одновременно пройдет больше воды, чем через трубу C, которая имеет большее сопротивление потоку воды.
Рис.4
Давайте теперь посмотрим, каким будет полное сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи следует понимать такое сопротивление, которое может заменить оба параллельно соединенных сопротивления при заданном напряжении цепи без изменения тока перед разветвлением.Это сопротивление называется эквивалентным сопротивлением.
Вернемся к схеме, показанной на рис. 3 и посмотрите, каким будет эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применив к этой схеме закон Ома, можно записать: I = U / R, где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи. внешняя цепь, то есть эквивалентное сопротивление.
внешняя цепь, то есть эквивалентное сопротивление.
Таким же образом для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I 2 — токи в ответвлениях; U1 и U2 — напряжение ветви; R1 и R2 — сопротивления ответвления.
Разветвленная цепь: I = I1 + I2
Подставляя значения токов, получаем U / R = U1 / R1 + U2 / R2
Так как при параллельном включении U = U1 = U2, то можно записать U / R = U / R1 + U / R2
Вынося U в правой части равенства за скобки, получаем U / R = U (1 / R1 + 1 / R2)
Разделив теперь обе части равенства на U, окончательно имеем 1 / R = 1 / R1 + 1 / R2
Помня, что проводимость обратно пропорциональна сопротивлению, мы можем сказать, что в полученной формуле 1 / R — проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2 — проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном подключении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление параллельно включенных сопротивлений, необходимо определить проводимость цепи и принять значение, противоположное ей.
Из формулы также следует, что проводимость цепи больше, чем проводимость каждой ветви, а это означает, что эквивалентное сопротивление внешней цепи меньше наименьшего из сопротивлений, соединенных параллельно.
Рассматривая случай параллельного соединения сопротивлений, мы взяли простейшую схему, состоящую из двух ветвей. Однако на практике могут быть случаи, когда цепочка состоит из трех и более параллельных ветвей. Как действовать в этих случаях?
Оказывается, все полученные нами соотношения остаются в силе для цепи, состоящей из любого количества параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмите три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соедините их параллельно. Определите эквивалентное сопротивление цепи (рис. 5).
Рис. 5. Схема с тремя параллельно включенными сопротивлениями
Применяя для этой цепочки формулу 1 / R = 1 / R1 + 1 / R2, можно записать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставив известные значения, получим 1 / R = 1/10 + 1/20 + 1/60
Складываем эти дроби: 1 / R = 10/60 = 1/6, то есть проводимость цепи 1 / R = 1/6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего сопротивления, включенного параллельно в цепи, т.е. меньше сопротивления R1.
Давайте теперь посмотрим, действительно ли это сопротивление эквивалентно, то есть таким, чтобы оно могло заменить сопротивления 10, 20 и 60 Ом, соединенные параллельно, без изменения силы тока перед разветвлением цепи.
Предположим, что напряжение внешней цепи и, следовательно, напряжение на сопротивлениях R1, R2, R3 равно 12 В.Тогда сила токов в ответвлениях будет: I1 = U / R1 = 12/10 = 1, 2 AI 2 = U / R 2 = 12/20 = 1,6 AI 3 = U / R1 = 12/60 = 0,2 А
Получаем полный ток в цепи по формуле I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим, используя формулу закона Ома, получится ли в цепи ток 2 А, если вместо трех известных нам параллельно соединенных сопротивлений включить одно эквивалентное сопротивление 6 Ом.
I = U / R = 12/6 = 2 А
Как видите, найденное нами сопротивление R = 6 Ом действительно эквивалентно для этой схемы.
Это можно проверить на измерительных приборах, если вы соберете цепь с такими сопротивлениями, которые мы взяли, измерили ток во внешней цепи (перед разветвлением), затем заменили параллельно соединенные сопротивления одним сопротивлением 6 Ом и снова измерили ток. . Показания амперметра в обоих случаях будут примерно одинаковыми.
На практике также могут возникать параллельные соединения, для которых легче вычислить эквивалентное сопротивление, то есть без предварительного определения проводимости сразу найти сопротивление.
Например, если два сопротивления R1 и R2 соединены параллельно, то формула 1 / R = 1 / R1 + 1 / R2 может быть преобразована следующим образом: 1 / R = (R2 + R1) / R1 R2 и , решив равенство по R, получим R = R1 x R2 / (R1 + R2), т.е. при параллельном соединении двух сопротивлений сопротивление эквивалентной схемы равно произведению параллельно соединенных сопротивлений, деленному на их сумма.
2 параллельное соединение проводов.
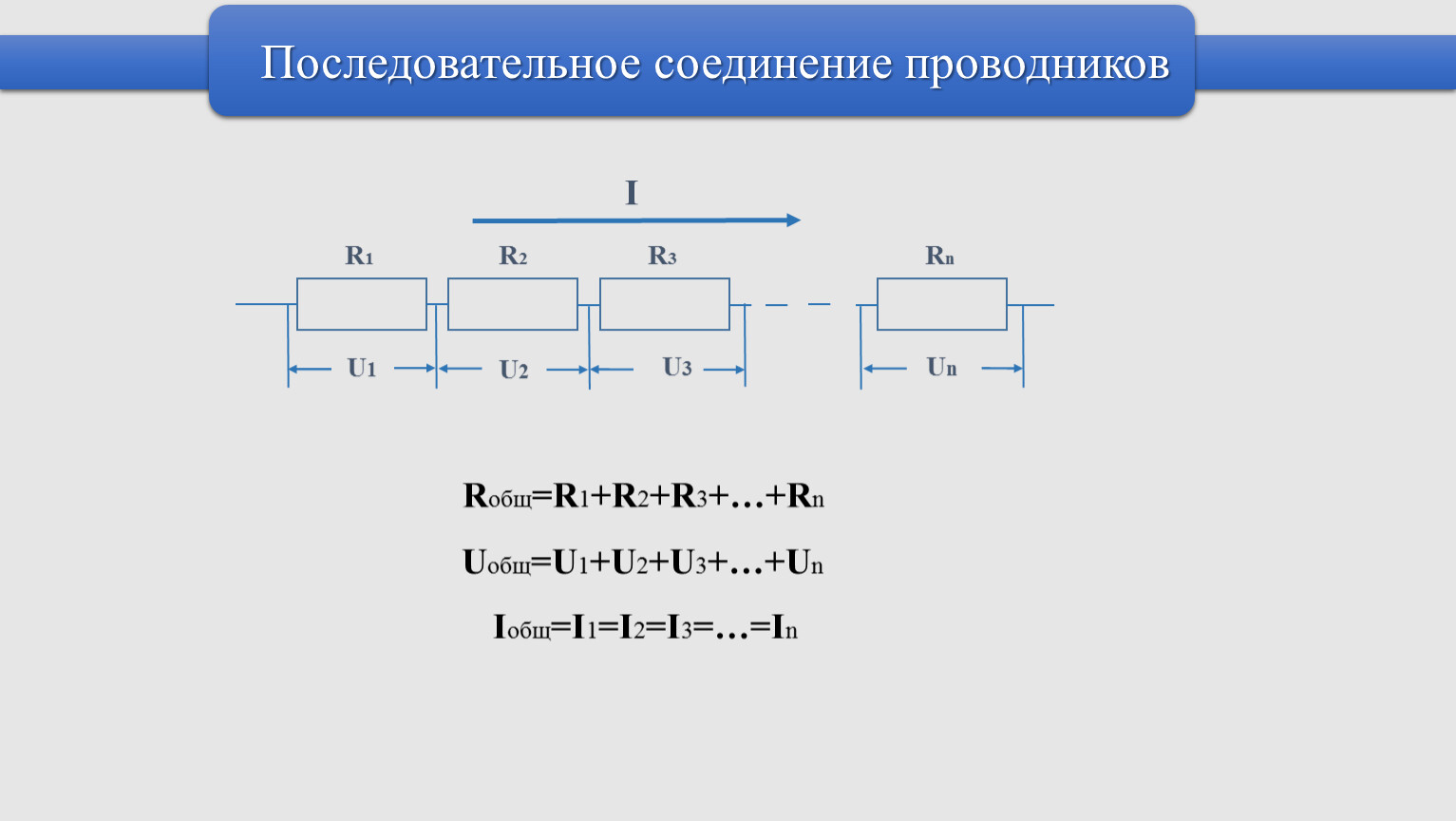 Ток проводника при параллельном и последовательном соединении
Ток проводника при параллельном и последовательном соединении
1. Найдите эквивалентное сопротивление участков цепи при параллельном включении резисторов. Рисунок 2. Последовательное соединение резисторов. Чтобы рассчитать сопротивление таких соединений, вся схема разбивается на простейшие участки, из параллельно или последовательно соединенных резисторов.
Этот результат следует из того факта, что заряды не могут накапливаться в точках разветвления тока (узлы A и B) в цепи постоянного тока.Этот результат действителен для любого количества параллельно соединенных проводов.
На рис. 1.9.3 показывает пример такой сложной цепочки и показывает последовательность вычислений. Следует отметить, что не все сложные схемы, состоящие из проводов с разным сопротивлением, можно рассчитать по формулам для последовательного и параллельного включения.
Когда проводники соединены последовательно, ток во всех проводниках одинаков. При параллельном подключении падение напряжения между двумя узлами, соединяющими элементы схемы, одинаково для всех элементов.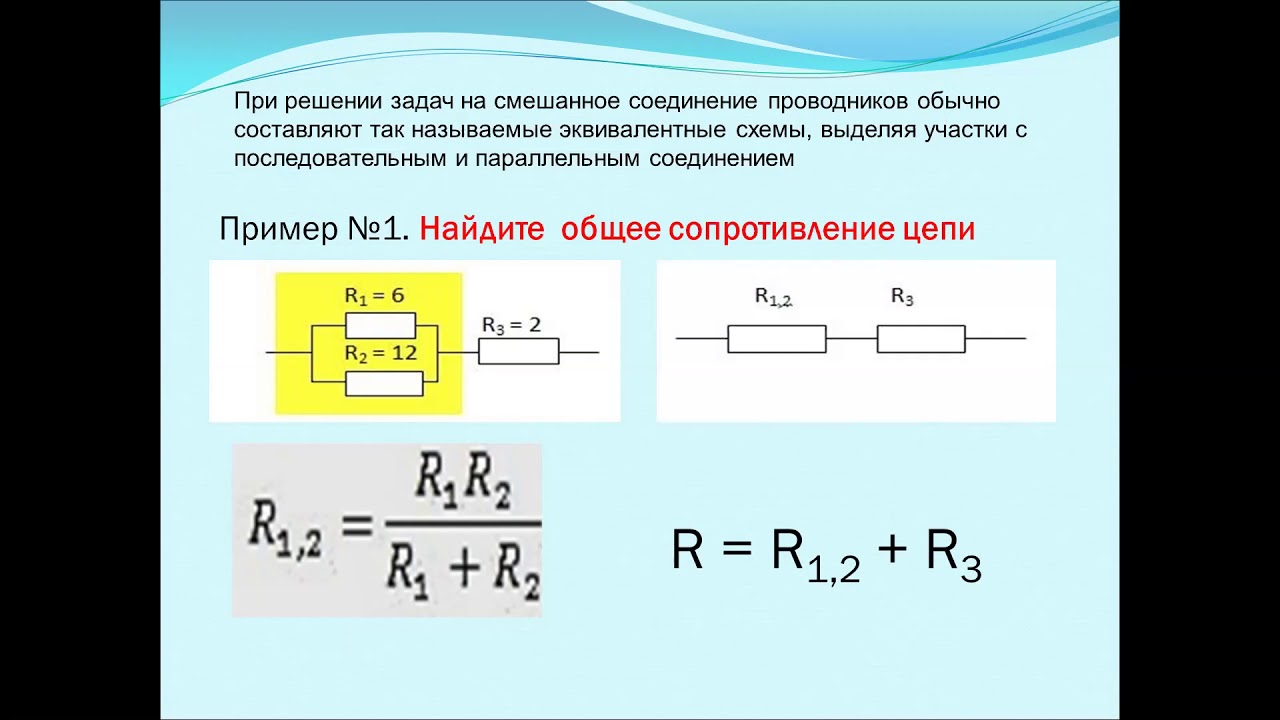
То есть чем больше сопротивление резистора, тем больше на нем падает напряжение. В результате к одной точке (электрическому узлу) можно подключить несколько резисторов. При таком подключении через каждый резистор будет протекать отдельный ток. Сила этого тока будет обратно пропорциональна сопротивлению резистора.
Таким образом, при параллельном подключении резисторов с разным сопротивлением общее сопротивление всегда будет меньше, чем значение наименьшего отдельного резистора.Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и падением напряжения на каждом резисторе в отдельности. Смешанное соединение — это участок цепи, в котором некоторые резисторы включены последовательно, а некоторые — параллельно.
Цепь разделена на секции с только параллельным или только последовательным подключением. Рассчитайте общее сопротивление для каждой отдельной секции. Рассчитайте общее сопротивление для всей схемы смешанного подключения. Существует также более быстрый способ рассчитать полное сопротивление для смешанного соединения. Если резисторы включены последовательно — доп.
Существует также более быстрый способ рассчитать полное сопротивление для смешанного соединения. Если резисторы включены последовательно — доп.
То есть при последовательном соединении резисторы будут подключаться друг за другом. На рисунке 4 показан простейший пример подключения смешанного резистора. После расчета эквивалентных сопротивлений резисторов схема перерисовывается. Обычно цепь получается из последовательно соединенных эквивалентных сопротивлений. 4. Рисунок 5. Расчет сопротивления участка цепи при смешанном включении резисторов.
В результате вы научитесь с нуля не только разрабатывать собственные устройства, но и сопрягать с ними различные периферийные устройства! Узел — это точка разветвления цепи, в которой соединено не менее трех проводников. Для увеличения сопротивления используется последовательное соединение резисторов.
Параллельное напряжение
Как видите, гораздо удобнее рассчитывать сопротивление двух параллельных резисторов. Параллельное соединение резисторов часто используется в случаях, когда требуется более высокое сопротивление мощности.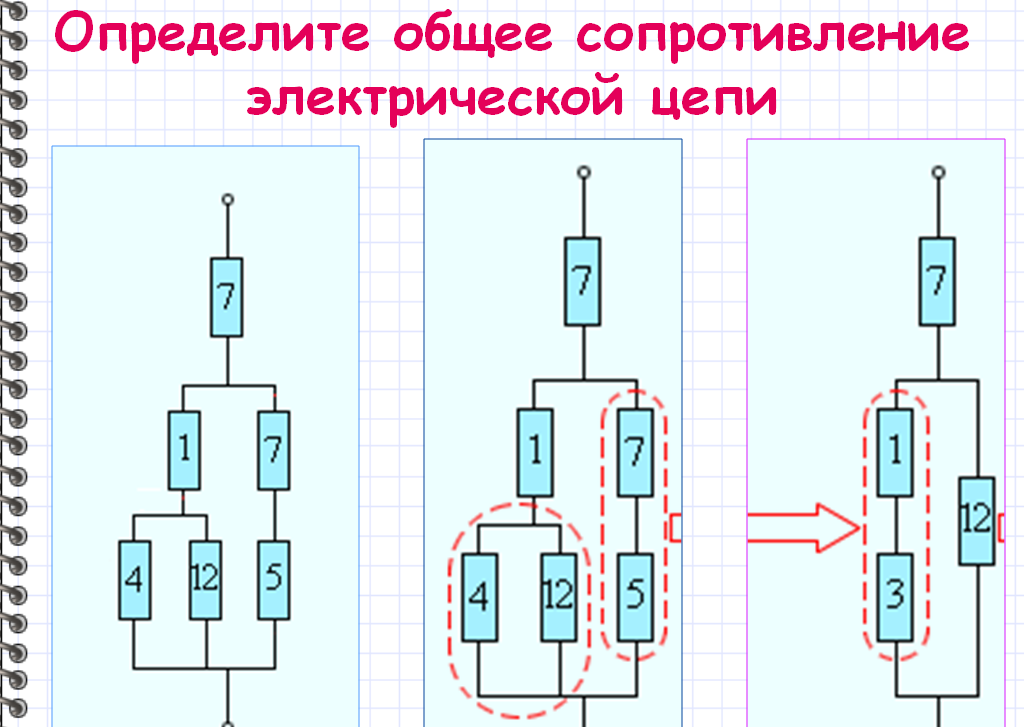 Для этого, как правило, используются резисторы одинаковой мощности и одинакового сопротивления.
Для этого, как правило, используются резисторы одинаковой мощности и одинакового сопротивления.
Общее сопротивление Rtot
Это соединение сопротивлений называется последовательным. Получили таким образом, что U = 60 В, т.е. несуществующее равенство ЭДС источника тока и его напряжения. Теперь мы включим амперметр по очереди в каждой ветви цепи, запоминая показания прибора. Следовательно, когда сопротивления соединены параллельно, напряжение на выводах источника тока равно падению напряжения на каждом сопротивлении.
Это разветвление тока по параллельным ветвям аналогично течению жидкости по трубам. Давайте теперь посмотрим, каким будет полное сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Вернемся к схеме, показанной на рис. 3 и посмотрите, каким будет эквивалентное сопротивление двух параллельно соединенных сопротивлений. Таким же образом для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение ветви; R1 и R2 — сопротивления ответвления.
Это означает, что общее сопротивление цепи всегда будет ниже, чем у любого резистора, подключенного параллельно. 2. Если в этих секциях есть последовательно включенные резисторы, сначала рассчитайте их сопротивление. Применяя закон Ома к участку цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.
Необходимо рассчитать сопротивление последовательных, параллельных или комбинированных цепей? Нужен, если не хочешь сжечь доску! Эта статья покажет вам, как это сделать.Перед чтением следует понимать, что у резисторов нет «начала» и «конца». Эти слова введены для облегчения понимания представленного материала.
ступеньки
Последовательное сопротивление
Сопротивление параллельной цепи
Комбинированное сопротивление
Некоторые факты
- Каждый электропроводящий материал имеет некоторое сопротивление, то есть сопротивление материала электрическому току.

- Сопротивление измеряется в Ом.Символ единицы измерения Ом — Ω.
- Различные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0,0000017 Ом / см 3
- Сопротивление керамики около 10 14 Ом / см 3
- Чем выше значение сопротивления, тем выше сопротивление электрическому току. Медь, которая часто используется в электрических проводах, имеет очень небольшое сопротивление. С другой стороны, сопротивление керамики очень высокое, что делает ее отличным изолятором.
- Работа всей схемы зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
- U = IR. Это закон Ома, установленный Георгом Омом в начале 1800-х годов. Если вам даны какие-либо две из этих переменных, вы легко найдете третью.
- U = IR: Напряжение (U) — это произведение тока (I) * на сопротивление (R).
- I = U / R: Ток является отношением напряжения (U) к сопротивлению (R).
- R = U / I: Сопротивление — это отношение напряжения (U) к току (I).

- Помните: при параллельном подключении есть несколько путей для прохождения тока через цепь, поэтому в такой цепи общее сопротивление будет меньше, чем сопротивление каждого отдельного резистора. При последовательном соединении ток течет через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
- Общее сопротивление в параллельной цепи всегда меньше, чем сопротивление одного резистора с наименьшим сопротивлением в этой цепи.Общее сопротивление в последовательной цепи всегда больше, чем сопротивление одного резистора с наибольшим сопротивлением в этой цепи.
Один из китов, на котором держатся многие концепции в электронике, — это концепция последовательного и параллельного соединения проводников. Просто необходимо знать основные отличия этих типов подключения. Без этого невозможно понять и прочитать ни одну диаграмму.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве жилы выбирают медный кабель. Это связано с требованием к проводнику: он должен легко выделять электроны.
Чаще всего в качестве жилы выбирают медный кабель. Это связано с требованием к проводнику: он должен легко выделять электроны.
Независимо от способа подключения электрический ток идет с плюса на минус. Именно в этом направлении потенциал уменьшается. При этом стоит помнить, что провод, по которому протекает ток, тоже имеет сопротивление. Но значение его очень невелико. Вот почему им пренебрегают. Сопротивление проводника принимается равным нулю.В том случае, если проводник имеет сопротивление, его принято называть резистором.
Параллельное соединение
В этом случае элементы, входящие в цепочку, соединяются между собой двумя узлами. У них нет связи с другими узлами. Участки цепочки с таким соединением принято называть ответвлениями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в этом случае все проводники соединяются одним концом в одном узле, а вторым — во втором.Это приводит к тому, что электрический ток разделяется на все элементы. Это увеличивает проводимость всей цепи.
Это увеличивает проводимость всей цепи.
При таком подключении проводов к цепи напряжение на каждом из них будет одинаковым. Но сила тока всей цепи будет определяться как сумма токов, протекающих через все элементы. Принимая во внимание закон Ома, с помощью простых математических расчетов получается интересная картина: величина, обратная величине полного сопротивления всей цепи, определяется как сумма значений, обратных сопротивлениям каждого отдельного элемента.В этом случае учитываются только элементы, соединенные параллельно.
Последовательное соединение
В этом случае все элементы цепочки соединены таким образом, что они не образуют единого узла. У такого способа подключения есть один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы не смогут работать. Яркий пример такой ситуации — обычная гирлянда. Если в нем перегорит одна из лампочек, то перестает работать вся гирлянда.
Последовательное соединение элементов отличается тем, что сила тока во всех проводниках одинакова. Что касается напряжения цепи, то оно равно сумме напряжений отдельных элементов.
Что касается напряжения цепи, то оно равно сумме напряжений отдельных элементов.
В этой схеме жилы включены в цепь поочередно. Это означает, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть полное сопротивление цепи равно сумме сопротивлений всех проводников.Эту же зависимость можно получить математически, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное соединение элементов. В этом случае говорят о смешанной связи. Расчет таких схем проводится отдельно для каждой группы проводников.
Итак, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, соединенных параллельно, и сопротивление элементов, соединенных последовательно.В этом случае последовательное соединение является доминирующим. То есть рассчитывается в первую очередь. И только после этого определяется сопротивление элементов при параллельном включении.
Подключение светодиодов
Зная основы двух типов соединительных элементов в цепи, вы можете понять принцип построения схем различных электроприборов. Давайте посмотрим на пример. во многом зависит от напряжения источника тока.
При низком сетевом напряжении (до 5 В) светодиоды включаются последовательно.В этом случае сквозной конденсатор и линейные резисторы помогут снизить уровень электромагнитных помех. Электропроводность светодиодов увеличена за счет использования системных модуляторов.
При напряжении сети 12 В можно использовать как последовательную, так и параллельную сеть. В случае последовательного подключения используются импульсные блоки питания. Если собрать цепочку из трех светодиодов, то можно обойтись без усилителя. Но если в схему будет входить больше элементов, то потребуется усилитель.
Во втором случае, то есть при параллельном подключении, необходимо использовать два открытых резистора и усилитель (с полосой пропускания более 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком сетевом напряжении (220 В) используется последовательное соединение. В этом случае дополнительно используются операционные усилители и понижающие блоки питания.
Содержимое:
Ток в электрической цепи осуществляется по проводникам, по направлению от источника к потребителям.В большинстве этих схем используются медные провода и электрические приемники в определенном количестве с разным сопротивлением. В зависимости от выполняемых задач в электрических схемах используется последовательное и параллельное соединение проводов. В некоторых случаях могут применяться оба типа подключений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их необходимо заранее учитывать при проектировании схем, ремонте и обслуживании электрооборудования.
Последовательное соединение проводов
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводов, предполагающая одинаковое подключение потребителей. В этом случае подключение к схеме осуществляется по очереди в порядке приоритета. То есть начало одного потребителя подключается к концу другого с помощью проводов, без каких-либо ответвлений.
Среди них часто используется схема последовательного соединения проводов, предполагающая одинаковое подключение потребителей. В этом случае подключение к схеме осуществляется по очереди в порядке приоритета. То есть начало одного потребителя подключается к концу другого с помощью проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Сила тока, напряжение и сопротивление на каждом из них следует обозначить соответственно как I1, U1, R1 и I2, U2, R2.В результате были получены соотношения, выражающие соотношение между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются на практике проведением измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение жил имеет следующие индивидуальные характеристики:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи — это сумма напряжений в каждой секции.

- Общее сопротивление включает сопротивление каждого отдельного проводника.
Эти соотношения подходят для любого количества последовательно соединенных проводов. Общее значение сопротивления всегда выше, чем сопротивление любого отдельного проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит к увеличению сопротивления.
Если вы соедините последовательно одинаковые элементы в количестве n, вы получите R = n x R1, где R — полное сопротивление, R1 — сопротивление одного элемента, а n — количество элементов.Напряжение U, напротив, делится на равные части, каждая из которых в n раз меньше суммарного значения. Например, если 10 ламп одинаковой мощности подключены последовательно к сети с напряжением 220 вольт, то напряжение в любой из них будет: U1 = U / 10 = 22 вольта.
Последовательно соединенные проводники имеют отличительную особенность. Если хотя бы один из них выходит из строя во время работы, то ток прекращается по всей цепи.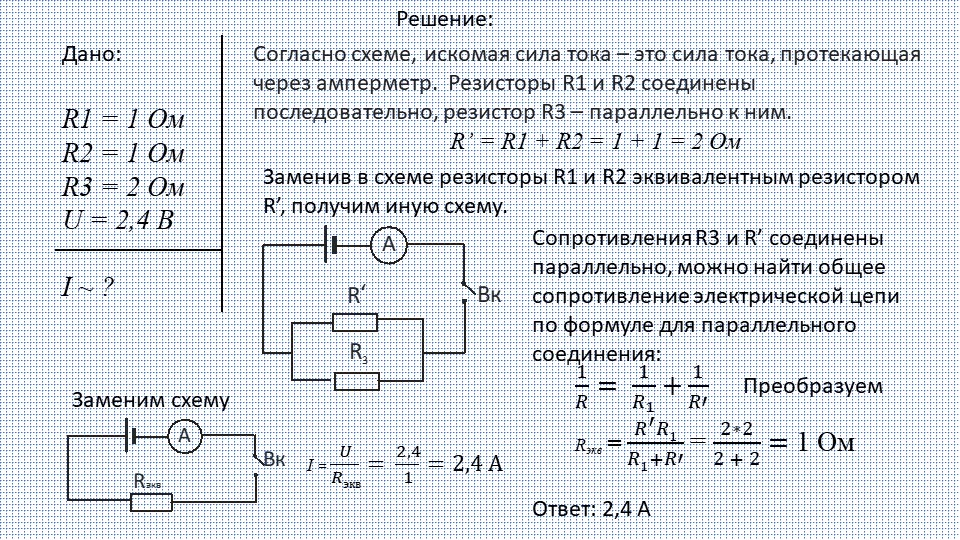 Самый яркий пример — когда перегоревшая лампочка в последовательной цепи приводит к выходу из строя всей системы.Чтобы установить перегоревшую лампочку, потребуется проверить всю гирлянду.
Самый яркий пример — когда перегоревшая лампочка в последовательной цепи приводит к выходу из строя всей системы.Чтобы установить перегоревшую лампочку, потребуется проверить всю гирлянду.
Параллельное соединение проводов
В электрических сетях проводники могут быть соединены различными способами: последовательно, параллельно и в комбинации. Среди них параллельное соединение — такой вариант, когда проводники в начальной и конечной точках соединяются между собой. Таким образом, начало и конец нагрузок соединяются между собой, а сами нагрузки располагаются параллельно друг другу.Электрическая цепь может содержать два, три или более проводников, соединенных параллельно.
Если мы рассматриваем последовательное и параллельное соединение, силу тока в последней версии можно исследовать с помощью следующей диаграммы. Возьмите две лампы накаливания с одинаковым сопротивлением, соединенные параллельно. Для управления каждая лампочка подключена к своей. Кроме того, используется еще один амперметр для контроля общего тока в цепи. Схема тестирования дополнена блоком питания и ключом.
Схема тестирования дополнена блоком питания и ключом.
После закрытия ключа нужно следить за показаниями средств измерений. Амперметр на лампе №1 покажет силу тока I1, а на лампе №2 — силу тока I2. Обычный амперметр показывает значение силы тока, равное сумме токов отдельных, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного подключения, если одна из лампочек перегорит, другая будет работать нормально. Поэтому в домашних электрических сетях используется параллельное соединение устройств.
Используя ту же схему, можно установить значение эквивалентного сопротивления. Для этого в электрическую цепь добавляется вольтметр. Это позволяет измерять напряжение при параллельном подключении, при этом сила тока остается прежней. Также есть точки пересечения проводников, соединяющих обе лампы.
В результате измерений полное напряжение при параллельном включении будет: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменив все элементы в этой схеме. При параллельном подключении в соответствии с законом Ома I = U / R получается следующая формула: U / R = U1 / R1 + U2 / R2, в которой R — эквивалентное сопротивление, R1 и R2 — сопротивления обоих лампочки, U = U1 = U2 — значение напряжения, показываемое вольтметром.
При параллельном подключении в соответствии с законом Ома I = U / R получается следующая формула: U / R = U1 / R1 + U2 / R2, в которой R — эквивалентное сопротивление, R1 и R2 — сопротивления обоих лампочки, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Также следует принять во внимание, что токи в каждой цепи в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление, будет выглядеть так: 1 / R = 1 / R1 + 1 / R2.С увеличением количества элементов в таких цепочках количество слагаемых в формуле также увеличивается. Разница в основных параметрах отличает друг от друга и источники тока, что позволяет использовать их в различных электрических цепях.
Параллельное соединение проводов характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет относительно высокой. Этот фактор следует учитывать при включении в розетки большого количества электроприборов.В этом случае сила тока значительно увеличивается, что приводит к перегреву кабельных линий и последующим пожарам.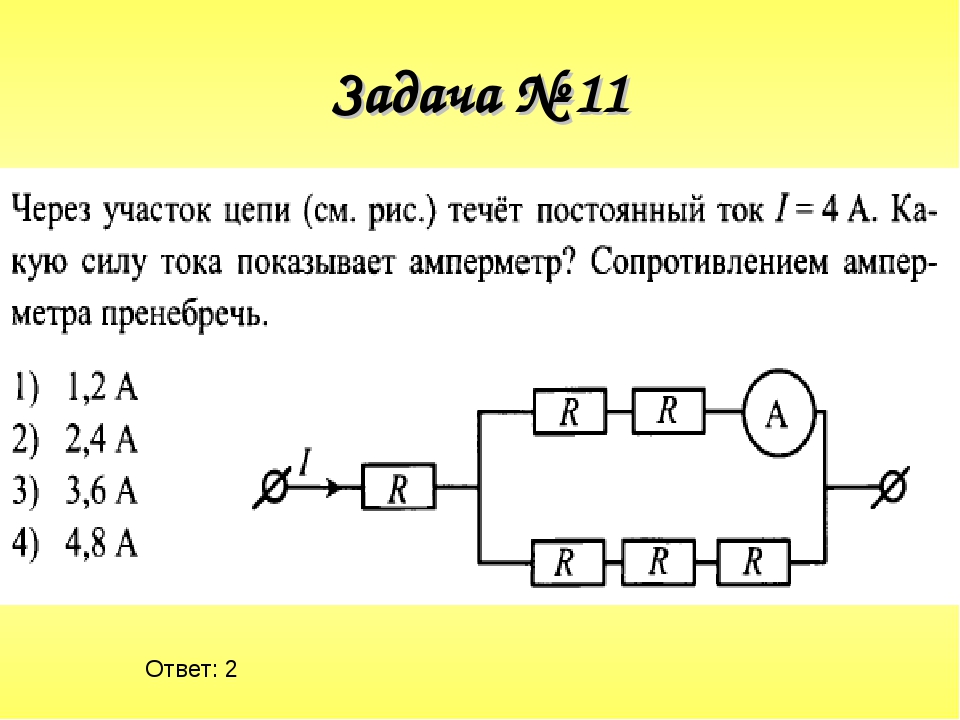
Правила последовательного и параллельного соединения проводов
Эти законы, касающиеся обоих типов присоединения проводов, уже частично учитывались ранее.
Для более четкого понимания и восприятия в практической плоскости последовательного и параллельного соединения проводников формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводе: I = I1 = I2.
- параллельное и последовательное соединение проводов объясняется в каждом случае по-своему. Например, при последовательном подключении напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение складывается из напряжений каждого проводника: U = U1 + U2 = I (R1 + R2) = IR.
- Общее сопротивление цепи при последовательном соединении складывается из суммы сопротивлений всех отдельных проводников, независимо от их количества.

- При параллельном включении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Полный ток, измеренный во всей цепи, равен сумме токов, протекающих через все проводники, соединенные параллельно друг другу: I = I1 + I2.
Чтобы более эффективно проектировать электрические сети, необходимо хорошо знать последовательное и параллельное соединение проводов и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводов
В электрических сетях, как правило, используется последовательное параллельное и смешанное соединение проводов, рассчитанное на определенные условия эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, который представляет собой набор комбинаций, состоящих из разных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которого обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельных резисторов, но и из довольно сложных участков, включающих множество элементов.
Эти соединения состоят не только из отдельных резисторов, но и из довольно сложных участков, включающих множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета состоит в разбиении схемы на более простые компоненты, которые считаются отдельно, а затем суммируются друг с другом.
Согласованным такое соединение резисторов называется, когда конец одного проводника соединяется с началом другого и т. Д.(рисунок 1). При последовательном включении сила тока в любой части электрической цепи одинакова. Это связано с тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля и, как следствие, к изменению силы тока. Вот почему
Амперметр A измеряет ток в цепи и имеет низкое внутреннее сопротивление (R A 0).
Входящие в комплект вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2. Вольтметр V измеряет напряжение U, подаваемое на клеммы M и N. Вольтметры показывают, что при последовательном включении напряжение U равно сумме напряжений на отдельных участках цепи:
Вольтметр V измеряет напряжение U, подаваемое на клеммы M и N. Вольтметры показывают, что при последовательном включении напряжение U равно сумме напряжений на отдельных участках цепи:
Применяя закон Ома для каждого участка схемы, получаем:
где R — полное сопротивление последовательно соединенной цепи. Подставляя U, U 1, U 2 в формулу (1), получаем
Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:
Если сопротивления отдельных резисторы равны между собой, т.е.е. R 1 = R 2 = … = R n, тогда общее сопротивление этих резисторов при последовательном включении в n раз больше, чем сопротивление одного резистора: R = nR 1.
При последовательном соединении резисторов следующие отношение верно
тех. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узел — это точка в разветвленной цепи, где сходятся более двух проводников. При параллельном соединении резисторов к точкам M и N подключают вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это связано с тем, что работа сил стационарного электрического поля не зависит от формы траектории:
2). Узел — это точка в разветвленной цепи, где сходятся более двух проводников. При параллельном соединении резисторов к точкам M и N подключают вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это связано с тем, что работа сил стационарного электрического поля не зависит от формы траектории:
Амперметр показывает, что ток I в неразветвленной части цепи равен сумме токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:
Это также следует из закона сохранения электрического заряда.Применяем закон Ома к отдельным участкам цепи и всей цепи с общим сопротивлением R:
Подставляя I, I 1 и I 2 в формулу (2), получаем.
.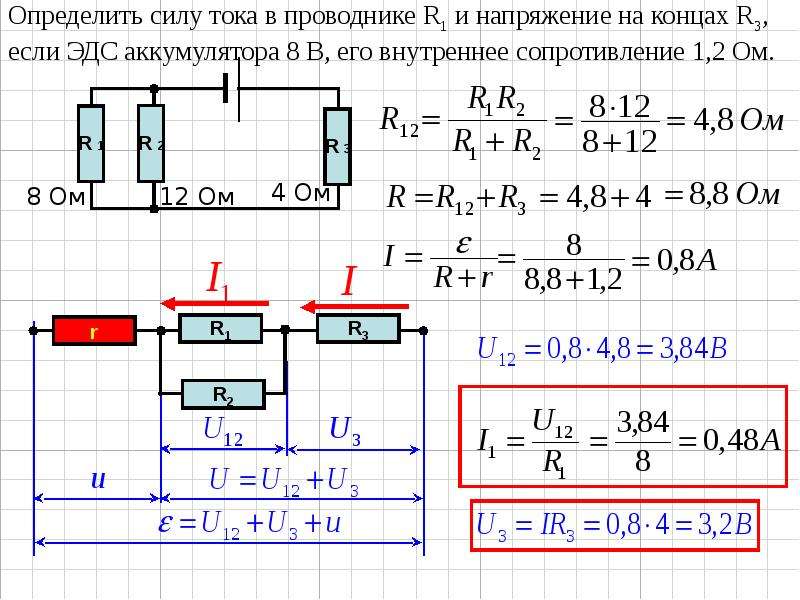


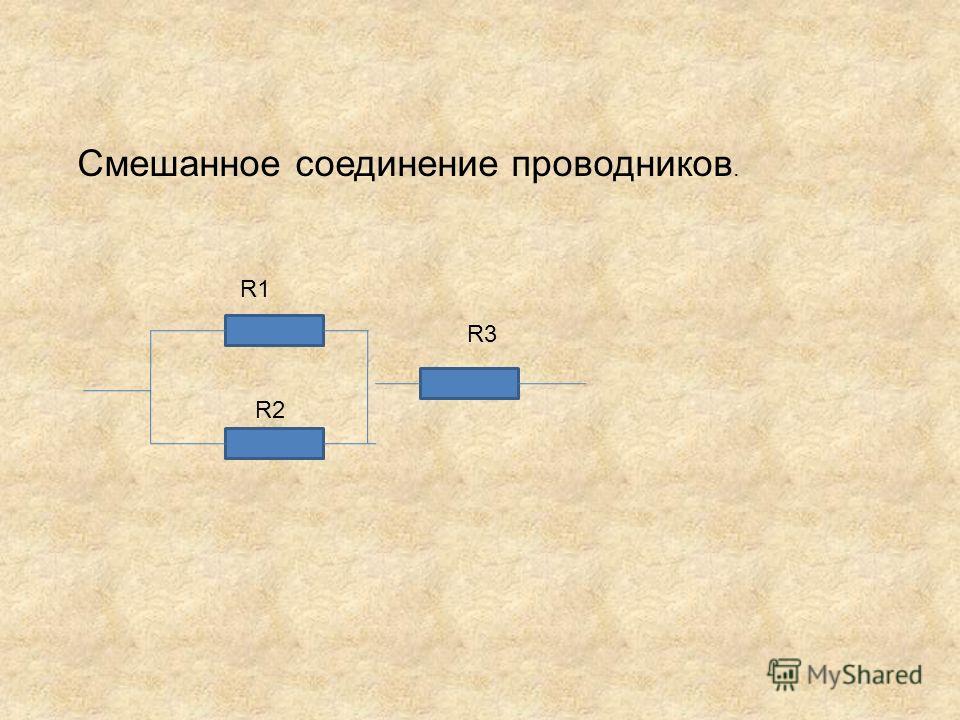
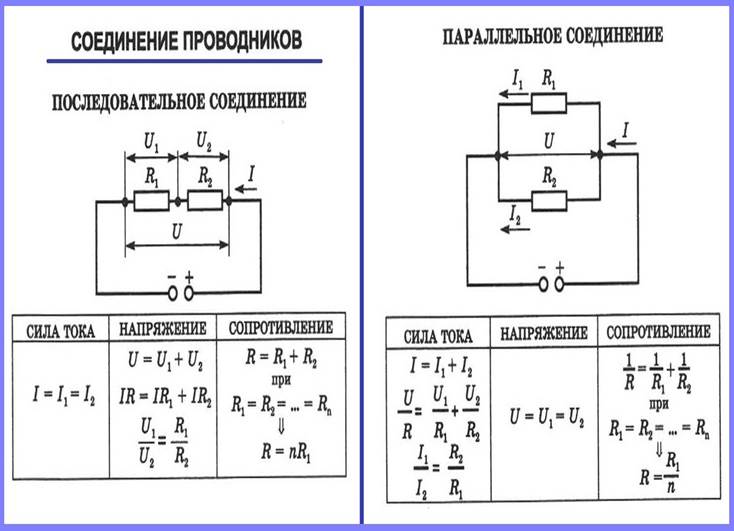


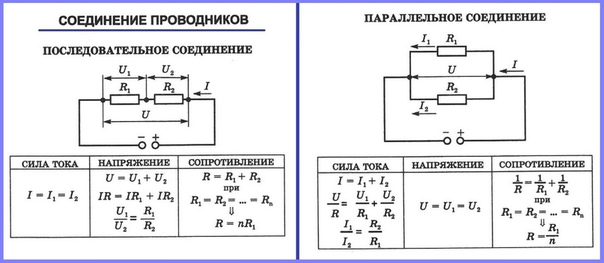 В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.