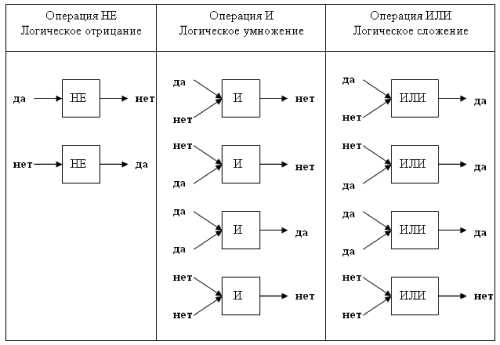
Оглавление. Таблицы истинности и логические операции

Кабинет информатики - Логические операции и таблицы истинности

Логические операции и таблицы истинности

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

F = A & B.

Логическое умножение  КОНЪЮНКЦИЯ  - это новое  сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.

 

 

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

F = A + B 

Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда  истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ

 

Логическое отрицание : ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным/ Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО

 

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

Логическое следование:  ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом  "следовательно"  и  выражается словами ЕСЛИ … , ТО …

 

 

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"

 

 

informatika11.ucoz.ru

Логические операции и таблицы истинности

Логические операции над высказываниями

1.     Отрицание.

Эта логическая операция соответствует в обыденной жизни частице «не».

Определение. Отрицанием высказывания x называется новое высказывание, которое является истинным, если высказывание  ложно, и ложным, если высказывание x истинно.

Отрицание высказывания x обозначается  и читается не x. Логические значения высказывания  модно описать с помощью таблицы, которая называется таблицей истинности:

x

1

0

0

1

Пусть x высказывание. Так как  тоже высказывание, то можно образовать отрицание высказывания , то есть высказывание , которое является двойным отрицанием высказывания x. Логические значения высказываний  и xсовпадают.

2.     Дизъюнкция (логическое сложение).

Эта логическая операция соответствует союзу «или».

Определение. Дизъюнкцией двух высказываний x, y называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний x или y истинно и ложным, если они оба ложны.

Дизъюнкция высказываний x, y обозначается xy и читается «x или y». Логические значения дизъюнкции описываются таблицей истинности:

x

y

xy

1

1

1

1

0

1

0

1

1

0

0

0

Высказывания x, y называются членами дизъюнкции.

Пример.

x – «5>3», y – «2>4». Тогда xy – «5>3»«2>4» истинно, так как истинно высказывание x.

В алгебре логики союз «или» всегда употребляется в неисключающем смысле. Из определения дизъюнкции и отрицания следует, что высказывание x всегда истинно.

3.     Конъюнкция.

Эта логическая операция соответствует союзу «и».

Определение. Конъюнкцией двух высказываний x, y называется новое высказывание, которое считается истинным, если оба высказывания x, y истинны, и ложным, если хотя бы одно из них ложно.

Конъюнкция высказываний x, y обозначается  и читается «x и y». Высказывания x, y называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности: 

x

y

1

1

1

1

0

0

0

1

0

0

0

0

Пример.

x – «6 делится на 2», y – «6 делится на 3». Тогда  – «6 делится на 2»«6 делится на 3» истинно.

Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания, далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.

Из определения операций конъюнкции и отрицания следует, что высказывание  всегда ложно.

4.     Импликация.

Эта логическая операция соответствует словам «если…,то…».

Определение. Импликацией двух высказываний x, y называется новое высказывание, которое считается ложным, если x истинно, а y ложно, и истинным во всех остальных случаях.

Импликация высказываний обозначается x→y и читается «если x, то y» или «из x следует y». Высказывание x называется условием или посылкой, а высказывание y – следствием или заключением. Высказывание x→y называется следованием или импликацией. Логические значения операции импликации описываются следующей таблицей истинности: 

x

y

x→y

1

1

1

1

0

0

0

1

1

0

0

1

Пример.

1)     x – «12 делится на 6», y – «12 делится на 3». Тогда импликация x→y – «если 12 делится на 6, то оно делится на 3» истинна, так как истинна посылка x, и истинно заключение y.

2)     x – «12 делится на 2 и 3», y – «12 делится на 7». Тогда импликация x→y – «если 12 делится на 2 и 3, то оно делится на 7» ложна, так как условие истинно, а заключение ложно.

Употребление слов «если…,то…» в алгебре логики отличается от употребления их в обыденной речи, когда, как правило, считается, что если высказывание x ложно, то высказывание «если x, то y» вообще не имеет смысла. Кроме того, строя предложение «если x, то y» в обыденной речи всегда подразумевается, что предложение y вытекает из предложения x. Употребление слов «если…, то…» в математической логике не требует этого, так как в ней смысл высказываний не рассматривается.

Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «если x, то y». Если при этом известно, что x истинно и доказана истинность импликации x→y то истинно и заключение y. В этом случае пишут xy и говорят, что из x следует y. Это классическое правило вывода постоянно используется в математике.

1.     Эквиваленция.

Эта логическая операция соответствует словам «тогда и только тогда, когда».

Определение. Эквиваленцией или эквивалентностью двух высказываний x, y называется новое высказывание, которое считается истинным, если оба высказывания x, y либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.

Эквиваленция высказываний x, y обозначается символом x↔y и читается «для того чтобы x, необходимо и достаточно, чтобы y» или «x тогда и только тогда, когда y». Логические значения операции эквиваленции описываютсяследующей таблицей истинности:

x

y

x↔y

1

1

1

1

0

0

0

1

0

0

0

1

Высказывания x, y называются членами эквиваленции.

Логические выражения и таблица истинности

 Таблица истинности - таблица, показывающая,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний.

Логическое выражение - составные высказывания в виде формулы.

Равносильные логическиевыражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения  таблицы  истинности:

1.    подсчитать количество переменных n в логическом выражении;

2.   определить число строк в таблице по формуле m=2n, где n - количество переменных;

3.   подсчитать количество логических операций в формуле;

4.   установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5.   определить количество столбцов: число переменных + число операций;

6.   выписать наборы входных переменных;

7.   провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.      разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.      разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.      продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

 

Пример 1. Для формулы  A/\ (B \/ ¬B /\¬C) постройте  таблицу истинности.

 Количество логических переменных 3, следовательно, количество строк - 23 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8.

 

 Пример 2. Определите истинность  логического выражения  F(А, В) = (А\/ В)/\(¬А\/¬В) .

1. В выражении две переменные А и В (n=2).

2.  mстрок=2n, m=22=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В;  2) ¬А;  3) ¬В;  4) ¬А\/¬В;  5) (А\/ В)/\(¬А\/¬В).

5. Кстолбцов=n+5=2+5=7 столбцов.

 

А

В

А\/ В

¬А

¬В

¬А\/¬В

F

0

0

0

1

1

1

0

0

1

1

1

0

1

1

1

0

1

0

1

1

1

1

1

1

0

0

0

0

 Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

 

Пример 3. Построёте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

1. В данной функции три логические переменные – А, В, С

2. количество строк таблицы = 23 =8

3. В формуле 3 логические операции.

4. Расставляем порядок действий

1) А\/ В;  2) ¬С; 3) (AVB) /\ ¬С  .

5. количество столбцов таблицы = 3 + 3 = 6

А

В

С

A\/B

¬С

(A\/B) /\ ¬С

0

0

0

0

1

0

0

0

1

0

0

0

0

1

0

1

1

1

0 font>

1

1

1

0

0

1

0

0

1

1

1

1

0

1

1

0

0

1

1

0

1

1

1

1

1

1

1

0

0

 

Пример 4.  Определите истинность формулы: F = ((С \/В)   В) /\ (А /\ В) => В.

Построим таблицу истинности этой формулы.

 

 

 Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

 

X

Y

Z

F

0

0

0

1

0

0

1

0

0

1

0

1

 

Какое выражение соответствует F?

 1) ¬X/\¬Y/\Z                      2) ¬X\/¬Y\/Z                  3) X\/Y\/¬Z              4) X\/Y\/Z

 Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X

Y

Z

F

¬X

¬Y

¬Z

¬X/\¬Y/\Z

¬X\/¬Y\/Z

X\/Y\/¬Z

X\/Y\/Z

0

0

0

1

1

1

1

0

1

1

0

0

0

1

0

1

1

0

1

1

0

1

0

1

0

1

1

0

1

0

1

1

1

 Очевидно, что значения заданной функции F совпадают со значениями выражения nt>X\/Y\/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

 Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y  и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

 Рассмотрим данный конкретный пример:

1)      первое заданное выражение  ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)      второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует  второй строке таблицы;

3)      третье выражение   X\/Y\/¬Z    соответствует F при всех предложенных комбинациях X,Y и Z;

4)      четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

Для самостоятельного выполнения

1. Построить таблицу истинности для выражения

   1. F= (AVB) & (¬AV¬B)

   2. XVY& ¬Z.

2. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y,Z. Дан фрагмент таблицы истинности выражения F:

X

Y

Z

F

0

0

0

1

0

0

1

0

0

1

0

1

Какое выражение соответствует F

1. ¬X /\ ¬Y /\ Z

2. ¬X V ¬Y V Z

3. X V Y V¬Z

4. X V Y V Z

3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y,Z. Дан фрагмент таблицы истинности выражения F:

X

Y

Z

F

1

0

0

1

0

0

0

1

1

1

1

0

Какое выражение соответствует F?

1. ¬X /\¬Y /\¬Z

2. X /\ Y /\ Z

3. X V Y V Z

4. ¬ X V¬Y V¬Z

referat-4all.ru

Основы логики. Логические операции и таблицы истинности

Логические операции и таблицы истинности

1) Логическое умножение или конъюнкция:

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.Обозначение: F = A & B; F = A и B; F = A and B; F = A /\ B

Таблица истинности для конъюнкции

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

 

2) Логическое сложение или дизъюнкция:

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.Обозначение: F = A + B; F = A или B; F = A or B; F = A V B

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

 

3) Логическое отрицание или инверсия:

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Таблица истинности для инверсии

 

4) Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

 

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;2. Конъюнкция;3. Дизъюнкция;4. Импликация;5. Эквивалентность.

Для изменения указанного порядка выполнения логических операций используются скобки.

Редактировалось Дата: Пятница, 05 Октябрь 2018

www.fordus.org.ua

---

• 
  Ветрогенератор промышленный
• 
  Что делать если документов на счетчики воды нет
• 
  Логическая схема это любая схема
• 
  Как крепить люстру на натяжной потолок
• 
  Санпин по освещенности рабочих мест
• 
  Схема подключения тт к счетчику
• 
  Законы кирхгофа примеры
• 
  Диаметр от сечения провода
• 
  Передача электроэнергии по воздуху
• 
  Правила замены электросчетчика в многоквартирном доме
• 
  Выпрямитель в схеме