Магнитная цепь | Проектирование электрических машин переменного тока
Страница 5 из 40
ГЛАВА ТРЕТЬЯ
МАГНИТНАЯ ЦЕПЬ
1. ОБЩИЕ ПОЛОЖЕНИЯ
Магнитная цепь машины переменного тока образуется за счет сердечников статора и ротора. Воздушный зазор, расположенный между этими двумя частями, играет большую роль в определении параметров и технико-экономических показателей машины.
В связи с тем, что обмотки обтекаются токами, в активных и частично конструктивных элементах машины возбуждаются магнитные поля. С точки зрения упрощения физической картины и электромагнитного расчета разделяют магнитные поля в машине на основное поле и поля рассеяния.
Основное магнитное поле создается с целью индуктирования в рабочей обмотке необходимой э. д. с. Поля рассеяния сопутствуют протеканию по обмоткам токов.
Магнитная цепь предназначается для создания пути основного потока. С этой целью сердечники ротора и статора выполняются из хорошо проводящих магнитных материалов.
Поля рассеяния в электрических машинах в основном проходят по воздуху, однако в какой-то мере они замыкаются и через сердечники и таким образом частично нагружают их.
Основной магнитный поток всегда вращается относительно якоря и, следовательно, относительно его сердечника. Относительно индуктора основной поток в синхронных машинах неподвижен, а в асинхронной машине вращается относительно ротора со скоростью скольжения.
В соответствии с этим должны предъявляться требования к конструкции сердечников якоря и индуктора. Сердечник якоря должен выполняться из шихтованной электротехнической стали с изолированными друг от друга листами. Индуктор может быть выполнен из обычной конструктивной или листовой малолегированной стали.
Основное поле машины под нагрузкой возбуждается за счет взаимодействия токов во всех обмотках. Построение поля под нагрузкой является довольно сложной задачей. Поэтому в практике проектирования и расчета очень часто рассматривают поля в режиме холостого хода при номинальном напряжении и в режиме установившегося короткого замыкания при номинальном токе якоря.
Рис. 3-1. Петля гистерезиса (а) и кривая намагничивания роторной стали (б)
Результирующее поле не может быть, строго говоря, найдено наложением двух этих режимов из-за нелинейной связи между индукцией и напряженностью магнитного поля в ферромагнитных сердечниках. Тем не менее, многие практические методы расчета с успехом базируются на приближенных методах наложения.
Проектирование и расчет магнитной цепи связан с построением или определением магнитных полей и определением интенсивности их на отдельных участках магнитопровода.
Основной зависимостью, связывающей магнитную индукцию и напряженность магнитного поля Н, является следующая: μ = Β/Η, где μ — магнитная проницаемость среды.
Магнитная проницаемость ферромагнитных материалов обычно записывается в виде: μ = μ0μе, где μ0—магнитная проницаемость пустоты, μe — относительная магнитная проницаемость.
Если индукция В выражается в тл, а напряженность магнитного поля в а/м, то магнитная проницаемость пустоты будет μ0 = 0,4 π·10-6 гн/м. Часто на практике II выражают в а/см, а В в тл, тогда μ0 = 0,4π·10-8 гн/см.
Для сталей зависимость В = / (Я) носит нелинейный характер. При циклическом перемагничивании стали имеет место так называемая петля гистерезиса (рис. 3-1, а). Основная кривая намагничивания образуется соединением вершин отдельных петель. Остаточная индукция, которая имеет место при Н = 0, обеспечивает в машинах остаточное напряжение при вращении синхронных машин без возбуждения. Остаточное напряжение в машинах обычно мало, но им можно воспользоваться при определении, например, симметрии э. д. с. в фазах. Коэрцитивная сила Нэ соответствует нулевому значению индукции В.
Типичная кривая намагничивания роторной стали показана на рис. 3-1, б. При больших значениях Н имеет место насыщение. При расчетах магнитной цепи пользуются либо графическим, либо табличным методом написания зависимости В — f (Н).
При приближенных расчетах, а также при аналитических исследованиях прибегают к замене действительной кривой намагничивания ломаном линией, причем в зоне до колена насыщения с успехом может быть введена приближенная зависимость вида В = аН, где а — постоянная, определяемая сортом стали.
В зоне сильного насыщения уравнение прямой можно записать в виде
где Ва обычно может составить 2—2,2 тл в зависимости от сорта стали.
Рис. 3-2. Зависимость магнитной проницаемости роторной стали от напряженности поля
Зависимость магнитной проницаемости стали от напряженности поля показана на рис. 3-2. При малых значениях напряженности магнитная проницаемость имеет тенденцию к росту вместе с ростом Н. После достижения своего максимального значения рm магнитная проницаемость падает по мере роста напряженности магнитного поля.
Зона, где μ возрастает при увеличении интенсивности магнитного поля, называют зоной слабых магнитных полей. В зоне сильных магнитных полей по мере роста Н или В магнитная проницаемость падает.
Обычно в номинальных или близких к ним режимах в магнитопроводе имеют место сильные поля. Однако сложный характер μ делает несколько неопределенными значения некоторых параметров в ненасыщенном состоянии.
Теоретически ненасыщенное состояние определяется при условии μ=∞. Для стали μ, может быть больше единицы в десятки и тысячи раз.
При определении основных характеристик и параметров машины основную долю магнитного сопротивления составляют воздушные промежутки, или воздушные зазоры.
При магнитных потоках значительно ниже номинального магнитное сопротивление стали становится настолько малым, что отдельные характеристики определяются полностью воздушными промежутками, т. е. становятся линейными. Однако при чрезвычайно слабых магнитных полях магнитное сопротивление стали начнет возрастать.
Каждый линейный интеграл будет определяться как магнитное падение напряжения на данном участке.
Магнитную цепь для основного потока электрических машин переменного тока обычно принято разбивать на следующие участки (рис. 3-4): воздушный зазор, зубцовая зона статора, ярмо сердечника статора, полюсная, или зубцовая, зона ротора, ярмо ротора. Магнитный расчет обычно производят на два полюса или на один полюс.
Условия нахождения магнитных падений напряжения на различных участках магнитопровода рассмотрены в § 3-2, 3-3 и 3-4.
Применительно к потокам рассеяния линейные интегралы ∫ Н dl выбираются в зависимости от конкретных условий.
Рис. 3-4. Магнитная цепь двухполюсного турбогенератора
1— воздушный зазор, 2 — зубцовая зона статора, 3 — ярмо сердечника статора, 4 — зубцовая зона ротора, 5— ярмо ротора
Сумма, стоящая в левой части уравнения (3-2), представляет собой полный ток, охватываемый контуром интегрирования. Эта сумма представляет собой сумму н. с. F, развиваемых всеми обмотками, которые охвачены контуром интегрирования.
Рис. 3-3. Зависимость сверхпереходного индуктивного сопротивления от линейной нагрузки, снятая при питании обмотки статора пониженным током
Поскольку распределение н. с. в пространстве и во времени может быть достаточно сложным, основную характеристику намагничивания определяют обычно с учетом обтекания током только обмотки намагничивания (обмотки возбуждения для синхронных машин и обмотки якоря для асинхронных). В простейшем случае, если токи во всех витках одинаковые и число витков равно W, то полный ток определится как
(3-3)
При расчете магнитной характеристики машины удобно считать, что величина основного потока холостого хода Ф0 задана и необходимо определить магнитные падения напряжения на отдельных участках цепи и полную н. с., необходимую для проведения этого потока через всю цепь.
При расчете потоков рассеяния исходят из заданных значений токов в обмотках.
Для определения линейных интегралов от напряженности магнитного поля необходимо знать распределение магнитного поля на данном участке. Следовательно, для расчета магнитной цепи с той или иной степенью приближения должна быть найдена картина поля на различных участках магнитопровода.
При определении магнитных полей в электрических машинах обычно
делаются следующие допущения:
- В основном рассматриваются двухмерные, плоские задачи: в поперечном сечении машины для основного потока и пазового рассеяния, в продольном сечении для рассеяния в лобовых и торцевых частях.

- Все области, запятые магнитным потоком, являются безвихревыми, т. е. свободными от токов. Поэтому все обтекаемые током обмотки заменяются либо точечным, либо линейным распределением токов. При переменных магнитных полях в сердечниках эффект вытеснения потока в них должен практически отсутствовать.
- Картина поля в воздушном зазоре и воздушных промежутках строится при условии, что магнитная проницаемость μ всех стальных деталей на границе с рассматриваемой областью равна бесконечности.
- Поле в ферромагнитных телах в простейших случаях может определяться при μе=const, а затем вносятся поправки на нелинейность μе.
- Потоки рассеяния обычно не зависят от насыщения, поскольку они в основном проходят по воздуху.
Магнитный поток, проходящий через различные участки цепи, подчиняется следующим законам прохождения на границе сред:
Рис. 3-5. Картина поля синхронной явнополюсной машины при холостом ходе: Сплошными проведены силовые линии, штриховыми — линии магнитного потенциала.
нормальные составляющие индукции на границе раздела равны, Вni = Bn2; нормальные составляющие напряжённости магнитного поля относятся как Hη1/Hη2 = μe2/μe1;касательные составляющие напряженности на границе раздела равны, Ht1= Ht2;касательные составляющие индукции относятся как Bt1IBt2=μе1/μе2.
Если осуществляется переход из стали в воздух, то и, поскольку μe > 1, то почти всегда можно считать, что линии магнитного поля перпендикулярны к поверхности стали.
В том случае, если на границе сред имеет место линейная токовая нагрузка А, на поверхности раздела будем иметь для напряженности магнитного поля Нt1 = Нt2 ± A, а для касательных составляющих индукции
Следовательно, при наличии линейной нагрузки на границе воздуха и стали линии магнитного потока не будут строго перпендикулярны к поверхности стали, а будут иметь тем большую тангенциальную составляющую, чем больше величина линейной нагрузки A. Это обстоятельство следует учитывать при построении картины поля при наличии линейной нагрузки на разделе стали и воздуха, например в воздушном зазоре или на сердечнике полюса.
Для магнитной цепи может быть введено магнитное сопротивление R и магнитная проводимость λ, которые связаны соотношением: λ = 1 /R.
Магнитная проводимость определяется из (3-2), если правую часть умножить на λ, а левую на μ: λ = Ф/F, где F — н. с., необходимая для проведения потока Ф на рассматриваемом участке.
Основные уравнения электромагнитного поля, учитывая безвихревой характер ноля, будут
Для плоской задачи в прямоугольных координатах будем иметь:
(3-4)
(3-5)
Магнитная цепь машины постоянного тока
Если по катушкам машины постоянного тока, расположенным на главных полюсах, начнет протекать ток, вокруг катушек полюсов будет создаваться магнитное поле.
В зависимости от направления тока в обмотке возбуждения, полюса будут иметь разную полярность.
Для того чтобы машина постоянного тока могла работать, число полюсов всегда должно быть парным.
Магнитное поле обозначается магнитными силовыми линиями. Направление всегда от северного полюса к южному.
Магнитные силовые линии в машине постоянного тока должны быть замкнуты между полюсами противоположной полярности.
При расчете магнитной цепи принято использовать среднюю магнитную силовую линию. Прежде чем нарисовать эту линию, введем понятие средней линии полюсов.
Средняя линия полюсов — это плоскость, проходящая вдоль машины через центр посередине полюсов. Средняя магнитная силовая линия обозначает основной магнитный поток, который обозначается Фδ.
Основным магнитным потоком называется поток, создаваемый полюсом и через воздушный зазор сцепляющийся с обмоткой якоря. Число основных магнитных потоков равно числу полюсов.
Eа=Cм·Фδ·ω
M=Cм·Фδ·Iа
Pэм=Eа·Iа
Eа — ЭДС обмотки якоря.
Cм — машинная постоянная. Она зависит от конструкции якоря машины и для каждой конкретной машины — величина постоянная.
Она зависит от конструкции якоря машины и для каждой конкретной машины — величина постоянная.
Фδ — основной магнитный поток.
ω — угловая скорость вращения.
M — момент, развиваемый двигателем на валу.
Iа — ток якоря.
Pэм — электромагнитная мощность. Служит доказательством того, что от магнитного потока зависит мощность машин.
Кроме основного магнитного потока вокруг полюсов создаются магнитные потоки, которые не соединяются с якорем, они называются потоками рассеяния и обозначаются Фσ. Потоки рассеяния возникают в местах крепления железа полюса к корпусу и на концах башмаков.
Основной задачей расчета магнитной цепи является определение числа витков и тока одного витка, необходимых для создания магнитного потока и проведения его через магнитную цепь машины.
Произведение числа витков на ток называется намагничивающей силой цепи. Величина намагничивающей силы цепи зависит от сопротивления цепи прохождению магнитного потока.
Для того чтобы определить сопротивление магнитной цепи, ее делят на участки, исходя из условия, что магнитное сопротивление, выражаемое в напряженности по всей длине участка, будет постоянным. Таких условий пять:
1. Воздушный зазор и его магнитное сопротивление.
Fδ=Hδ·δ
Hδ — напряженность воздушного зазора.
2. Зубцы якоря.
Fz=Hz·hz
Fz — магнитное сопротивление зубца;
Hz — напряженность в зубце;
hz — высота зубца.
3. Ярмо якоря.
Fа=Hа·Lа
Fа — магнитное сопротивление ярма;
Hа — напряженность в ярме;
Lа — длина магнитной силовой линии.
4. Полюса.
Fm=Hm·hm
hm — длина магнитной силовой линии (высота статора).
5. Магнитное сопротивление ярма статора.
Fя=Hя·Lя
Lя — длина магнитной силовой линии в ярме статора.
Намагничивающая сила цепи должна быть равна сумме магнитных сопротивлений участков цепи.
Fц=Fδ+Fz+Fа+Fm+Fя=100%
Fц=wв·iв
Воздушный зазор в машине постоянного тока колеблется от 2 до 4 мм и, несмотря на такую маленькую величину, воздушный зазор оказывает самое большое сопротивление прохождению магнитного потока.
От точности расчета воздушного зазора зависит точность определения намагничивающей силы цепи, а соответственно мощности и габаритов машины.
Магнитная цепь
Пользователи также искали:
из каких элементов состоит простейшая магнитная цепь,
какие бывают магнитные цепи,
магнитная цепь классификация,
магнитная цепь пример,
магнитные цепи лекция,
неразветвленная магнитная цепь,
однородная магнитная цепь,
разветвленная магнитная цепь,
Магнитная,
магнитная,
цепь,
Магнитная цепь,
цепи,
магнитные,
однородная магнитная цепь,
магнитная цепь классификация,
неразветвленная магнитная цепь,
магнитные цепи лекция,
пример,
разветвленная,
однородная,
классификация,
какие,
бывают,
неразветвленная,
каких,
элементов,
состоит,
простейшая,
лекция,
разветвленная магнитная цепь,
магнитная цепь пример,
какие бывают магнитные цепи,
из каких элементов состоит простейшая магнитная цепь,
магнитная цепь,
электромагнетизм. магнитная цепь,
магнитная цепь,
…
Для чего нужен расчет магнитной цепи?
Расчет магнитных цепей
Задачей расчета почти всегда является определение намагничивающей силыIwнужной для того, чтоб возбудить в магнитопроводе определенный магнитный поток либо определенную магнитную индукцию в неком участке магнитной цепи (в большинстве случаев в воздушном промежутке).
Расчет ведется на основании закона полного тока, согласно которому сумма магнитных напряжений на отдельных участках магнитной цепи равна намагничивающей силе:
Н1lл+ h2l1+ … + Hklk+ … + Hnln= ? Hklk= Iw, при (k=n, k=1)
тут магнитным напряжением именуется произведение напряженности поля Нkна длину соответственного участка, т. е. Hklk.
Магнитная цепь делится по способности на маленькое число nучастков, в границах каждого из которых можно принять напряженность Hи индукцию Внеизменными (на рис.1 п =3). Потом, если задан магнитный поток Ф, то для 1-го из участков, имеющего сечение S1, определяется магнитная индукция B1= ф :S1
Рис.1 Магнитная цепь с магнитным зазорома на основании значения магнитной индукции В1при помощи кривой намагничивания ферромагнитного материала этого участка сердечника определяется напряженность h2соответственнаяиндукцииВ1(рис.2). В таком же порядке для второго участка необходимо отыскать поначалу В2=Ф:S2, а потом по кривой намагничивания h3.
Таким методом поочередно определяется значение напряженности для всех nучастков магнитной цепи.Если в магнитной цепи имеется воздушный просвет (либо неферромагнитный участок), то сечение пути потока в воздухе можно принять равным сечению прилегающего ферромагнитного участка. Как следует, индукция в воздушном промежутке Ввравна индукции на этом примыкающем участке. На основании этой индукции определяем напряженность магнитного поля; обычно в воздухе она оказывается достаточно большой: Hв= Bв:µ0
Рис. 2 Определение напряженности поля при помощи кривой намагничиванияиз-за того что магнитная проницаемость воздуха µвоз=µ0относительно мала и потому для возбуждения сколько-либо значительной индукции нужна большая напряженность поля.Длиной каждого из участков магнитной цепи следует считать длину пути потока, т.
2 Определение напряженности поля при помощи кривой намагничиванияиз-за того что магнитная проницаемость воздуха µвоз=µ0относительно мала и потому для возбуждения сколько-либо значительной индукции нужна большая напряженность поля.Длиной каждого из участков магнитной цепи следует считать длину пути потока, т.
е. длину средней магнитной полосы.После того как определено магнитное напряжение Hlдля всех участков цепи, пользуясь законом полного тока, подсчитываем нужную намагничивающую силу: h2l1+ h3l2+…+ Hвlв=Iwлибо, если понятно число витков катушки, то I=( h2l1+ h3l2+…+ Hвlв):wПри расчете полезно направить внимание на то, что на маленький воздушный просвет затрачивается большая часть намагничивающей силы.Если же необходимо решить оборотную задачку, найти магнитный поток либо индукцию по данной намагничивающей силе Iw, то расчет несколько усложняется из-за того, что непонятно рассредотачивание напряженности Н меж отдельными участками магнитной цепи, а оно находится в зависимости от неведомой магнитной индукции. По этой причине задачку приходится решать методом подбора либо средством построения магнитной свойства устройства.Необходимо задаться неким возможным значением магнитного потока Ф’(либо индукции для 1-го из участков) и рассчитать, как это было изготовлено выше, намагничивающую силу Iw’, нужную для возбуждения этого потока.
Приобретенное таким методом значение Iw’следует сравнить с данным значением Iw. Если Iw’значительно отличается от Iw, то необходимо повторить расчет, задавшись новым значением потока Ф”;на основании этого расчета отыскать новое значение Iw”и т. д.Кривая зависимости потока Фот намагничивающей силы I w, построенная средством таких расчетов, выполненных примерно для 5 значений Ф, будет представлять собой магнитную характеристику цепи. С помощью таковой характеристики просто найти поток, соответственный хоть какому значению намагничивающей силы.Ц.ель работы: Изучение параметров магнитной цепи, методики расчета неразветвленной магнитной цепи.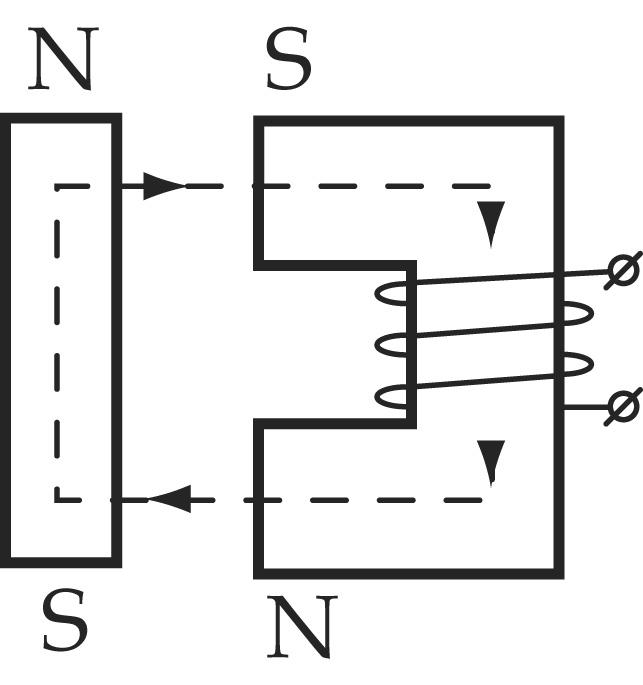 Студент должен:Знать- основные параметры магнитной цепи, их взаимосвязь, единицы измерения.Уметь – выполнять расчеты неразветвленной магнитной цепи (прямая и обратная задача).Показать навыки— работы с таблицами, графиками; навыки аналитических расчетов.
Студент должен:Знать- основные параметры магнитной цепи, их взаимосвязь, единицы измерения.Уметь – выполнять расчеты неразветвленной магнитной цепи (прямая и обратная задача).Показать навыки— работы с таблицами, графиками; навыки аналитических расчетов.
Магнитная цепь и ее расчет
Магнитная цепь (МЦ) — это устройство из ферромагнитных сердечников с воздушными зазорами или без них, по которым замыкается магнитный поток. Применение ферромагнетиков имеет целью получение наименьшего магнитного сопротивления, при котором требуется наименьшая МДС для получения нужной магнитной индукции или магнитного потока.
Простейшая магнитная цепь — это сердечник кольцевой катушки. Применяются магнитные цепи неразветвленные и разветвленные, отдельные участки которых выполняются из одного или из разных материалов. Расчет магнитной цепи сводится к определению МДС по заданному магнитному потоку, размерам цепи и ее материалам.
Для расчета цепь делят на участки l1,l2и т. д. с одинаковым сечением по всей длине участка, т.
е. с однородным полем, определяют магнитную индукцию В=на каждом из них и по кривым намагничивания находят соответствующие напряженности магнитного поля. Магнитная цепь (MЦ)состоит из двух основных элементов: – источника магнитной энергии; – магнитопровода.
Источник магнитной энергии в реальных МЦ бывает двух видов:
– постоянный магнит; – электромагнит.
Электромагнит представляет собой катушку индуктивности, размещенную на магнитопроводе, и подключенную к источнику напряжения.
Магнитопровод по своей конструкции может быть разветвленным и неразветвленным.
На рис.1. полказана неразветвленная магнитная цепь с электромагнитом.
Основные параметры МЦ:
- МДС – магнитодвижущая сила (основной параметр источника магнитной энергии):
F= Iw(A), где I- ток в обмотке (А), w- число витков обмотки электромагнита.
- Напряженность магнитного поля на любом участке МЦ.
Н = = w,(). lср–длина средней линии магнитопровода (м). lсрпроводится на чертеже строго по середине сечения магнитопровода.
3.магнитная индукция: В = µ µ0Н (Тл), где µ – магнитная проницаемость вещества, из которого изготовлен магнитопровод.
µ0 – магнитная постоянная, µ0= 4 π ∙10 -7Гн /м
4.Магнитный поток: Ф = В ∙S(Вб), где S- площадь поперечного сечения магнитопровода.
4. Задача на расчет магнитной цепи Задача 1. Прямая задача расчета мц
По заданному магнитному потоку в цепи необходимо определить намагничивающую силу (МДС), необходимую для создания этого потока. Решение задачи варианта №32.
варА,ммВ,мма,ммb,ммс,ммd,ммδ,ммПрямая задачаОбратная задачаВδ,ТлI,АматериалI,Аw,витматериал322903307040603040,50,1чугун0,21300чугун333002506050403091,90,5Электротех.сталь0,41900литая сталь
Определить число витков wкатушки электромагнита, если известны габариты магнитопровода, индукция Вδв воздушном зазоре, материал магнитопровода и ток Iв обмотке электромагнита Толщина провода магнитопровода по всей длине одинакова и составляет 100 мм.
Задачей расчета в большинстве случаев является определение намагничивающей силы Iw, необходимой для того, чтобы возбудить в магнитопроводе определенный магнитный поток или определенную магнитную индукцию в некотором участке магнитной цепи (чаще всего в воздушном промежутке).Схема расчета магнитных цепей.Расчет ведется на основании закона полного тока, согласно которому сумма магнитных напряжений на отдельных участках магнитной цепи равна намагничивающей силе:Н1lл+ h2l1+ … + Hklk+…
+ Hnln= ? Hklk= Iw, при (k=n, k=1)Здесь магнитным напряжением называется произведение напряженности поля Нkна длину соответствующего участка, т. е.
Hklk.Магнитная цепь делится по возможности на небольшое число n участков, в пределах каждого из которых можно принять напряженность H и индукцию В постоянными (на рис. 1 п = 3). Затем, если задан магнитный поток Ф, для одного из участков, имеющего сечение S1, определяется магнитная индукция B1= ф :S1Рисунок 1. Схема магнитной цепи с магнитным зазором.А на основании значения магнитной индукции В1с помощью кривой намагничивания ферромагнитного материала этого участка сердечника определяется напряженность h2соответствующая индукции В1(рис.2).
1 п = 3). Затем, если задан магнитный поток Ф, для одного из участков, имеющего сечение S1, определяется магнитная индукция B1= ф :S1Рисунок 1. Схема магнитной цепи с магнитным зазором.А на основании значения магнитной индукции В1с помощью кривой намагничивания ферромагнитного материала этого участка сердечника определяется напряженность h2соответствующая индукции В1(рис.2).
В таком же порядке для второго участка нужно найти сначала В2=Ф:S2, а затем по кривой намагничивания h3. Таким путем последовательно определяется значение напряженности для всех n участков магнитной цепи.Если в магнитной цепи имеется воздушный промежуток (или неферромагнитный участок), то сечение пути потока в воздухе можно принять равным сечению прилегающего ферромагнитного участка. Следовательно, индукция в воздушном промежутке Ввравна индукции на этом соседнем участке.
На основании этой индукции определяем напряженность магнитного поля. Обычно в воздухе она оказывается довольно большой: Hв= Bв:µ 0,Из-за того что магнитная проницаемость воздуха µвоз=µ0относительно мала, и поэтому для возбуждения сколько-нибудь значительной индукции нужна большая напряженность поля.Длиной каждого из участков магнитной цепи следует считать длину пути потока, т. е.
длину средней магнитной линии.После того как определено магнитное напряжение Hl для всех участков цепи, пользуясь законом полного тока, подсчитываем необходимую намагничивающую силу: h2l1+ h3l2+…+ Hвlв=IwИли, если известно число витков катушки, то I=( h2l1+ h3l2+…+ Hвlв):wПри расчете полезно обратить внимание на то, что на маленький воздушный промежуток затрачивается большая часть намагничивающей силы.Рисунок 2. График определения напряженности поля.Если же нужно решить обратную задачу, определить магнитный поток или индукцию по заданной намагничивающей силе Iw, то расчет несколько усложняется из-за того, что неизвестно распределение напряженности Н между отдельными участками магнитной цепи, а оно зависит от неизвестной магнитной индукции. По этой причине задачу приходится решать путем подбора или посредством построения магнитной характеристики устройства.
По этой причине задачу приходится решать путем подбора или посредством построения магнитной характеристики устройства.
Нужно задаться некоторым вероятным значением магнитного потока Ф’ (или индукции для одного из участков) и рассчитать, как это было сделано выше, намагничивающую силу Iw’, необходимую для возбуждения этого потока. Полученное таким путем значение Iw’ следует сопоставить с заданным значением Iw. Если Iw’ существенно отличается от Iw, то нужно повторить расчет, задавшись новым значением потока Ф”; на основании этого расчета найти новое значение Iw” и т. д.http://fazaa.ru/www.youtube.com/watch?v=E1haHQA1MOgКривая зависимости потока Ф от намагничивающей силы I w, построенная посредством таких расчетов, выполненных примерно для пяти значений Ф, будет представлять собой магнитную характеристику цепи.При помощи такой характеристики легко определить поток, соответствующий любому значению намагничивающей силы.Поделитесь полезной статьей:
Магнитной цепью или магнитопроводом называется путь, по которому замыкается магнитный поток. Этот путь может проходить целиком по воздуху.
Рисунок 1. Примеры магнитных цепей
На рисунке 1, апоказан соленоид. Магнитная цепь здесь проходит через воздух. Магнитное сопротивление воздуха очень велико, поэтому даже при большой намагничивающей силе магнитный поток мал.
Для увеличения магнитного потока в состав магнитной цепи вводят ферромагнитные материалы (обычно литая или электротехническая сталь), имеющие меньшее магнитное сопротивление.
На рисунке 1, бпредставлен прямой электромагнитс разомкнутым сердечником. Магнитные линии только небольшую часть своего пути проходят по стальному сердечнику, большую же часть своего пути они проходят по воздуху. Полюсы электромагнита определяются при помощи “правила буравчика”.
Подковообразный электромагнит, изображенный на рисунке 1, в, представляет магнитную цепь с лучшими условиями для прохождения магнитного потока. При такой конструкции поток большую часть пути проходит по стали и меньшую часть от полюса Nдо полюса Sпо воздуху.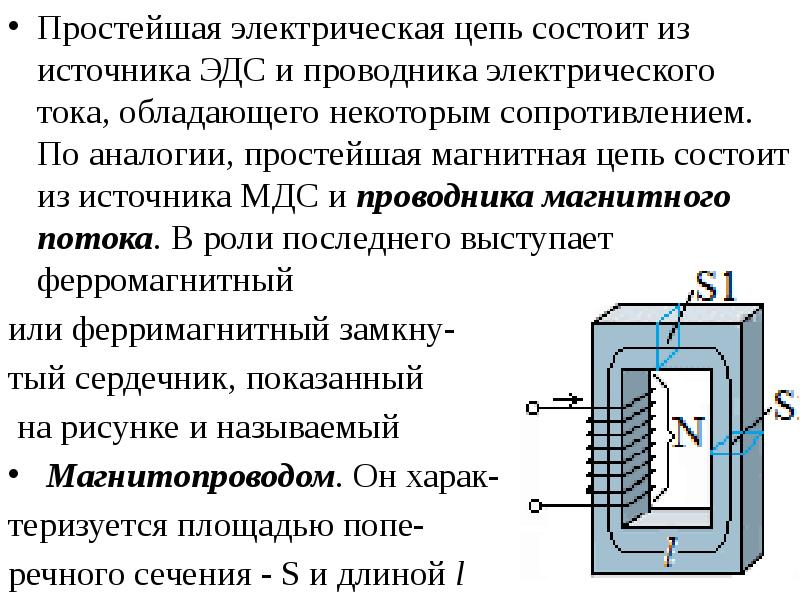
На рисунке 1, гпредставлена конструкция магнитной цепи, применяемая в электромашиностроении и приборостроении. Между полюсами электромагнита помещается стальной якорь. Большую часть своего пути магнитные линии проходят по стали и только очень малую часть (от нескольких долей миллиметра до 2–3 мм) проходят по двум воздушным промежуткам.
Трансформаторы имеют замкнутый стальной сердечник (рисунок 1, д). Сердечники трансформаторов собираются из нескольких частей, но во время сборки принимают меры к тому, чтобы воздушные зазоры между отдельными частями практически были равны нулю.
До сих пор мы не говорили о том, что магнитный поток, созданный намагничивающей силой, не весь замыкается по тому пути, который ему предназначен. Помимо рабочего магнитного потока, существует магнитный поток рассеяния, который замыкается вне того места, где используется рабочий поток. На рисунке 1, б, в, г, дпоказаны потоки рассеяния.
Таким образом, общий магнитный поток, который должна создать обмотка возбуждения электромагнита, равен сумме рабочего потока и потока рассеяния.
Расчет магнитной цепи, казалось бы, можно производить по формуле:
Но если вспомнить, что относительная магнитная проницаемость µ для ферромагнитных тел непостоянна и зависит от многих причин, то становится ясно, что этой формулой можно пользоваться лишь в том случае, когда в состав магнитной цепи входят только немагнитные тела (в том числе и воздух), для которых µ есть заранее заданная величина.
На практике для расчета магнитных цепей предпочитают пользоваться графическими методами решения.
Расчет магнитной цепи производят в следующем порядке. Задаются необходимой величиной магнитного потока. Разбивают магнитную цепь на участки, имеющие одинаковые поперечные сечения и однородный материал, и для каждого участка определяют величину магнитной индукциипо формуле:
Затем по кривым намагничиваниядля данного материала находят для каждого значения магнитной индукции величину напряженности H. Если в магнитной цепи встречаются воздушные зазоры, то зависимость B0и H0определяется по формуле:
Здесь B0выражено в Вб/м², µ0– в Гн/м, H0– в А/см .
Если индукция выражена в гауссах, а напряженность в А/см, то зависимость между B0и H0будет:
H0= 0,8 × B0.
Определив величину Hдля каждого участка, находим по закону полного токавеличину намагничивающей силы по формуле:
Пример.Найти намагничивающую силу обмотки электромагнита, изображенного на рисунке 2.
Размеры даны в миллиметрах.Материал сердечника – электротехническая сталь. В сердечнике необходимо создать магнитный поток 60 000 Мкс. Магнитным рассеянием пренебрегаем.
Рисунок 2. К примеру расчета магнитной цепи
Проводим среднюю линию по все длине магнитной цепи. Разбиваем цепь на пять участков и определяем длину каждого участка.
Так как магнитный поток во всех участках одинаков и площадь поперечного сечения всех участков магнитной цепи (2 × 2 см), то магнитная индукция везде также будет одинакова.
По кривой намагничивания (рисунок 3) для электротехнической стали по индукции 15000 Гс находим напряженность магнитного поляH= 30 А/см. Для воздушного зазора имеем:
H0= 0,8 × 15000 = 12000 А/см .
Рисунок 3.
Кривые намагничивания электротехнической стали, литой стали и чугунаУмножая величины напряженности на длины соответствующих участков, получаем произведения H× lдля этих участков.Результаты вычислений записываем в таблицу (таблица 1).Таблица 1Номера участковМатериалBlHH× lГссмА/смАI II и VI III и VIV Электротехническая сталь То же То жеВоздух15000 15000 15000150008 10 × 2 3,8 × 20,430 30 3012000240 600 2284800I× w= ∑ (H× l) = 5868 А .Интересно отметить, что если на участках из электротехнической стали I, II, III, V и VI общей протяженностью 35,6 см (8 + 20 + 7,6 см) для проведения магнитного потока необходима намагничивающая сила 1068 А (240 + 600 + 228 А), то на воздушный зазор длиной всего 4 мм (в 89 раз меньше длины пути стали) нужна намагничивающая сила 4800 А. Отсюда становится понятной необходимость создания магнитных цепей с минимальными воздушными зазорами.Источник:Кузнецов М. И., “Основы электротехники” – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.
Источники:
- elektrica.info
- studfiles.net
- fazaa.ru
- www.electromechanics.ru
Неоднородная магнитная цепь — Большая Энциклопедия Нефти и Газа, статья, страница 1
Неоднородная магнитная цепь
Cтраница 1
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых кроме участков из ферромагнитных материалов имеются воздушные зазоры.
[2]
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых, кроме участков из ферромагнитных материалов, имеются воздушные зазоры.
[4]
Неоднородную магнитную цепь ( рис. 3 — 11) можно рассматривать как состоящую из двух ( для данной задачи) последовательно соединенных участков магнитных сопротивлений.
[6]
Неоднородной магнитной цепью называется цепь, состоящая из участков различного сечения и из различных материалов, в том числе и воздушных зазоров.
[8]
Если применить к рассмотренным выше однородным и неоднородным магнитным цепям закон полного тока, то можно получить соотношения, необходимые для расчета магнитных цепей.
[9]
Порядок решения прямой задачи для неоднородной магнитной цепи следующий. Вся цепь разбивается на отдельные участки, отличающиеся друг от друга неоднородностью материала или различным сечением магнитопровода.
[10]
Для вывода этого закона рассмотрим неоднородную магнитную цепь, изображенную на рис. 3.8. Здесь магнитная цепь неоднородна по материалу ( содержит воздушный зазор) и по сечению. Следовательно, напряженность магнитного поля в пределах каждого участка — величина постоянная.
[11]
В чем состоит графо-аналитический метод расчета неоднородной магнитной цепи при решении обратной задачи.
[12]
Это уравнение применяют для решения прямой задачи расчета неоднородной магнитной цепи. Неразветвленную цепь в этом случае делят на однородные участки и для каждого из них определяют магнитную индукцию В, а затем находят значения напряженности магнитного поля Нп и магнитного напряжения Umn. По уравнению (3.23) определяют намагничивающую силу F, необходимую для получения заданного магнитного потока.
[13]
Из полученного выражения составим формулу закона магнитной цепи для неоднородной магнитной цепи.
[14]
Страницы:
1
2
Классификация, элементы и характеристики магнитных цепей
Для электрических машин и многих электротехнических устройств основным функциональным элементом является магнитная система. Обычно магнитную систему представляют в виде магнитной цепи.
Магнитная цепь содержит источники магнитного поля, систему магнитопроводов из ферромагнитного материала, другие вещества или воздушный зазор, по которым замыкается магнитный поток (рис. 25.1).
Рис.26.1. Неразветвленная магнитная цепь
В качестве источника магнитного поля обычно применяется катушка с числом витков w1 , по которой протекает ток I.
Обмотка с током возбуждает магнитное поле и характеризуется магнитодвижущей силой (МДС)
Где: F – магнитодвижущая сила, А
I — сила тока, А
w – количество витков катушки.
Единицей МДС является ампер (А), еще эту единицу называют ампер-виток.
В магнитной цепи МДС играет такую же роль, как ЭДС в электрической.
Проводя аналогию с электрической цепью, отметим, что в магнитной цепи магнитопровод играет роль проводов, а роль нагрузки играет, как правило, воздушный зазор, в котором для функционирования устройства необходимо создать определенное магнитное поле.
Магнитная цепь может быть неразветвленной (см. рис. 25.1)и разветвленной (см. рис. 25.2).
Рис.26.2. Разветвленная магнитная цепь
Реальная магнитная цепь характеризуется не только магнитным потоком Ф, протекающим по магнитопроводу, но и потоками рассеяния Ф„ а также выпучиванием магнитных силовых линий в области воздушного зазора.
Обычно при анализе магнитных цепей пользуются следующими допущениями: индукция В принимается постоянной по сечению; пренебрегают потоками рассеяния и выпучиванием; вводят среднюю длину различных участков магнитопровода.
Узнать еще:
Топологическая оптимизация магнитной цепи громкоговорителя
В 1970-1980 годах музыкальные фанаты выделяли отдельные целые комнаты в домах под акустические стереосистемы. Громкоговорители в больших корпусах были важной частью этих систем. В настоящее время появилась новая тенденция — потребители хотят покупать мощные, но портативные колонки с возможностью подключения, как к проводным, так и беспроводным устройствам. Для проектирования современных лёгких колонок необходимо оптимизировать топологию их компонентов, и в частности магнитную систему динамика.
Портативность и разработка громкоговорителей
В настоящее время динамики обладают широкими возможностями подключения и улучшенным частотным диапазоном. Это позволяет синхронизировать их с виртуальными помощниками, передавать музыку по беспроводной связи и подключать дополнительные устройства, например, сабвуферы. Новый функционал подразумевает новые требования к конструкции. К примеру, некоторые колонки являются водонепроницаемыми для возможного использования в душе или в бассейне. Возможно, более серьёзными требованиеми являются долговечность и износостойкость устройства наряду с возможностью его использования прямо из коробки.
Слева: Колонка примерно 1980-х годов без защитной решётки. Изображение предоставлено PT35& — собственное произведение. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons. Справа: Пример современной, портативной колонки с беспроводной технологией поключения по Bluetooth®. Изображение предоставлено [email protected]. — собственное произведение. Доступно по лицензии CC BY-SA 2.0 на Flickr Creative Commons.
На данный момент, портативность — одно из самых важных пользовательских требований к дизайну аудиосистем различного класса. Таким образом, в настоящее время целью инженеров является разработка маленьких и лёгких колонок, которые в то же время должны обладать высоким качеством звучания и хорошими рабочими характеристиками. Чтобы максимально улучшить производительность при минимизации общего веса, можно оптимизировать топологию различных компонентов магнитной системы динамика, используя модуль Оптимизация (Optimization Module) в программном обеспечении COMSOL Multiphysics®.
Оптимизация конструкции магнитной цепи с использованием COMSOL Multiphysics®
В динамике магнитная цепь создаёт направленный магнитный поток в воздушном зазоре. Катушка механически соединяется с диафрагмой, которая перемещается перпендикулярно силовым линиям магнитного поля, и располагается в воздушном зазоре. Когда ток протекает по катушке, электромагнитная сила приводит её в движение. Диафрагма повторяет эти колебания, взаимодействуя с воздухом и создавая звуковые волны.
Магнитная цепь состоит из железного сердечника, который выполняет две важные функции:
- Увеличивает магнитный поток в катушке
- Обеспечивает однородное магнитное поле по всей длине катушки
В нашем случае геометрия практически аналогична учебному примеру Loudspeaker Driver model (Модель электродинамического громкоговорителя). В данной задаче материальную модель для железа можно задать через нелинейную относительную магнитную проницаемость \mu_r(B), полученную из кривой намагничивания BH. Это откроет возможность проведения именно топологической оптимизации, т.к. относительную проницаемость можно легко связать с т.н. полем контрольной переменной (control variable field), что требуется для настройки данного типа оптимизации.
Для нахождения оптимальной формы железного сердечника можно использовать топологическую оптимизацию.
Стандартным показателем оценки магнитной цепи является параметр BL или коэффициент электромеханической связи, который равен произведению магнитной индукции в воздушном зазоре на длину катушки. Чем больше параметр BL, тем выше производительность магнитной цепи. В рамках многокритериальной оптимизации можно проводить расчет оптимальной формы компонента как функции от параметра BL при условии уменьшения веса сердечника.
После решения задачи по нахождению оптимальной топологии, можно будет извлечь оптимизированную геометрию и использовать её для дальнейшего анализа.
Расчет рабочих характеристики и проектирование магнитной цепи
Исходная геометрия включает домен с сердечником, объем которого равен 37 см3 (речь идет о нижней части ярма). В первых двух исследованиях рассматриваемой модели проводится расчет магнитных полей для изначальной (относительно оптимальной) конфигурации цепи, а также обосновывается корректность использования методики с заданием нелинейной относительной проницаемости вместо стандартной кривой намагничивания B-H.
Слева: Исходная геометрия (красным цветом показано железо, синим — воздух). Справа: Норма магнитной индукции и силовые линии для начальной конфигурации.
Топологическая оптимизация магнитной цепи
Используя интерфейс Optimization (Оптимизация), вы можете ещё больше уменьшить объём железного сердечника, сохранив при этом его магнитные характеристики.
Третье исследование начинается с двухэтапной оптимизации: поддерживать максимально возможное значение BL, начиная с геометрии сердечника в виде «полного» цилиндра объёмом 52 см3. Первое условие задаётся как интегральная целевая функция (integral objective) по домену с Coil (Катушкой). Второе – интегральным ограничением в виде неравенства (integral inequality constraint), которое будет контролировать, чтобы объём сердечника оставался как можно ближе к заданному значению.
Цель Study 3 — cокращение объёма до 37 см3, и его результат, очень близкий к исходной геометрии, подтверждает, что исходная геометрия была практически оптимальной. В Study 4 решается задача оптимизации и поиска лучшей в плане производительности конфигурации при дальнейшем уменьшении объёма вдвое, примерно до 26 см3.
Слева: Оптимизированная геометрия, в которой объём железного сердечника равен 26 см3. Справа: Норма магнитной индукции и силовые линии для оптимизированный конфигурации.
Результаты двух исследований сопоставимы. Несмотря на то, что во втором случае объём меньше, это не влияет на рабочие характеристики системы.
Трёхмерный график (полученный разворотом исходных данный с осевой симметрией) нормы магнитной индукции окончательной оптимизированной геометрии.
Данные исследования показывают, что топологическая оптимизация может использоваться для определения наилучших параметров конфигурации динамика при учете необходимых ограничений.
Для дальнейшего анализа полученной конфигурации, окончательная оптимизированная форма может быть экспортирована как независимая геометрия.
Слева: Контурный график предельных оптимизированных геометрических размеров железа/воздуха. Справа: Оптимизированная форма, импортированная, как геометрический объект.
Дальнейшие шаги
Нажмите на кнопку ниже, чтобы скачать учебную модель и самостоятельно попрактиковаться в топологической оптимизации магнитной цепи. Вы перейдете в Галерею моделей и приложений. И если у вас есть учетная запись COMSOL Access и действующая лицензия на программное обеспечение, то вы можете скачать MPH-файл.
Узнайте больше о топологической оптимизации:
Товарный знак Bluetooth является зарегистрированной торговой маркой компании Bluetooth SIG, Inc., любое использование такого знака компанией COMSOL осуществляется по лицензии.
10.3: Магнитные цепи — Разработка LibreTexts
Магнитные цепи включают такие приложения, как трансформаторы и реле. Очень простая магнитная цепь показана на рисунке \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \): Простая магнитная цепь.
Во-первых, он состоит из магнитопровода. Сердечник может состоять из одного материала, такого как листовая сталь, но также может использовать несколько секций и воздушный зазор (и). Вокруг сердечника находится по крайней мере один набор витков провода, т.е.е., катушка, сформированная вокруг сердечника. Для трансформаторов используется несколько наборов витков (в простейшем случае один для первичной обмотки, а другой для вторичной). Как мы уже видели, прохождение тока через обмотки создает магнитный поток \ (\ Phi \) в сердечнике. Поскольку этот поток ограничен площадью поперечного сечения сердечника \ (A \), мы можем получить плотность потока \ (B \).
\ [B = \ frac {\ Phi} {A} \ label {10.4} \]
Где
\ (B \) — плотность магнитного потока в теслах,
\ (\ Phi \) — магнитный поток в веберах,
\ (A \) — площадь в квадратных метрах.
Вспомните из главы 9, что одна тесла определяется как один вебер на квадратный метр. Альтернативной единицей измерения, которая иногда используется, является гаусс (система единиц cgs), названная в честь Карла Фридриха Гаусса, немецкого математика и ученого.
\ [1 \ text {тесла} = 10 000 \ text {gauss} \ label {10.5} \]
Пример \ (\ PageIndex {1} \)
Магнитный поток паутины 6E-5 существует в сердечнике, поперечное сечение которого имеет размеры 1 на 2 сантиметра. Определите плотность потока в теслах.2} \ nonumber \]
\ [B = 0,3T \ nonumber \]
10.3.1: Закон Ома для магнитных цепей (закон Гопкинсона или Роуленда)
Между магнитными и электрическими цепями проводится общая параллель, а именно закон Гопкинсона (закон Роуленда). Для электрических цепей закон Ома гласит:
\ [V = I R \ nonumber \]
Аналогично для магнитных цепей:
\ [\ boldsymbol {F} = \ Phi \ boldsymbol {R} \ label {10.6} \]
Где
\ (\ boldsymbol {F} \) — магнитодвижущая сила (или MMF) в ампер-витках,
\ (\ Phi \) — магнитный поток в веберах,
\ (\ boldsymbol {R} \) — сопротивление материала в ампер-витках / Вебере.
Магнитодвижущая сила сравнивается с напряжением источника или электродвижущей силой (ЭДС), магнитный поток сравнивается с потоком тока, а реактивное сопротивление заменяет сопротивление (то есть, с одной стороны, у нас есть материал, который сопротивляется потоку ток, а с другой стороны, материал, у которого есть «сопротивление» для установления магнитного потока). Кроме того, магнитодвижущая сила — это произведение тока, протекающего через катушку, и количества витков или витков в катушке:
\ [\ boldsymbol {F} = N I \ label {10.7} \]
Где
\ (\ boldsymbol {F} \) — магнитодвижущая сила в ампер-оборотах,
\ (N \) — количество витков или витков в катушке,
\ (I \) — ток в катушке в амперах.
Уравнение сопротивления имеет хорошую параллель с уравнением сопротивления (уравнение 2.11 из главы 2):
\ [R = \ frac {\ phi l} {A} \ nonumber \]
\ [\ boldsymbol {R} = \ frac {l} {\ mu A} \ label {10.8} \]
Где
\ (\ boldsymbol {R} \) — сопротивление в ампер-витках / по Веберу,
\ (l \) — длина материала в метрах,
\ (A \) — площадь поперечного сечения материала в квадратных метрах,
\ (\ mu \) — проницаемость материала в генри / метр.
Учитывая характеристики катушки и длину пути магнитной цепи, магнитный поток приводит к возникновению намагничивающей силы \ (H \).
\ [H = \ frac {N I} {l} \ label {10.9} \]
Где
\ (H \) — сила намагничивания в ампер-витках / метр,
\ (N \) — количество витков или витков в катушке,
\ (I \) — ток катушки в амперах,
\ (l \) — длина магнитного пути в метрах.
Уравнение \ ref {10.8} показывает, что ферромагнитные материалы (то есть материалы с высокой проницаемостью, такие как сталь) имеют низкое сопротивление. Практическая проблема здесь в том, что \ (\ mu \), в отличие от удельного сопротивления \ (\ rho \) резисторов, не является постоянной величиной для таких материалов. Он может значительно различаться, как видно на общей диаграмме, представленной на рисунке \ (\ PageIndex {2} \). В результате нецелесообразно находить сопротивление таким же образом, как мы находим сопротивление. Однако еще не все потеряно.
Рисунок \ (\ PageIndex {2} \): Типичная кривая проницаемости для материала с высокой проницаемостью.
Плотность магнитного потока и соответствующая сила намагничивания для любого данного материала связаны следующим уравнением:
\ [B = \ mu H \ label {10.10} \]
Где
\ (B \) — плотность потока в теслах,
\ (\ mu \) — проницаемость материала в генри / метр,
\ (H \) — сила намагничивания в ампер-витках / метр.
Еще раз, сложность здесь — проницаемость материала керна. Для воздуха мы можем использовать проницаемость свободного пространства \ (\ mu_0 \).{-6} H / m \ label {10.11} \]
Для других материалов, таких как листовая или литая сталь, мы пойдем другим путем; а именно кривую, полученную эмпирическим путем, которая отображает зависимость плотности потока \ (B \) от силы намагничивания \ (H \). Такие графы обычно называют «кривыми \ (BH \)». Пример показан на рисунке \ (\ PageIndex {3} \). Ясно, что эта кривая не является хорошей прямой линией или даже очевидной предсказуемой функцией. Сразу заметные признаки — это начальный крутой подъем, за которым следует сглаживание кривой.Это сплющивание соответствует насыщению магнитного материала. Напротив, график для воздуха покажет прямую линию с очень пологим уклоном. Как мы увидим, возможность достичь высокой плотности магнитного потока для данной силы намагничивания приведет к созданию эффективной и действенной магнитной цепи. Таким образом, хотя воздух обладает положительным свойством ненасыщения, результирующая плотность потока низкая, что обычно приводит к снижению производительности.
Рисунок \ (\ PageIndex {3} \): Общая кривая \ (BH \).
10.3.2: Кривая BH
Процесс создания кривой \ (BH \) выглядит следующим образом. Сначала мы создаем ядро исследуемого материала. Затем вокруг этого сердечника наматывается катушка с проволокой. Пример показан на рисунке \ (\ PageIndex {4} \). Здесь у нас есть базовый тороид с катушкой на \ (N \) витков.
Рисунок \ (\ PageIndex {4} \): Тороидальный сердечник с катушкой.
Начнем с того, что система находится в состоянии покоя и не находится под напряжением. На катушку подается небольшой ток \ (I \).Это создает намагничивающую силу согласно уравнению \ ref {10.9}. Будет соответствующая плотность потока в соответствии с Уравнением \ ref {10.10}.
Затем ток увеличивается. Это приводит к увеличению силы намагничивания и соответствующему изменению плотности магнитного потока. Сила тока увеличивается до тех пор, пока кривая не станет плоской, указывая на то, что насыщение достигнуто. Эта траектория показана пунктирной линией на рисунке \ (\ PageIndex {5} \), начиная с точки \ (\ boldsymbol {a} \) с точкой \ (\ boldsymbol {b} \), обозначающей насыщение.Затем ток снижается. Это вызывает уменьшение намагничивающей силы, но, хотя плотность магнитного потока уменьшается, она не возвращается идеально по исходной траектории. Вместо этого кривая смещается над исходной.
Рисунок \ (\ PageIndex {5} \): Построение кривой BH.
В конце концов, ток упадет до нуля. Это соответствует точке \ (\ boldsymbol {c} \) на графике на рисунке \ (\ PageIndex {5} \). В этот момент, даже если в катушке нет тока, в сердечнике все еще есть магнитный поток.Результирующая магнитная индукция называется удерживающей способностью и является мерой остаточного магнетизма. Это явление позволяет намагничивать материалы.
Если мы теперь изменим направление тока катушки и начнем увеличивать его величину, плотность потока будет продолжать падать. В точке \ (\ boldsymbol {d} \) он достигнет нуля. Поскольку мы фактически принудили поток обратно к нулю, мы называем намагничивающую силу, необходимую для этого, коэрцитивной силой или коэрцитивной силой.
По мере увеличения величины тока плотность потока также увеличивается, но с противоположным знаком. В конце концов, в точке \ (\ boldsymbol {e} \) снова достигается насыщение. Еще раз, если величина тока уменьшается, величина плотности потока также будет уменьшаться, но не будет точно прослеживаться вдоль исходной траектории. На этот раз он пойдет по более низкому пути. Когда ток снижается до нуля в точке \ (\ boldsymbol {f} \), сохраняемость зеркала становится очевидной. Дальнейшее положительное увеличение тока показывает зеркальную коэрцитивность в точке \ (\ boldsymbol {g} \).Наконец, когда ток увеличивается до максимума, мы снова достигаем насыщения в точке \ (\ boldsymbol {b} \).
Если ток снова переключается таким образом, процесс повторяется, и снова выбирается внешний путь, указанный стрелками. Таким образом, конкретное значение силы намагничивания может привести к различным значениям плотности потока: это зависит от недавней истории материала. Этот эффект известен как гистерезис и встречается также в других областях.
Фактически, опубликованные кривые \ (BH \) следуют за серединой петли гистерезиса.Пример кривых \ (BH \) для трех различных материалов сердечника показан на рисунке \ (\ PageIndex {6} \) 1 . Кривая A — для листовой стали (которая обычно используется в трансформаторах), кривая B — для литой стали, а кривая C — для чугуна. Мы будем использовать их в следующих примерах. Также доступны кривые для других материалов.
Рисунок \ (\ PageIndex {6} \): Кривые BH для: A. Листовой стали B. Литой стали C. Чугуна
Пример \ (\ PageIndex {2} \)
Предположим, что тороид на рисунке \ (\ PageIndex {4} \) изготовлен из литой стали, имеет катушку на 500 витков, поперечное сечение 2 см на 2 см и среднюю длину пути 50 см.Определите магнитный поток в паутине, если на катушку подается ток 0,3 ампер.
Мы будем использовать уравнение \ ref {10.9}, чтобы найти силу намагничивания, и по кривой \ (BH \) найти плотность потока.
\ [H = \ frac {N I} {l} \ nonumber \]
\ [H = \ frac {500 \ text {повороты} \ times 0,3 A} {0,5 м} \ nonumber \]
\ [H = 300At / m \ text {(ампер-оборотов на метр)} \ nonumber \]
Литая сталь соответствует кривой B (зеленая) на рисунке \ (\ PageIndex {5} \). Приличная оценка плотности потока — 0.2 \ nonumber \]
\ [\ Phi = 2.08E-4Wb \ nonumber \]
10.3.3: KVL для магнитных цепей
Беглый просмотр уравнений \ ref {10.7} и \ ref {10.9} показывает, что:
\ [\ boldsymbol {F} = H l = N I \ label {10.12} \]
Продолжая аналогию с законом Ома, произведение ампер-витков катушки, \ (NI \), аналогично увеличению напряжения. Далее, произведение \ (Hl \) аналогично падению напряжения. Если мы затем расширим аналогию, включив в нее концепцию закона напряжения Кирхгофа, неудивительно, что сумма «подъемов» \ (NI \) должна равняться сумме «падений» \ (Hl \).В схеме на рисунке \ (\ PageIndex {4} \) есть один «подъем» и один «спад». Таким образом, магнитная цепь аналогична минимальной электрической цепи, показанной на рисунке \ (\ PageIndex {7} \). \ (\ boldsymbol {F} \) — магнитодвижущая сила, \ (NI \), а \ (\ boldsymbol {R} \) — сопротивление тороидального сердечника. Это сопротивление испытает «падение» \ (Hl \).
Рисунок \ (\ PageIndex {7} \): Аналог электрической схемы для магнитной системы на рисунке \ (\ PageIndex {4} \).
Ядро может состоять из двух или более разных материалов, что эквивалентно последовательной цепи. В этом случае таблица, подобная той, что представлена на рисунке \ (\ PageIndex {8} \), может использоваться для помощи в вычислениях. В этой таблице каждому разделу ядра соответствует отдельная строка. Стол разделен на две стороны (обратите внимание на толстую разделительную линию в центре). В общем, мы будем работать над проблемами, когда мы знаем данные с левой стороны и нам нужно найти что-то с правой стороны, или наоборот.Мост между двумя сторонами (т. Е. Пересекающий толстую линию) представляет собой кривую \ (BH \) для материала этого конкретного участка. Исключение из этого правила — если секция представляет собой воздушный зазор. В этом случае мы можем использовать определение \ ref {10.11}, которое показывает, что для воздуха \ (H \ приблизительно 7.958E5 B \) или, альтернативно, \ (B \ приблизительно 1.257E − 6 H \).
| Раздел | Флюс \ (\ Phi \) (Wb) | Площадь \ (А \) (т \ (^ 2 \)) | Плотность потока Б (Т) | Сила намагничивания \ (H \) (Ат / м) | Длина \ (длина \) (м) | «Капля» \ (Hl \) (At) |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 |
Рисунок \ (\ PageIndex {8} \): Формат таблицы, используемый для анализа магнитной цепи.2\))»> 1E − 4
Это «падение» составляет 22,8 ампер-витков, а катушка имеет 200 витков. Следовательно, требуемый ток:
\ [I = \ frac {H l} {N} \ nonumber \]
\ [I = \ frac {22.8At} {200 т} \ nonumber \]
\ [I = 114 мА \ nonumber \]
Далее рассмотрим ядро с двумя секциями.
Пример \ (\ PageIndex {4} \)
Учитывая магнитную систему, показанную на рисунке \ (\ PageIndex {10} \), предположим, что секция A изготовлена из листовой стали, а секция B — из литой стали.Каждая часть имеет сечение 2 см на 2 см. Длина пути A составляет 12 см, а длина пути B — 4 см. Если катушка имеет 50 витков, определите ток катушки, необходимый для достижения магнитного потока 2E-4.
Рисунок \ (\ PageIndex {10} \): Магнитная система для примера \ (\ PageIndex {4} \).
Аналогичная схема состоит из одного источника и двух сопротивлений. Это показано на рисунке \ (\ PageIndex {11} \).
Следовательно:
\ [N I = H_ {лист} l_ {лист} + H_ {cast} l_ {cast} \ nonumber \]
В нашей таблице будет две строки, одна для листовой стали, а вторая для литой стали.Первая строка потребует использования кривой A (листовая сталь) из рисунка \ (\ PageIndex {6} \), а вторая строка потребует использования кривой B (литая сталь).
Рисунок \ (\ PageIndex {11} \): Аналогичная электрическая схема для системы, показанной на рисунке \ (\ PageIndex {10} \).
Поток, как и ток в последовательном контуре, будет одинаковым в обеих секциях. Отсюда мы можем заполнить ряд других значений в таблице, чтобы получить:
| Раздел | Флюс \ (\ Phi \) (Wb) | Площадь \ (А \) (т \ (^ 2 \)) | Плотность потока Б (Т) | Сила намагничивания \ (H \) (Ат / м) | Длина \ (длина \) (м) | «Капля» \ (Hl \) (At) | |
|---|---|---|---|---|---|---|---|
| Листовая сталь | 2E − 4 | 4E − 4 | 0.2\))»> 4E − 4 | 0,5 | 290 | 0,04 | 11,6 |
Используя нашу аналогию с KVL, общее «падение» составляет 8,4 при + 11,6 ат, или 20 ампер. Катушка была указана как имеющая 50 витков. Следовательно:
\ [I = \ frac {H l} {N} \ nonumber \]
\ [I = \ frac {20 At} {50 т} \ nonumber \]
\ [I = 400 мА \ nonumber \]
Обратите внимание, что даже несмотря на то, что секция из литой стали короче секции из листовой стали, она дает большую «каплю»; точно так же, как резистор большего размера в электрической цепи.Это требует большего тока в катушке, чем если бы весь сердечник был сделан из листовой стали.
Наконец, должно быть очевидно, что потребление тока можно уменьшить, если у катушки будет больше витков. Здесь есть практический предел, потому что все витки должны входить в отверстие сердечника. Когда это пространство заполнится, единственный способ увеличить количество витков — использовать провод более тонкого сечения, но это увеличивает сопротивление провода и потери мощности, а также снижает максимальную допустимую нагрузку по току.
10.3.4: Обработка воздушных зазоров
В некоторых системах в сердечнике имеется воздушный зазор. Если для остатка остается только один материал, это создаст систему, подобную изображенной на рисунке \ (\ PageIndex {12} \). Основное наблюдение здесь заключается в том, что проницаемость воздуха намного ниже, чем у ферромагнитных материалов, и, таким образом, зазор будет иметь относительно большое сопротивление по сравнению с длиной его пути. Тогда возникает очевидный вопрос: зачем нам использовать пробел? Одна из возможностей — электромагнитное реле, внутреннее устройство которого показано на рисунке \ (\ PageIndex {13} \).
Рисунок \ (\ PageIndex {12} \): Аналогичная электрическая схема для системы с воздушным зазором.
Рисунок \ (\ PageIndex {13} \): Внутреннее устройство электрического реле.
Чтобы создать реле, мы помещаем одну часть сердечника на шарнир, который можно удерживать в открытом положении с помощью небольшой пружины. Это создает воздушный зазор (непосредственно слева от сердечника на рисунке). Если мы подадим достаточно большой ток, результирующего магнитного потока будет достаточно, чтобы преодолеть натяжение пружины и закрыть вторую деталь на первой (т.е., магнитное притяжение). Как только это происходит, зазор исчезает, уменьшая сопротивление вокруг петли. Система будет оставаться закрытой до тех пор, пока ток катушки не будет отключен и восстанавливающая пружина снова не разорвет две части. Мы добавляем изолированные металлические контакты к движущейся секции, и в итоге мы получаем сверхмощный выключатель, который «приводится в действие» управляющим током, а не механическим рычагом, перемещаемым человеком.
Стоит повторить, что для воздушных зазоров вместо кривой \ (BH \) мы можем использовать Определение \ ref {10.2 \). Длина пути основного сердечника составляет 8 см, а длина пути зазора составляет 1 мм. Сколько витков потребуется катушке, чтобы при токе катушки 400 мА достигнуть магнитного потока 1,2E-4?
Рисунок \ (\ PageIndex {14} \): Магнитная система для примера \ (\ PageIndex {5} \).
Аналогичная схема состоит из одного источника и двух сопротивлений, одно для сердечника из листовой стали, а второе для воздушного зазора. Это показано на рисунке \ (\ PageIndex {12} \). Далее аналогичное соотношение KVL:
\ [N I = H_ {лист} l_ {лист} + H_ {пробел} l_ {пробел} \ nonumber \]
В этой таблице будет две строки, одна для сердечника из листовой стали и одна для воздушного зазора.2 \))
Плотность потока
Б (Т)
Сила намагничивания
\ (H \) (Ат / м)
Длина
\ (длина \) (м)
«Капля»
\ (Hl \) (At)
Используя нашу аналогию с KVL, находим:
\ [N_2 I_2 = N_1 I_1 −H_ {лист} l_ {лист} \ nonumber \]
\ [N_2 I_2 = 2000 \ text {повороты} \ раз 120 мА −20 При \ nonumber \]
\ [N_2 I_2 = 240At −20 At \ nonumber \]
\ [N_2 I_2 = 220At \ nonumber \]
Катушка 2 была определена как имеющая 500 витков, следовательно, ее ток равен:
.
\ [I_2 = \ frac {220 At} {500 витков} \ nonumber \]
\ [I_2 = 440 мА \ nonumber \]
Ключевым моментом является то, что предыдущий пример должен использовать переменный ток, чтобы функционировать, как описано.Постоянный ток не даст ожидаемых результатов. Причина этого восходит к определению 10.2.1 и уравнению 10.2.2: если поток не изменяется относительно проводящей катушки, в катушке не будет индуцироваться напряжение. Таким образом, хотя входной постоянный ток будет создавать поток в сердечнике, этот поток будет статическим и неизменным. Следовательно, вторая катушка не будет производить выходной сигнал. Напротив, переменный ток плавно изменяется по амплитуде и полярности. Это создает плавно изменяющийся магнитный поток, который, в свою очередь, позволяет индуцировать напряжение во второй катушке.
Предположим на мгновение, что в предыдущем примере использовался переменный ток, обратите внимание, что ток почти в четыре раза выше в катушке 2, чем в катушке 1. Если бы мы смогли уменьшить «падение» сердечника до нуля, возможно, за счет уменьшения сопротивления сердечника до пренебрежимо малого значения, то ток увеличился бы ровно в четыре раза (до 480 мА против 440 мА). Это то же самое, что отношение количества витков катушки один к количеству витков катушки два, и известно как отношение витков.Это ключевой параметр, описывающий трансформаторы, который как раз и является предметом следующего раздела.
Магнитная цепь
Магнитный поток ф г , который проходит через воздушный зазор в структуре, показанной на рисунке 4.2, представляет собой часть общего потока, генерируемого током, протекающим в катушке, окружающей материал сердечника.
Этот полный поток ф, который проходит через замкнутую в катушку площадь поперечного сечения, создается током катушки и пропорционален как величине тока катушки i, так и общему количеству витков N провода, составляющего катушку.Произведение N и i называется магнитодвижущей силой катушки. Коэффициент пропорциональности в соотношении между общим магнитным потоком, создаваемым током катушки и mmf катушки, имеет единицы магнитного потока (измеренные в веберах) на единицу mmf (измеренные в ампер-витках).
Поскольку полный поток ф пропорционален силовому члену — ммс, — можно провести простую аналогию между магнитной цепью и электрической цепью. В электрической цепи постоянного тока ток i течет за счет электродвижущей силы (ЭДС) E.Закон Ома для электрической цепи гласит, что
где R — сопротивление цепи протеканию тока. Тогда «закон магнитного Ома» равен
.
где R — сопротивление магнитной цепи потоку магнитного потока. Этому сопротивлению потоку R было присвоено специальное название, чтобы отличать его от сопротивления потоку тока. Мы называем это сопротивлением магнитной цепи.
Сопротивление магнитной цепи будет приблизительно постоянным, пока плотность потока в любой части цепи ниже плотности потока насыщения для этой части цепи.Ферромагнитные материалы насыщаются магнитным потоком на уровнях плотности приблизительно 1-2 Тесла = 1-2 Вебера / (метр) 2 . На уровнях плотности, близких к этому значению насыщения, эффективное сопротивление материала быстро возрастает. На уровнях плотности ниже значения насыщения сопротивление ферромагнитных элементов намного ниже, чем у элементов сопоставимого размера, построенных из немагнитных материалов.
Построить представление простой сосредоточенной магнитной цепи для структуры магнитного выключателя, показанной на Рисунке 4.2, мы должны помнить, что полный поток, создаваемый катушкой, должен состоять из двух компонентов: составляющей зазора ф g , которая течет через катушку, структуры сердечника, якоря и зазора, и составляющей утечки ф ᵜ , который протекает через катушку, часть структуры сердечника и канал утечки воздуха. На рисунке 4.4a показаны два компонента, протекающие по их физическим путям.
На рисунке 4.4b показан электрический эквивалент «магнитной цепи» устройства.Здесь катушка mmf показана как источник постоянного напряжения величиной Ni, а магнитные сопротивления различных путей потока показаны как эквивалентные сопротивления.
Реактивная часть сердечника, которая несет как поток рассеяния, так и поток зазора, обозначена как R c ; сопротивление участка воздушного канала пути потока рассеяния обозначено как R ᵜ ; сопротивление сердечника и части якоря на пути потока зазора обозначено как R ca ; а реактивное сопротивление зазора обозначено как R g .Фактические значения сопротивлений R c , R ᵜ , R ca и R g определяются эффективными площадями поперечного сечения соответствующих путей потока, эффективной длиной соответствующих путей потока и магнитные проницаемости соответствующих путей потока. Если материалом пути является ферромагнитный материал, такой как железо, сопротивление пути также будет функцией уровня плотности потока внутри пути, если уровень плотности близок или превышает значение насыщения.
В общем, для любого заданного пути мы имеем сопротивление пути
, где L p — эффективная длина пути, A p — эффективная площадь поперечного сечения пути, а µ p — магнитная проницаемость среды пути. Если среда пути является ферромагнитной, при высоких уровнях потока на пути, ф p , поток, мы имеем µ p = µ p (ф p ). Поскольку поток в зазоре и поток утечки являются воздушными путями, оба пути проницаемости равны проницаемости свободного пространства µ o , что является строгой константой и не зависит от уровня потока в тракте.
Для разрыва имеем примерно
, где θ g — угловое раскрытие зазора, измеренное с якорем в его удерживаемом положении. Если мы определим
у нас тогда
Теперь из простого анализа цепи постоянного тока схемы на рис. 4.4b, мы имеем
или, если мы нормализуем сопротивление цепи как «видимое» из зазора, R ca + R ᵜ R c / (R ᵜ + R c ) до максимального сопротивления зазора R gmax , и назовем это отношение долей магнитного сопротивления кадра m, имеем
Поскольку сердечник и якорь изготовлены из магнитных материалов, в целом мы имеем
Этот последний результат предполагает, что доля магнитного сопротивления кадра m является небольшой величиной.Однако при высоких уровнях насыщения сердечника или якоря эти приближения становятся менее точными, и значение m будет расти. Некоторые устройства построены со стоимостью, рассчитанной на время, рэндов c рэнд. Для устройств, «спроектированных во времени», магнитное сопротивление на пути магнитного потока в сердечнике R c является высоким в течение некоторой части их рабочего времени. Таким образом, приведенные выше приближения также неверны.
Основы магнитной цепи
— ваше руководство по электрике
Замкнутый путь, по которому следует магнитный поток, известен как магнитная цепь .В магнитной цепи магнитный поток начинается из одной точки и заканчивается в той же точке. Магнитная цепь обычно состоит из магнитных материалов с высокой проницаемостью, таких как железо, мягкая сталь и т. Д., Поскольку они оказывают небольшое сопротивление магнитному потоку.
Магнитный поток обычно создается электрическим током через соленоид (имеющий большое количество витков. Существует три типа магнитных цепей:
- Магнитная цепь серии
- Параллельная магнитная цепь
- Последовательно-параллельные магнитные цепи
Магнитная цепь, состоящая из множества частей разных размеров и материалов, соединенных последовательно, называется последовательной магнитной цепью.
Рассмотрим составную магнитную цепь, состоящую из трех частей, имеющих разную длину, площадь поперечного сечения и относительную проницаемость. Он также имеет воздушный зазор.
В этом случае сопротивление каждой части будет различным в зависимости от размеров и относительной проницаемости этой части. Полное сопротивление будет суммой сопротивления отдельных частей. Один и тот же поток будет проходить через полные цепи.
Параллельная магнитная цепь
Магнитная цепь, которая имеет более одного пути для магнитного потока, называется параллельной магнитной цепью .Это похоже на параллельную электрическую цепь, в которой протекает более одного электрического тока.
Рассмотрим параллельную магнитную цепь, показанную на рисунке. На центральном плече намотана токоведущая катушка. Поток, создаваемый этой катушкой, делится в точке A на два пути, т.е.
- Flux ɸ 1 проходит по пути AFEB,
- Flux ɸ 2 проходит по пути ADCB
Очевидно, что = ɸ 1 + ɸ 2
Здесь два магнитных тракта AFEB и ADCB параллельны, общий MMF, необходимый для этой параллельной цепи, будет равен MMF, необходимому для любого из выше указанных путей.
Плотность магнитного потока (B)
Поток на единицу площади определяется как плотность магнитного потока . Он измеряется в плоскости, перпендикулярной потоку.
Плотность магнитного потока, B = φ ÷ A
Единицы: Вебер на квадратный метр ( Вт / м 2 ) или тесла (Тл).
Напряженность магнитного поля
Напряженность магнитного поля или напряженность магнитного поля определяется как MMF на единицу длины магнитной цепи.
Напряженность магнитного поля, H = (N I ) ÷ l
где N = количество витков намагничивающей катушки
I = ток через катушку
l = длина магнитного материала в метров
Единиц: ат / м.
Напряженность магнитного поля также известна как напряженность магнитного поля или сила намагничивания.
Проницаемость
Способность материала переносить магнитные линии потока известна как проницаемость этого материала.
Магнитные силовые линии могут очень легко проходить через материалы с высокой проницаемостью, такие как железо, сталь. Материалы с низкой проницаемостью, такие как дерево и т. Д., Не позволяют линиям потока легко проходить через них.
Абсолютная проницаемость
Это отношение плотности потока (B) в конкретной среде к напряженности магнитного поля (H), которое дает плотность магнитного потока. Обозначается µ.
Абсолютная проницаемость, µ = µ o µ r
Единицы: Генри / метр (Г / м)
Проницаемость воздуха / пространства / вакуума
Если оставить магнит в воздухе или в вакууме соотношение плотности потока (B) и напряженности магнитного поля (H) определяется как проницаемость свободного пространства.Обозначается µ o .
Проницаемость свободного пространства , µ o = 4π x 10 -7 Гн / м
Относительная проницаемость
Отношение проницаемости материала к проницаемости для вакуума или воздуха известно как относительная проницаемость .
Относительная проницаемость, µ r = µ ÷ µ o
Не имеет единиц .
Относительная проницаемость вакуума, воздуха и всех немагнитных материалов равна 1.Относительная магнитная проницаемость всех магнитных материалов очень высока. Например, относительная проницаемость пермаллоя (никель 78% и железо 22%) составляет около 50000.
Магнитодвижущая сила (MMF)
Магнитодвижущая сила — это движущая сила, которая создает магнитный поток. Напряженность магнитного поля (H) определяется MMF.
Магнитодвижущая сила, MMF = N I
где N = количество витков намагничивающей катушки
I = ток через катушку
Единицы: амперные витки ( AT )
(S)
Это противодействие потоку магнитного потока со стороны магнитного материала.
Единица: AT / Wb
Сопротивление, S = l ÷ (µ x a)
где l = длина магнитного пути в метрах.
a = площадь поперечного сечения магнитного пути в квадратном метре.
µ = абсолютная проницаемость среды в Гн / м.
= µ o µ r
Следовательно, сопротивление, S = l ÷ (µ o µ r a)
Сопротивление также определяется соотношением MMF и величиной потока. произведено.
то есть сопротивление, S = MMF ÷ поток
Reluctance, S = (N I ) ÷ φ
Permeance
Permeance of the материала представляет легкость, с которой может быть произведено из этого материала. Это обратная реакция на сопротивление. Его единица измерения — Wb / AT или генри.
Магнитная восприимчивость
Намагниченность материала пропорциональна полю, а константа пропорциональности называется магнитной восприимчивостью.Другими словами, его можно определить как отношение намагниченности M к силе намагничивания H , т.е.
Магнитная восприимчивость, X м = M / H
Это безразмерная величина. Это мера того, насколько легко материал намагничивается в намагничивающем поле. Его значение для вакуума равно нулю, поскольку в вакууме не может быть намагниченности.
Мы можем классифицировать материалы по X м . Материалы с положительными значениями X м являются парамагнитными, а материалы с отрицательными значениями X м — диамагнитными.Для ферромагнитных материалов X м является положительным и очень большим.
Поток утечки
Часть общего магнитного потока, протекающая через магнитную цепь, называется полезным магнитным потоком. Однако магнитный поток, который не полностью проходит через магнитный путь, а частично проходит через воздух, называется магнитным потоком рассеяния .
Математически, φ общий = φ полезный + φ утечка
Коэффициент утечки (λ)
Отношение общего производимого потока к полезному потоку называется коэффициентом утечки или коэффициентом утечки.
Коэффициент утечки, λ = φ общий / φ полезный
Значение коэффициента утечки всегда больше единицы. Типичные значения коэффициента утечки от 1,12 до 1,25. В магнитных цепях утечку магнитного поля можно минимизировать, разместив катушки возбуждения как можно ближе к точкам, в которых должен использоваться магнитный поток.
Окантовка
Магнитные силовые линии отталкиваются друг от друга, проходя через немагнитный материал.Из-за этого, когда силовые линии пересекают воздушный зазор, они имеют тенденцию выпирать наружу. Этот эффект известен как окантовка .
Эффект окантовки заключается в том, что эффективная площадь воздушного зазора становится больше, чем площадь магнитного пути, и, следовательно, плотность магнитного потока в воздушном зазоре уменьшается. Эффект окантовки зависит от длины воздушного зазора. Чтобы минимизировать образование бахромы, воздушный зазор должен быть как можно меньше. Эффектом окантовки можно пренебречь, если длина воздушного зазора очень мала по сравнению с его шириной.
Спасибо, что прочитали «Основы магнитной цепи».
Электромагнетизм | Все сообщения
Введение в магнитную цепь — узнайте все об этой основной силе и линиях потока
Магнитное поле
Прежде чем перейти к пониманию магнитной цепи, мы должны сначала понять, что подразумевается под магнитным полем. Теперь вы наверняка знаете, что если вы положите магнит на стол и поместите рядом с ним небольшой железный предмет, он просто приклеится к магниту.Сила, с которой тянется деталь, уменьшается по мере увеличения расстояния от магнита. Это явление можно объяснить, если учесть, что пространство вокруг магнита пронизано силой, которая воздействует на железный кусок рядом с ним. Это силовое поле известно как магнитное поле, которое можно визуализировать в форме магнитных линий потока. Это просто воображаемые линии, которые на самом деле не существуют, а могут быть только испытаны. На рисунке ниже показаны эти воображаемые линии магнитного потока, окружающие магнит.
Линии магнитной силы
Характеристики линий потока
Существуют следующие характеристики силовых линий.
Направление: любая линия потока всегда направлена на северный полюс магнита, при условии, что она не находится под влиянием другой магнитной среды, кроме магнитного поля Земли.
Замкнутая линия: все линии потока образуют замкнутую петлю, которая выходит из Северного полюса в Южный полюс магнита
Независимая область: линии потока никогда не пересекаются.
Отталкивание: силовые линии, направленные в одном направлении, всегда отталкивают друг друга.
Магнитная цепь
Приведенное выше обсуждение магнитного поля и силовых линий приводит нас к определению магнитной цепи. Магнитную цепь можно описать как полный замкнутый путь, за которым следует любая группа линий магнитного потока. Магнитная цепь очень похожа на электрическую цепь с точки зрения различных параметров, связанных с магнитной цепью, некоторые из которых описаны ниже.
Магнитодвижущая сила: так же, как электродвижущая сила или ЭДС заставляет электрический ток течь, аналогично магнитодвижущая сила или mmf делает возможным магнитный поток в магнитной цепи. Единицами измерения ммс являются ампер-витки, где витки означают количество витков электрической катушки, генерирующих это ммс. Поскольку количество членов является безразмерной величиной, фактически единицы измерения ммс совпадают с единицами измерения тока, а именно амперами.
Напряженность магнитного поля: это значение mmf, которое существует на единицу длины магнитной цепи при условии, что цепь однородна и имеет однородную площадь поперечного сечения.Раньше это также было известно как сила намагничивания, но сейчас этот термин устарел. Единицы измерения напряженности магнитного поля — амперы / метр.
Конечно, это всего лишь несколько основных концепций, связанных с магнитной цепью. Мы также узнаем больше об этом в разных статьях.
Магнитная цепь трансформатора
Магнитная цепь или сердечник трансформатора предназначены для создания пути для магнитного поля, которое необходимо для индукции напряжений между обмотками.Для этой цели используется путь с низким сопротивлением (т. Е. Сопротивления магнитным силовым линиям), состоящий из тонких кремниевых пластин из листовой стали. Сердечник не только обеспечивает путь для магнитного поля с низким сопротивлением, но и предотвращает циркуляцию электрических токов внутри самой стали. Циркуляционные токи, называемые вихревыми токами, вызывают нагревание и потерю энергии. Они возникают из-за напряжений, индуцированных в стали сердечника, которая постоянно подвергается воздействию переменных магнитных полей.Сама сталь является проводником, и изменяющиеся линии магнитного потока также вызывают в этом проводнике напряжение и ток. Использование очень тонких стальных листов с изоляционным материалом между листами значительно снижает вихревые токи (потери). Два общих расположения магнитного пути и обмоток показаны на Рис. 1 и Рис. 2 . В трансформаторе с сердечником (в форме сердечника) обмотки окружают сердечник.
Секция первичной и вторичной обмоток намотана на каждую ветвь сердечника, обмотка низкого напряжения намотана рядом с сердечником, а обмотка высокого напряжения намотана поверх низкого напряжения.
Изображение 1: Магнитные цепи
Изображение 2: Блоки трансформатора с трехфазным сердечником и трехфазным кожухом
В трансформаторе кожухового типа стальная магнитная цепь (сердечник) образует оболочку, окружающую обмотки. В форме сердечника обмотки находятся снаружи; в форме оболочки обмотки находятся внутри. В силовых трансформаторах электрические обмотки расположены так, что практически все магнитные силовые линии проходят как через первичную, так и через вторичную обмотки.Небольшой процент магнитных силовых линий выходит за пределы сердечника, и это называется потоком рассеяния. Более крупные трансформаторы, такие как трансформаторы Reclamation GSU, почти всегда имеют корпус.
Обратите внимание, что в трансформаторах в форме оболочки (см. Рисунок 2 ) магнитный поток, внешний по отношению к катушкам как на левом, так и на правом краях, имеет полные магнитные пути для паразитного потока и потока нулевой последовательности, чтобы вернуться к катушкам. В основной форме из рисунка легко видно, что как на левом, так и на правом крайнем положении нет обратных путей.Это означает, что флюс должен использовать внешние стенки резервуара и изолирующую среду для обратных путей. 2).
Зачем нужен воздушный зазор в магнитной цепи и как его рассчитать?
В этом блоге мы рассмотрим теорию воздушных зазоров в магнитных цепях. Магнитная цепь — это то место, где магнитный поток циркулирует или проходит через замкнутую область или путь. Воздушный зазор — это немагнитная часть магнитной цепи, и она обычно магнитно соединена последовательно с остальной частью цепи. Это позволяет значительной части магнитного потока проходить через зазор. В зависимости от применения воздушный зазор может быть заполнен немагнитным материалом, например газом, водой, вакуумом, пластиком, деревом и т. Д.и не обязательно только воздухом. Ну а какова функция воздушной прослойки?
Зачем нужен воздушный зазор в магнитной цепи?
Рассмотрим магнитную цепь с воздушным зазором, как показано ниже. Давайте обсудим различные причины, по которым воздушные зазоры имеют решающее значение в практических приложениях. В этой цепи есть только один путь для магнитной цепи, поэтому ее можно назвать последовательной магнитной цепью.
Рис. 1. Последовательная магнитная цепь с воздушным зазором
Одна из основных причин появления воздушного зазора — увеличение сопротивления магнитной цепи.Количество воздуха или другого немагнитного материала, такого как волокнистая пластина или волокнистая плита, увеличивает сопротивление цепи, тем самым увеличивая количество тока, который мы могли бы подать в катушку, прежде чем мы достигнем насыщения. Кроме того, воздушные зазоры помогают магнитному потоку расширяться за пределы магнитной цепи. Этот поток выходит в соседний воздушный канал, и такие пути потока называются потоком, что приводит к неоднородной плотности потока в воздушном зазоре. По мере увеличения воздушного зазора увеличивается магнитная окантовка, и наоборот.При небольших воздушных зазорах окантовкой можно пренебречь, если не указано иное. Однако с большим воздушным зазором нам, возможно, придется принять во внимание это изменение площади, когда мы начнем производить расчеты плотности потока.
Как рассчитать плотность потока в воздушном зазоре?
Давайте посмотрим на основную формулу для расчета плотности потока.
Плотность потока, B г = Φ г / A г
где, B — плотность магнитного потока в теслах (Тл)
Φ — магнитный поток в Веберсе (Вб)
A — площадь в квадратных метрах (m2)
Как мы знаем, проницаемость любого материала может быть выражена как отношение плотности магнитного потока к напряженности магнитного поля материала.Это может быть выражено следующим образом:
мк = B / H
где μ — проницаемость материала, Генри / метр
H — напряженность магнитного поля, ампер-виток / метр
B — плотность потока, тесла
Решая приведенное выше уравнение относительно B, получаем
B = μ x H… .. (Уравнение 1)
Теперь сила намагничивания воздушного зазора определяется следующим образом:
H = Fm / l….. (Уравнение 2)
где, Fm — магнитодвижущая сила (ммс), в ампер-витках, l — длина материала (зазора), в метрах
Подставляя значение H из уравнения 2 в уравнение 1, мы получаем
B = μ x (Фм / л)
Решая приведенное выше уравнение для магнитодвижущей силы, получаем
Fm = Bl / μ …….. (Уравнение 3)
Предположим, что у нас есть воздушный зазор, а проницаемость воздуха (свободного пространства) постоянна.
мкм воздух = 4π x 10 -7 Г / м
Заменяя значение μ в уравнении 3, мы получаем очень простую формулу для определения магнитодвижущей силы, необходимой для создания определенного потока в воздушном зазоре.
F м = BL / (4π x 10 -7 )
Воздушный зазор может иметь различную форму, форму и размер в зависимости от типа магнитной цепи и ее формы. В некоторых схемах он может быть неотъемлемой частью, обеспечивающей правильную работу устройства, но в других случаях он должен быть как можно меньше. Такие требования будут определяться принципом работы, производительностью, размером, эффективностью и многими другими технологическими факторами.
Мы надеемся, что это было полезно для вас, как для технического специалиста, или для студента, приступившего к работе.Если у вас есть какие-либо вопросы о программах по электронике или электромеханику, вы можете связаться с одним из наших консультантов по программе по бесплатному телефону 1-888-553-5333 или по электронной почте [email protected].
Магнитная цепь — точка назначения
Магнитная цепь
Определение
Магнитная цепь состоит из магнитных материалов с высокой проницаемостью, таких как железо, мягкая сталь и т. Д. Это замкнутый путь, за которым следуют магнитные линии сил называется магнитной цепью.В магнитной цепи магнитный поток или магнитная силовая линия начинается с точки и заканчивается в той же точке после завершения своего пути. Поток создается магнитами; это может быть постоянный магнит или электромагниты.
Концепция «магнитной цепи» использует взаимно однозначное соответствие между уравнениями магнитного поля в ненасыщенном ферромагнитном материале и уравнениями электрической цепи. Используя эту концепцию, можно быстро решить проблему магнитных полей сложных устройств, таких как трансформаторы, с помощью методов и технологий, разработанных для электрических цепей.
Магнитные цепи используются в различных устройствах, таких как электродвигатели, трансформаторы, реле, гальванометры генераторов и т. Д. Рассмотрим соленоид, имеющий N витков, намотанных на железный сердечник. Магнитный поток ø Weber устанавливается в сердечнике, когда через соленоид пропускается ток величиной I ампер.
Некоторые примеры магнитных цепей:
- Подковообразный магнит с железным держателем (цепь с низким сопротивлением)
- Подковообразный магнит без держателя (схема с высоким сопротивлением)
- Электродвигатель (контур переменного магнитного сопротивления)
Структура и функции магнитных цепей
В кольцевом электромагните с небольшим воздушным зазором магнитное поле или поток почти полностью ограничивается металлическим сердечником и воздушным зазором, которые вместе образуют магнитную цепь.В электродвигателе магнитное поле в значительной степени ограничено магнитными полюсными наконечниками, ротором, воздушными зазорами между ротором и полюсными наконечниками и металлической рамой. Каждая линия магнитного поля образует полную непрерывную петлю. Все линии вместе составляют общий поток. Если магнитный поток разделен так, что его часть ограничена одной частью устройства, а часть — другой, магнитная цепь называется параллельной. Если весь поток ограничен одним замкнутым контуром, как в кольцевом электромагните, цепь называется последовательной магнитной цепью.
Магнитный поток аналогичен электрическому току. Магнитодвижущая сила mmf аналогична электродвижущей силе и может считаться фактором, определяющим магнитный поток. MMF эквивалентен количеству витков провода, по которому проходит электрический ток, и имеет единицы ампер-витков. Если либо ток через катушку (как в электромагните), либо количество витков провода в катушке увеличивается, mmf больше; и если остальная часть магнитной цепи остается прежней, магнитный поток увеличивается пропорционально.
Магнитный поток через магнитный компонент пропорционален количеству силовых линий магнитного поля, которые проходят через площадь поперечного сечения этого компонента. Это чистое число, то есть число, проходящее в одном направлении, за вычетом числа, проходящего в другом направлении. Направление вектора магнитного поля B по определению находится от южного к северному полюсу магнита внутри магнита; за пределами линий поля идти с севера на юг.
Поток через элемент площади, перпендикулярной направлению магнитного поля, определяется произведением магнитного поля и элемента площади. В более общем смысле, магнитный поток Φ определяется скалярным произведением магнитного поля и вектора элемента площади.
Применение магнитной цепи
Магнитный поток первичной обмотки может возбуждать / индуцировать плотность магнитного потока в материале сердечника примерно в 10000 раз сильнее, чем в воздухе, и именно это позволяет преобразовывать энергию между электрические и магнитные поля.

