Open Library - открытая библиотека учебной информации. Неметрические шкалы
Неметрические шкалы
Измерительные шкалы
1.4.1 Шкала физической величины
Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на основании результатов точных измерений.
Например, международная температурная шкала, состоящая из ряда реперных точек, значения которых приняты по соглашению между странами Метрической Конвенции и установлены на основании точных измерений, предназначена служить исходной основой для измерений температуры
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом. В теории измерений различают пять основных типов шкал измерений:
- неметрические шкалы : шкалы наименований (классификации) и шкалы порядка;
- метрические шкалы : шкалы интервалов, шкалы отношений, абсолютные шкалы.
Неметрическими шкалами называютусловные шкалы физических величин, исходные значения которых выражены в условных единицах.
Шкалы наименований (классификации) используются для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета, марки автомобилей и т.п.
При большом числе классов используют иерархические шкалы наименований.
С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию - проверку их совпадения или несовпадения. По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа - критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам.
Примеры:
- системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение;
- цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета;
- многочисленные виды классификаций, которые существуют во многих разновидностях: например, с помощью диагностических средств классифицируют болезни, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
Номинальная шкала, используемая для классификации, называется шкалой классификации .
В шкале классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, – это отношение эквивалентности. Такие признаки удовлетворяют аксиомам тождества:
Либо А = В, либо А ≠ В;
Если А = В, то В = А;
Если А = В и В = С, то А = С.
Шкалы порядка (рангов) являются монотонно изменяющимися и позволяют установить отношение «больше – меньше» между величинами, характеризующими это свойство. Если для обозначения реперных точек используются цифры, то они называются баллами.
Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать, т.е. на шкале порядка не определены никакие математические операции.
В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего. Т.е. для любых чисел a, b и c таких, что a < b и b < c , справедливо соотношение a < c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко.
Пример - В образовательных учреждениях по шкале порядка, представленной в таблице 1.4, измеряются знания учащихся.
Таблица 1.4 – Сравнение российской и международной систем оценки знаний
| Российские оценки | ECTS | Смысловое содержание оценки |
| 5 | A | Отлично |
| 4 | B | Очень хорошо |
| C | Хорошо | |
| 3 | D | Удовлетворительно |
| E | Посредственно | |
| 2 | FX | Неудовлетворительно (с правом пересдачи) |
| * | F | Неудовлетворительно (без права пересдачи) |
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2 и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.
Упорядочение в шкале порядка может осуществляться по внешним признакам (нумерация) или по внутренним свойствам (ранжирование).
Примеры:
- нумерация мест в театрах, домов на улице, исследуемых образцов промышленных изделий и т.д.;
- ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов, представленная в таблице 1.5. В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.
Таблица 1.5 - Минералогическая шкала твёрдости
| Балл | Твёрдость |
| Меньше твёрдости талька | |
| Равна или больше твёрдости талька, но меньше твёрдости гипса | |
| Равна или больше твёрдости гипса, но меньше твёрдости извес ткового шпата | |
| Равна или больше твёрдости известкового шпата, но меньше твёрдости плавикового шпата | |
| Равна или больше твёрдости плавикового шпата, но меньше твёрдости апатита | |
| Равна или больше твёрдости апатита, но меньше твёрдости полевого шпата | |
| Равна или больше твёрдости полевого шпата, но меньше твёрдости кварца | |
| Равна или больше твёрдости кварца, но меньше твёрдости топаза | |
| Равна или больше твёрдости топаза, но меньше твёрдости корунда | |
| Равна или больше твёрдости корунда, но меньше твёрдости алмаза | |
| Равна твёрдости алмаза или больше её |
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным. Не все объекты можно подчинить отношению порядка. Например, нельзя сказать, что больше - круг или треугольник, но можно выделить в этих объектах общее свойство - площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы.
studlib.info
Неметрические шкалы
Образование Неметрические шкалы
просмотров - 52
Измерительные шкалы
1.4.1 Шкала физической величины
Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на основании результатов точных измерений.
К примеру, международная температурная шкала, состоящая из ряда реперных точек, значения которых приняты по соглашению между странами Метрической Конвенции и установлены на основании точных измерений, предназначена служить исходной основой для измерений температуры
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом. В теории измерений различают пять базовых типов шкал измерений:
- неметрические шкалы: шкалы наименований (классификации) и шкалы порядка;
- метрические шкалы: шкалы интервалов, шкалы отношений, абсолютные шкалы.
Неметрическими шкаламиназываютусловные шкалы физических величин, исходные значения которых выражены в условных единицах.
Шкалы наименований (классификации)используются для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета͵ марки автомобилей и т.п.
При большом числе классов используют иерархические шкалы наименований.
С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию - проверку их совпадения или несовпадения. По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа - критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам.
Примеры:
- системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение;
- цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета;
- многочисленные виды классификаций, которые существуют во многих разновидностях: к примеру, с помощью диагностических средств классифицируют болезни, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
Номинальная шкала, используемая для классификации, принято называть шкалой классификации.
В шкале классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, - ϶ᴛᴏ отношение эквивалентности. Такие признаки удовлетворяют аксиомам тождества:
Либо А = В, либо А ≠ В;
В случае если А = В, то В = А;
В случае если А = В и В = С, то А = С.
Шкалы порядка (рангов)являются монотонно изменяющимися и позволяют установить отношение «больше – меньше» между величинами, характеризующими это свойство. В случае если для обозначения реперных точек используются цифры, то они называются баллами.
Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать, ᴛ.ᴇ. на шкале порядка не определены никакие математические операции.
В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего. Т.е. для любых чисел a, b и c таких, что a < b и b < c , справедливо соотношение a < c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (ᴛ.ᴇ. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко.
Пример - В образовательных учреждениях по шкале порядка, представленной в таблице 1.4, измеряются знания учащихся.
Таблица 1.4 – Сравнение российской и международной систем оценки знаний
| Российские оценки | ECTS | Смысловое содержание оценки |
| 5 | A | Отлично |
| 4 | B | Очень хорошо |
| C | Хорошо | |
| 3 | D | Удовлетворительно |
| E | Посредственно | |
| 2 | FX | Неудовлетворительно (с правом пересдачи) |
| * | F | Неудовлетворительно (без права пересдачи) |
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2 и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.
Упорядочение в шкале порядка может осуществляться по внешним признакам (нумерация) или по внутренним свойствам (ранжирование).
Примеры:
- нумерация мест в театрах, домов на улице, исследуемых образцов промышленных изделий и т.д.;
- ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов, представленная в таблице 1.5. В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.
Таблица 1.5 - Минералогическая шкала твёрдости
| Балл | Твёрдость |
| Меньше твёрдости талька | |
| Равна или больше твёрдости талька, но меньше твёрдости гипса | |
| Равна или больше твёрдости гипса, но меньше твёрдости извес ткового шпата | |
| Равна или больше твёрдости известкового шпата͵ но меньше твёрдости плавикового шпата | |
| Равна или больше твёрдости плавикового шпата͵ но меньше твёрдости апатита | |
| Равна или больше твёрдости апатита͵ но меньше твёрдости полевого шпата | |
| Равна или больше твёрдости полевого шпата͵ но меньше твёрдости кварца | |
| Равна или больше твёрдости кварца, но меньше твёрдости топаза | |
| Равна или больше твёрдости топаза, но меньше твёрдости корунда | |
| Равна или больше твёрдости корунда, но меньше твёрдости алмаза | |
| Равна твёрдости алмаза или больше её |
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным. Не все объекты можно подчинить отношению порядка. К примеру, нельзя сказать, что больше - круг или треугольник, но можно выделить в этих объектах общее свойство - площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы.
Читайте также
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на... [читать подробенее]
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на... [читать подробенее]
oplib.ru
Неметрические шкалы
Образование Неметрические шкалы
просмотров - 52
Измерительные шкалы
1.4.1 Шкала физической величины
Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на основании результатов точных измерений.
К примеру, международная температурная шкала, состоящая из ряда реперных точек, значения которых приняты по соглашению между странами Метрической Конвенции и установлены на основании точных измерений, предназначена служить исходной основой для измерений температуры
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом. В теории измерений различают пять базовых типов шкал измерений:
- неметрические шкалы: шкалы наименований (классификации) и шкалы порядка;
- метрические шкалы: шкалы интервалов, шкалы отношений, абсолютные шкалы.
Неметрическими шкаламиназываютусловные шкалы физических величин, исходные значения которых выражены в условных единицах.
Шкалы наименований (классификации)используются для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета͵ марки автомобилей и т.п.
При большом числе классов используют иерархические шкалы наименований.
С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию - проверку их совпадения или несовпадения. По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа - критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам.
Примеры:
- системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение;
- цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета;
- многочисленные виды классификаций, которые существуют во многих разновидностях: к примеру, с помощью диагностических средств классифицируют болезни, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
Номинальная шкала, используемая для классификации, принято называть шкалой классификации.
В шкале классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, - ϶ᴛᴏ отношение эквивалентности. Такие признаки удовлетворяют аксиомам тождества:
Либо А = В, либо А ≠ В;
В случае если А = В, то В = А;
В случае если А = В и В = С, то А = С.
Шкалы порядка (рангов)являются монотонно изменяющимися и позволяют установить отношение «больше – меньше» между величинами, характеризующими это свойство. В случае если для обозначения реперных точек используются цифры, то они называются баллами.
Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать, ᴛ.ᴇ. на шкале порядка не определены никакие математические операции.
В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего. Т.е. для любых чисел a, b и c таких, что a < b и b < c , справедливо соотношение a < c (транзитивность). Эти свойства транзитивности означают, что на шкалах порядка определены (ᴛ.ᴇ. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко.
Пример - В образовательных учреждениях по шкале порядка, представленной в таблице 1.4, измеряются знания учащихся.
Таблица 1.4 – Сравнение российской и международной систем оценки знаний
| Российские оценки | ECTS | Смысловое содержание оценки |
| 5 | A | Отлично |
| 4 | B | Очень хорошо |
| C | Хорошо | |
| 3 | D | Удовлетворительно |
| E | Посредственно | |
| 2 | FX | Неудовлетворительно (с правом пересдачи) |
| * | F | Неудовлетворительно (без права пересдачи) |
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2 и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.
Упорядочение в шкале порядка может осуществляться по внешним признакам (нумерация) или по внутренним свойствам (ранжирование).
Примеры:
- нумерация мест в театрах, домов на улице, исследуемых образцов промышленных изделий и т.д.;
- ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов, представленная в таблице 1.5. В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.
Таблица 1.5 - Минералогическая шкала твёрдости
| Балл | Твёрдость |
| Меньше твёрдости талька | |
| Равна или больше твёрдости талька, но меньше твёрдости гипса | |
| Равна или больше твёрдости гипса, но меньше твёрдости извес ткового шпата | |
| Равна или больше твёрдости известкового шпата͵ но меньше твёрдости плавикового шпата | |
| Равна или больше твёрдости плавикового шпата͵ но меньше твёрдости апатита | |
| Равна или больше твёрдости апатита͵ но меньше твёрдости полевого шпата | |
| Равна или больше твёрдости полевого шпата͵ но меньше твёрдости кварца | |
| Равна или больше твёрдости кварца, но меньше твёрдости топаза | |
| Равна или больше твёрдости топаза, но меньше твёрдости корунда | |
| Равна или больше твёрдости корунда, но меньше твёрдости алмаза | |
| Равна твёрдости алмаза или больше её |
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным. Не все объекты можно подчинить отношению порядка. К примеру, нельзя сказать, что больше - круг или треугольник, но можно выделить в этих объектах общее свойство - площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы.
Читайте также
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на... [читать подробенее]
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на... [читать подробенее]
oplib.ru
Неметрические шкалы
Измерительные шкалы
1.4.1 Шкала физической величины
Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению на основании результатов точных измерений.
Например, международная температурная шкала, состоящая из ряда реперных точек, значения которых приняты по соглашению между странами Метрической Конвенции и установлены на основании точных измерений, предназначена служить исходной основой для измерений температуры
Шкалы измерений принято классифицировать по типам измеряемых данных, которые определяют допустимые для данной шкалы математические преобразования, а также типы отношений, отображаемых соответствующей шкалой. Современная классификация шкал была предложена в 1946 году Стэнли Смитом Стивенсом. В теории измерений различают пять основных типов шкал измерений:
- неметрические шкалы: шкалы наименований (классификации) и шкалы порядка;
- метрические шкалы: шкалы интервалов, шкалы отношений, абсолютные шкалы.
Неметрическими шкаламиназываютусловные шкалы физических величин, исходные значения которых выражены в условных единицах.
Шкалы наименований (классификации)используются для измерения значений качественных признаков. Значением такого признака является наименование класса эквивалентности, к которому принадлежит рассматриваемый объект. Примерами значений качественных признаков являются названия государств, цвета, марки автомобилей и т.п.
При большом числе классов используют иерархические шкалы наименований.
С величинами, измеряемыми в шкале наименований, можно выполнять только одну операцию - проверку их совпадения или несовпадения. По результатам такой проверки можно дополнительно вычислять частоты заполнения (вероятности) для различных классов, которые могут использоваться для применения различных методов статистического анализа - критерия согласия Хи-квадрат, критерия Крамера для проверки гипотезы о связи качественных признаков и др.
Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. Условные номера в качестве имен присваиваются по следующему правилу: нельзя присваивать одно имя (число) двум разным объектам.
Примеры:
- системы пожарной сигнализации вырабатывают сигнал «пожара нет», когда температура ниже определенного значения, и сигнал «пожар», когда температура превышает это значение;
- цвет любой вещи можно определить по названию подходящего цвета в атласе цветов, предназначенном для идентификации цвета;
- многочисленные виды классификаций, которые существуют во многих разновидностях: например, с помощью диагностических средств классифицируют болезни, проводят контроль изделий (классификация на годные и бракованные), осуществляют сложную процедуру распознавания образов и т.д.; наиболее известными примерами таких шкал являются шкалы, используемые для классификации животных и растений.
Номинальная шкала, используемая для классификации, называется шкалой классификации.
В шкале классификации существенно лишь то, что единственное отношение в системе объектов, передаваемое шкалой классификации, – это отношение эквивалентности. Такие признаки удовлетворяют аксиомам тождества:
Либо А = В, либо А ≠ В;
Если А = В, то В = А;
Если А = В и В = С, то А = С.
Шкалы порядка (рангов)являются монотонно изменяющимися и позволяют установить отношение «больше – меньше» между величинами, характеризующими это свойство. Если для обозначения реперных точек используются цифры, то они называются баллами.
Обозначения нельзя ни складывать, ни вычитать, ни делить, ни перемножать, т.е. на шкале порядка не определены никакие математические операции.
В то же время, если один размер по шкале порядка меньше другого, а последний в свою очередь меньше третьего, то и первый размер меньше третьего. Т.е. для любых чисел a, b и c таких, что a < b и b < c , справедливо соотношение a < c (транзитивность). Эти свойства транзитивностиозначают, что на шкалах порядка определены (т.е. могут выполняться) логические операции. По шкалам порядка не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. В шкалах порядка принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности. Хотя нуль может и существовать.
Тем не менее, в областях, где к измерительной информации не предъявляются высокие требования, шкалы порядка применяются довольно широко.
Пример - В образовательных учреждениях по шкале порядка, представленной в таблице 1.4, измеряются знания учащихся.
Таблица 1.4 – Сравнение российской и международной систем оценки знаний
| Российские оценки | ECTS | Смысловое содержание оценки |
| 5 | A | Отлично |
| 4 | B | Очень хорошо |
| C | Хорошо | |
| 3 | D | Удовлетворительно |
| E | Посредственно | |
| 2 | FX | Неудовлетворительно (с правом пересдачи) |
| * | F | Неудовлетворительно (без права пересдачи) |
При одномерной шкале порядок должен быть линейным: все объекты должны поддаваться выстраиванию в цепочку по какому-либо признаку (некоторые из них могут занять одно и то же место в цепочке – быть эквивалентными). Так, студенты после экзамена разбиваются на классы получивших оценки 2, 3, 4 и 5 в порядке роста их знаний, но для экзаменатора и внутри этих классов есть различия. Здесь существенно, что более знающему студенту присваивается большее число, и переставлять эти числа уже нельзя. Правда, можно договориться о другом порядке оценок, но это изменит всю систему. Так, суждения о студентах не изменились бы, если бы вместо оценок 2, 3, 4 и 5 ставились 5, 10, 15 и 20 (мог бы измениться средний балл, но это потому, что средний балл является так называемой неадекватной статистикой для шкалы порядка).
Группа допустимых преобразований для шкалы порядка должна уничтожать пропорциональность (ведь знания, оцененные на 4, нельзя считать вдвое более обширными или глубокими, чем знания, оцененные на 2 и отношение «быть суммой» (получить 2 и 3 – не то же, что получить 5), сохраняя лишь отношения большего и меньшего.
Упорядочение в шкале порядка может осуществляться по внешним признакам (нумерация) или по внутренним свойствам (ранжирование).
Примеры:
- нумерация мест в театрах, домов на улице, исследуемых образцов промышленных изделий и т.д.;
- ранжирование силы ветра (волнения) на море (12-балльная шкала Бофорта для силы морского ветра), ранжирование силы землетрясений (шкала Рихтера), шкала вязкости Энглера.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам относится шкала Мооса для определения твердости минералов, представленная в таблице 1.5. В ней определенным стандартным минералам от талька до алмаза в порядке возрастания их твердости присвоены целые числа от 1 до 10.
Таблица 1.5 - Минералогическая шкала твёрдости
| Балл | Твёрдость |
| Меньше твёрдости талька | |
| Равна или больше твёрдости талька, но меньше твёрдости гипса | |
| Равна или больше твёрдости гипса, но меньше твёрдости извес ткового шпата | |
| Равна или больше твёрдости известкового шпата, но меньше твёрдости плавикового шпата | |
| Равна или больше твёрдости плавикового шпата, но меньше твёрдости апатита | |
| Равна или больше твёрдости апатита, но меньше твёрдости полевого шпата | |
| Равна или больше твёрдости полевого шпата, но меньше твёрдости кварца | |
| Равна или больше твёрдости кварца, но меньше твёрдости топаза | |
| Равна или больше твёрдости топаза, но меньше твёрдости корунда | |
| Равна или больше твёрдости корунда, но меньше твёрдости алмаза | |
| Равна твёрдости алмаза или больше её |
Определение значений величин с помощью шкал порядка нельзя считать измерениями, так как на них отсутствуют единицы измерения.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным. Не все объекты можно подчинить отношению порядка. Например, нельзя сказать, что больше - круг или треугольник, но можно выделить в этих объектах общее свойство - площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы.
3-net.ru
Метрические шкалы
Количество просмотров публикации Метрические шкалы - 1366
Порядковые шкалы
Номинативные шкалы
Виды психодиагностических шкал
Измерительные шкалы(от лат. scala – ʼʼлестницаʼʼ) – форма фиксации совокупности признаков изучаемого объекта с упорядочиванием их в определенную числовую систему. Наиболее общая классификация измерительных шкал предложена С. Стивенсон. В ее основу положен признак метрической детерминированности. Согласно этому признаку шкалы делятся на метрические(интервальные и шкалы отношений) и неметрические(номинативные, шкалы порядка).
Номинативные шкалы (шкалы наименований)устанавливают соответствие признака тому или иному классу. Объекты объединяют в классы на основании какого-либо общего свойства (классы эквивалентности) либо символа (обозначения). Необязательно, чтобы между выявленными классами существовала внутренняя взаимосвязь. Само название ʼʼшкала наименованийʼʼ указывает на то, что значения по шкале играют роль лишь названий классов. Одним из распространенных видов номинативной шкалы является классификация объектов на две группы по принципу ʼʼА – не-Аʼʼ (альтернативные признаки в дихотомической шкале наименований). Конкретными примерами применения такой шкалы являются оценивание ответа испытуемого на пункт опросника в виде утверждения или отрицания, соответствие или несоответствие полученного вида ответа ключу (коду) измеряемого свойства (см. личностные опросники).
Примером оценивания в номинативной шкале могут служить классификация решений тестовой задачи или пункт опросника с задачей закрытого типа.
В строгом смысле номинативная шкала не является шкалой измерения. Она допускает лишь операцию равенства и неравенства и более или менее дифференцированную классификацию признаков. Вместе с тем в психологических исследованиях и психологической диагностике данный вид измерительных шкал имеет достаточно большое значение, особенно при фиксации качественной информации (к примеру, данных проективных методик при сборе психологического анамнеза и т. д.).
Порядковые шкалы (ординальные)предназначены для расчленения совокупности признаков на элементы, связанные отношением ʼʼбольше – меньшеʼʼ, и допускают отнесение переменных к группам, упорядоченным (ранжированным) друг относительно друга и представляющим некое системное единство. Порядковые шкалы дают возможность оценить степень выраженности признака. Οʜᴎ содержат не менее трех классов с установленной последовательностью, не допускающей перестановки. Упорядочивание признаков в ординальной шкале должна быть униполярным (при определении классов исходят из степени выраженности измеряемого свойства) и биполярным (в базе разделения лежит ранг степени приближения к одному из противоположных полюсов свойства).
В качестве примера униполярного упорядочивания должна быть приведена шкала оценивания качеств внимания: ʼʼвесьма устойчивое /устойчивое / лабильное / рассеянноеʼʼ. Примером оценивания по биполярному принципу может служить идентификация выраженности свойств между полярными антонимическими характеристиками свойств личностных проявлений:
1) уравновешенный… нестабильный;2) общительный… замкнутый;3) подвижный… медлительный.
Порядковые шкалы относятся к числу распространенных в психологической диагностике
Шкала интервалов относится к метрическим шкалам, в которых элементы упорядочены не только по принципу выраженности измеряемого признака, но и на базе ранжирования признаков по размеру, что выражается интервалами между числами, приписываемыми степени выраженности измеряемого признака.
В шкале интервалов нулевая точка отсчета может устанавливаться произвольно, а величины единиц и направление отсчета могут определяться по избираемым константам.
К разряду шкалы интервалов относятся шкалы стандартного IQ-показателя, Т-баллов, процентилей и другие (см. стандартизация, оценки шкальные). Шкалирование в интервальной шкале составляет основу психометрических измерений.
В шкалах отношений (пропорциональных) числовые значения присваиваются объектам таким образом, чтобы между числами и объектами соблюдалась пропорциональность. Начало отсчета в такой шкале фиксировано. Шкала предусматривает операции равенства / неравенства, больше / меньше, равенства интервалов и равенства отношений.
Примером использования такой шкалы в психологических измерениях может служить шкала порогов абсолютной чувствительности анализатора.
Наряду с делением шкал на метрические и неметрические существует классификация по признаку формы фиксации эмпирических данных, а именно: шкалы вербальные, шкалы числовые и шкалы графические.
Читайте также
Основные типы шкал Понятие шкалы измерений. Основные типы шкал измерений Лекция №5. Шкалы измерений Многообразные проявления конкретного свойства объекта измерения образуют множество, элементы которого находятся в определенных... [читать подробнее].
Основные типы шкал Понятие шкалы измерений. Основные типы шкал измерений Лекция №5. Шкалы измерений Многообразные проявления конкретного свойства объекта измерения образуют множество, элементы которого находятся в определенных... [читать подробнее].
Шкала разностей описывает свойство, для которого имеют смысл не только отношения эквивалентности и порядка, но и отношения аддитивности – суммирования интервалов (разностей между различными количественными проявлениями свойства). Шкала разностей имеет условную... [читать подробнее].
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению... [читать подробнее].
Измерительные шкалы 1.4.1 Шкала физической величины Шкала физической величины (от латин. scala - лестница ) представляет собой упорядоченную совокупность значений этой величины, служащую исходной основой для измерений данной величины, принятую по соглашению... [читать подробнее].
Шкалы интервалов (разностей) являются дальнейшим развитием шкал порядка и относятся уже к метрическим шкалам. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. На шкалах интервалов по сравнению с... [читать подробнее].
Качество ПО - это совокупность свойств, определяющих полезность изделия (программы) для пользователей в соответствии с функциональным назначением и предъявлёнными требованиями. Характеристика качества программы - понятие, отражающее отдельные факторы, влияющие на... [читать подробнее].
referatwork.ru
Шкалы измерений в метрологии | Виды шкал: номинальные, абсолютные, порядка, отношений, интервалов
Шкала измерений – это совокупность значений, позволяющих количественно или качественно отобразить свойства объекта измерений. Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины - это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.
Виды шкал измерений
В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства измерительных шкал в метрологии проявляются только качественно, другие - количественно.
Шкала – упорядоченный числовой или символьный ряд значений, отражающий допустимые вариации значений измеряемой величины.
В соответствии с логической структурой проявления свойств различают пять основных видов шкал измерений: шкалы наименований, шкалы порядка, шкалы интервалов, шкалы отношений, абсолютные шкалы.
Номинальная шкала (шкала наименований)
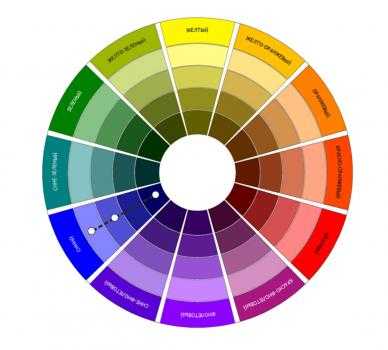
Рисунок – Пример номинальной шкалы (атлас цветов)
Такие шкалы измерений в метрологии используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида но являются шкалами ФВ. Номинальные шкалы, или, как их еще называют шкалы наименований так же называют шкалами измерений, или шкалами классификаций. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.
В номинальных шкалах, в которых отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. При этом большое значение имеет правильный выбор классов эквивалентной шкалы - они должны надежно различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: "не приписывай одну и ту же цифру разным объектам". Числа, приписанные объектам, могут быть использованы для определения вероятности или частоты появления данного объекта, но их нельзя использовать для суммирования и других математических операций.
Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствует понятия нуля, "больше" или "меньше" и единицы измерения. Примером номинальных шкал являются широко распространенные атласы цветов, предназначенные для идентификации цвета.
Шкала порядка (рангов)
Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала - это шкала ФВ, исходные значения которой выражены в условных единицах. Пример шкалы порядка - шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.
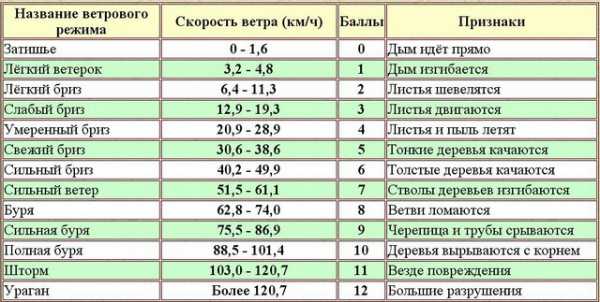
Рисунок - Пример шкалы порядка (шкала Бофорта)
Широкое распространение получили шкалы измерений порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) - не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,
В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операция. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
Шкала интервалов (разностей)
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов - летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
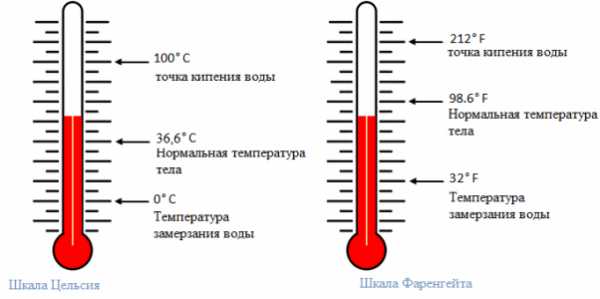
Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
Шкала интервалов величины Q описывается уравнением Q = Qо + q[Q], где q - числовое значение величины; Qо - начало отсчета шкалы; [Q] - единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины [Q].
Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) - основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n=[Qо] за единицу Q. При этом n выбирается таким, чтобы [Q] было целой величиной.

Рисунок – Пример шкалы отношений
При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода - шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
Шкала отношений
Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода - аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода - пропорциональные). Пример шкалы отношений - шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин.
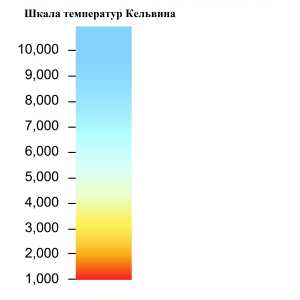
Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)
Шкалы отношений - самые совершенные. Они описываются уравнением Q = q[Q], где Q - ФВ, для которой строится шкала, [Q] - ее единица измерения, q - числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1[Q1]/[Q2].
Абсолютные шкалы
Абсолютные шкалы - это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений - метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Изготовление измерительной шкалы своими руками
Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.
Похожие материалы
www.metalcutting.ru
Типы измерительных шкал
А) Этническая принадлежность (номинальная шкала). Три боксера (братья Кличко и Димитренко) являются украинцами, один (Поветкин) - русским, один (Адамек) - Поляком, два (Чемберс и Томпсон) - американцами, один (Фьюри) - британцем, один (Хелениус) - фином, один (Пулев) - болгарином. Таким образом переменная "национальность" помогла нам разделить всех боксеров на 7 групп, в зависимости от их этнической принадлежности. Владея этими данными, человек далекий от бокса ничего не сможет сказать об успешности перечисленных боксеров, хотя и получит информацию об этнической принадлежности 10-ти наилучших тяжеловесов (мы и далее будет обращаться к гипотетическому эксперту): украинцы - 30%; американцы - 20%; русские, поляки, британцы, фины и болгары - по 10%. Б) Место в рейтинге (порядковая шкала) дает приблизительную информацию об успешности боксера. Ситуация следующая: 1. Владимир Кличко 2. Виталий Кличко 3. Александр Поветкин 4. Томаш Адамек 5. Эдди Чемберс 6. Тайсон Фьюри 7. Роберт Хелениус 8. Тони Томпсон 9. Александр Димитренко 10. Кубрат Пулев Теперь наш неосведомленный аналитик знает последовательность первой десятки боксеров супертяжелого веса. И хотя здесь уже присутствуют числа от 1 до 10, он все еще не может осуществлять никаких математических операций кроме сравнения. К примеру, он не может сказать, что Владимир Кличко лучше Эдди Чемберса на 4 единицы. Выражение "5 минус 1" в данном случае не имеет смысла. В отношении этих двух боксеров он может утверждать лишь то, что Владимир Кличко лучше Эдди Чемберса как боксер (как впрочем и всех остальных из десятки). Причина невозможности осуществления математических действий заключается в том, что между пунктами с 1-го по 10-й нет равенства интервалов. Каковы на самом деле интервалы между пунктами, можно увидеть благодаря последней переменной. В) Количество рейтинговых очков (метрическая шкала). Данный показатель высчитывается с помощью специальной формулы, в основе которой лежит рейтинг противников, а также результаты соответствующих поединков (нокаут, технический нокаут, победа единогласным решением и т.д.). В результате измерение успешности боксеров носит намного более точный характер, чем в случае простого места в рейтинге. Соответствующие очки приведены ниже:Место в рейтинге | Боксер | Количество рейтинговых очков |
1 | Владимир Кличко | 1331 |
2 | Виталий Кличко | 1213 |
3 | Александр Поветкин | 519 |
4 | Томаш Адамек | 452 |
5 | Эдди Чемберс | 450 |
6 | Тайсон Фьюри | 442 |
7 | Роберт Хелениус | 430 |
8 | Тони Томпсон | 420 |
9 | Александр Димитренко | 413 |
10 | Кубрат Пулев | 396 |
soc-research.info
Видеоматериалы
Опыт пилотных регионов, где соцнормы на электроэнергию уже введены, показывает: граждане платить стали меньше
Подробнее...С начала года из ветхого и аварийного жилья в республике были переселены десятки семей
Подробнее...Более 10-ти миллионов рублей направлено на капитальный ремонт многоквартирных домов в Лескенском районе
Подробнее...Актуальные темы
ОТЧЕТ о деятельности министерства энергетики, ЖКХ и тарифной политики Кабардино-Балкарской Республики в сфере государственного регулирования и контроля цен и тарифов в 2012 году и об основных задачах на 2013 год
Подробнее...Предложения организаций, осуществляющих регулируемую деятельность о размере подлежащих государственному регулированию цен (тарифов) на 2013 год
Подробнее...
КОНТАКТЫ
360051, КБР, г. Нальчик
ул. Горького, 4
тел: 8 (8662) 40-93-82
факс: 8 (8662) 47-31-81
e-mail:
Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.