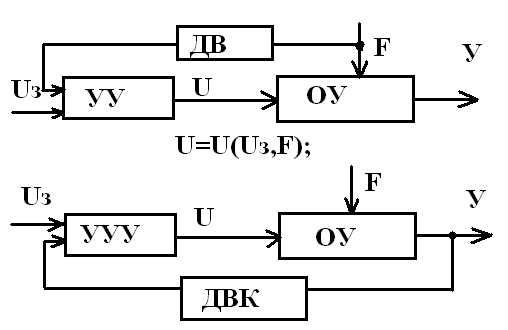
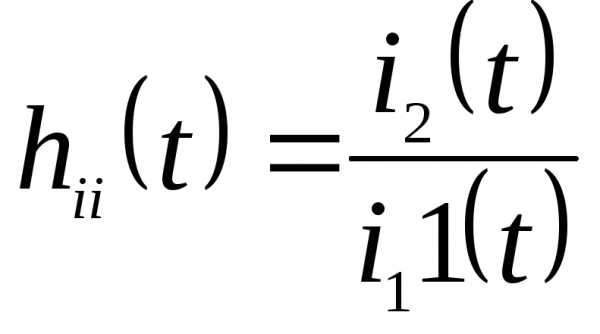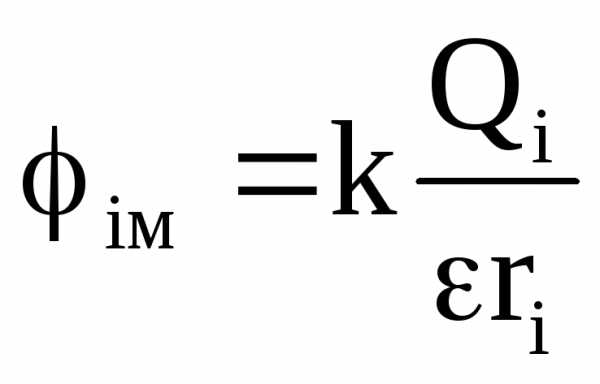Параллельное соединение сопротивлений. Общее сопротивление резисторов при параллельном соединении

Сопротивление при параллельном соединении: формула расчета. При параллельном соединении мощность

Последовательное и параллельное подключение

Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.

Основные принципы

Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.

Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.

Параллельное подключение

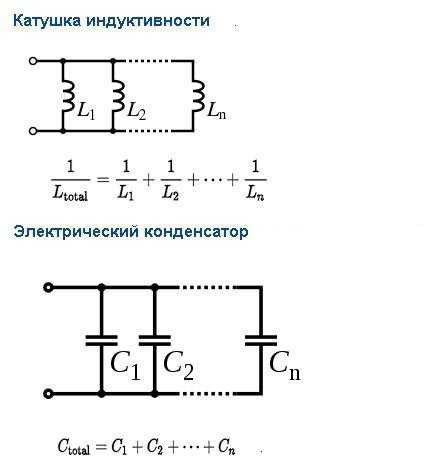
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.

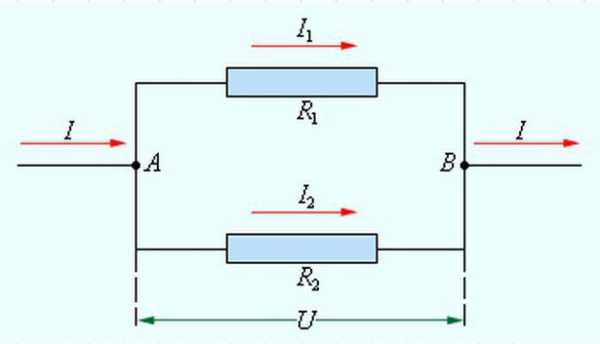
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым – во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.

При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.

Последовательное подключение

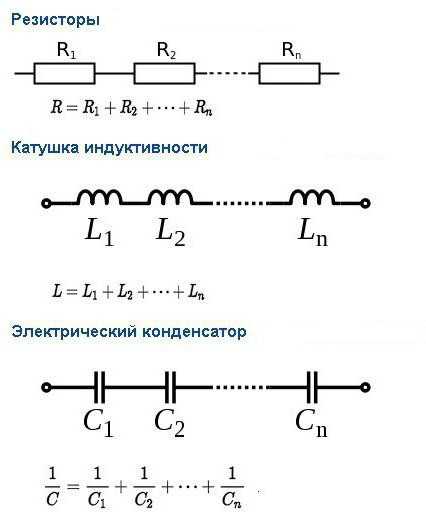
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.

Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.

В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.

Смешанные схемы

Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.

Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.

Подключение светодиодов

Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. Схема подключения светодиодов во многом зависит от напряжения источника тока.

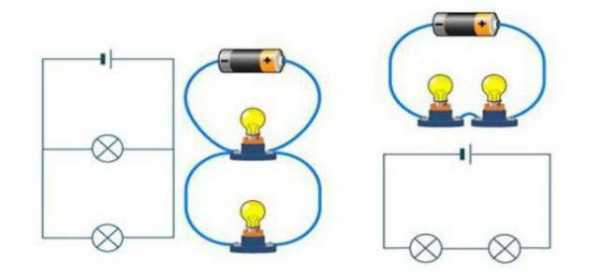
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.

При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.

Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй – после.

При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.

fb.ru

Параллельное соединение резисторов

Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.

Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье.  Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .

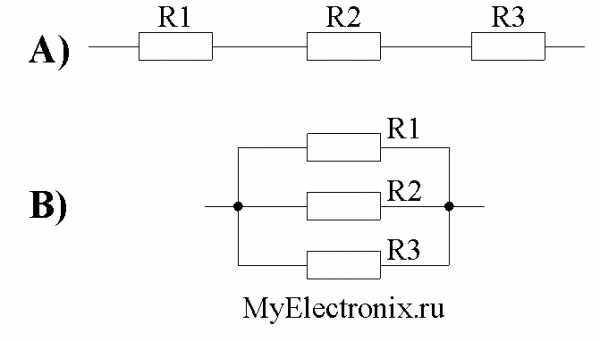
А) – Последовательное соединение

В) – Параллельное соединение

Рисунок 1 – Последовательное и параллельное соединение

Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.

Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.

 

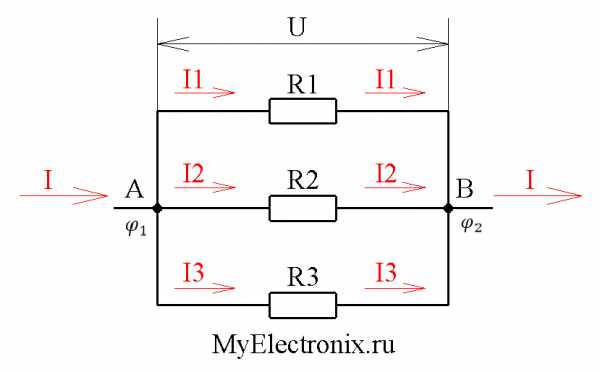
Рисунок 2 – Параллельное соединения

Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.

Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.

С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство

То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.

Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вно

xn----7sbeb3bupph.xn--p1ai

Последовательное и параллельное соединение сопротивлений

Последовательное соединение сопротивлений

Возьмем три неизменных сопротивления R1, R2 и R3 и включим их в цепь так, чтоб конец первого сопротивления R1 был соединен с началом второго сопротивления R2, конец второго — с началом третьего R3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1).

Такое соединение сопротивлений именуется поочередным. Разумеется, что ток в таковой цепи будет во всех ее точках один и тот же.

Рис 1. Последовательное соединение сопротивлений

Как найти общее сопротивление цепи, если все включенные в нее поочередно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:

U = U1 + U2 + U3

где

U1 = IR1 U2 = IR2 и U3 = IR3

либо

IR = IR1 + IR2 + IR3

Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3).

Поделив сейчас обе части равенства на I, будем совсем иметь R = R1 + R2 + R3

Таким макаром, мы сделали вывод, что при поочередном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Проверим этот вывод на последующем примере. Возьмем три неизменных сопротивления, величины которых известны (к примеру, R1 == 10 Ом, R2 = 20 Ом и R3 = 50 Ом). Соединим их поочередно (рис. 2) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).

Рис. 2. Пример поочередного соединения 3-х сопротивлений

Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим наружное сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.

Найдем ток в цепи по закону Ома: 60 / 80= 0,75 А

Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U1 = 0,75х 10 = 7,5 В, U2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.

Зная падение напряжений на участках, определим общее падение напряжения во наружной цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.

Мы получили таким макаром, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Разъясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.

Замкнув сейчас ключ выключатель К, можно убедиться по устройствам, что наши подсчеты приблизительно верны.

Параллельное соединение сопротивлений

Возьмем два неизменных сопротивления R1 и R2 и соединим их так, чтоб начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив потом точки а и б с источником тока, получим замкнутую электронную цепь. Такое соединение сопротивлений именуется параллельным соединением.

Рис 3. Параллельное соединение сопротивлений

Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, потому что тут сама цепь разветвляется на две отдельные ветки: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I2. Любой из этих токов пойдет по собственной ветки до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.

Таким макаром, при параллельном соединении сопротивлений выходит разветвленная цепь. Поглядим, какое же будет соотношение меж токами в составленной нами цепи.

Включим амперметр меж положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив потом амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.

Означает, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).

Будем сейчас включать амперметр попеременно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветки амперметр покажет силу тока I1, а во 2-ой — I2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).

Как следует, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки.I = I1 + I2 Выражая это формулой, получим

Это соотношение, имеющее огромное практическое значение, носит заглавие закона разветвленной цепи.

Разглядим сейчас, каково будет соотношение меж токами в ветвях.

Включим меж точками а и б вольтметр и поглядим, что он нам покажет. Во-1-х, вольтметр покажет напряжение источника тока, потому что он подключен, как это видно из рис. 3, конкретно к зажимам источника тока. Во-2-х, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, потому что он соединен с началом и концом каждого сопротивления.

Как следует, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.

Это дает нам право написать, что U = U1 = U2,

где U — напряжение на зажимах источника тока; U1 — падение напряжения на сопротивлении R1, U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR.

Потому для каждой ветки можно написать: U1 = I1R1 и U2 = I2R2, но потому что U1 = U2, то и I1R1 = I2R2.

Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветки будет во столько раз больше (либо меньше) тока во 2-ой ветки, во сколько раз сопротивление первой ветки меньше (либо больше) сопротивления 2-ой ветки.

Итак, мы пришли к принципиальному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, назад пропорциональные величинам сопротивлении параллельных веток. По другому говоря, чем больше сопротивление ветки, тем наименьший ток потечет через нее, и, напротив, чем меньше сопротивление ветки, тем больший ток потечет через эту ветвь.

Убедимся в корректности этой зависимости на последующем примере. Соберем схему, состоящую из 2-ух параллельно соединенных сопротивлений R1 и R2, присоединенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.

Подсчитаем поначалу, что покажет нам амперметр, включенный в каждую ветвь:

I1 = U / R1 = 3 / 10 = 0,3 А = 300 мА

I2 = U / R2 = 3 / 20 = 0,15 А = 150 мА

Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА

Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется назад пропорционально сопротивлениям.

Вправду, R1 == 10 Ом в два раза меньше R2 = 20 Ом, при всем этом I1 = 300 мА в два раза больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через наименьшее сопротивление (R1 = 10 Ом), а наименьшая часть (R2 = 150 мА) —через большее сопротивление (R2 = 20 Ом).

Такое разветвление тока в параллельных ветвях сходно с течением воды по трубам. Представьте для себя трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного поперечника (рис. 4). Потому что поперечник трубы Б больше поперечника трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает сгустку воды большее сопротивление.

Рис. 4. Через узкую трубу в один и тот же просвет времени пройдет воды меньше, чем через толстую

Разглядим сейчас, чему будет равно общее сопротивление наружной цепи, состоящей из 2-ух параллельно соединенных сопротивлений.

Под этим общим сопротивлением наружной цепи нужно осознавать такое сопротивление, которым можно было бы поменять при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при всем этом тока до разветвления. Такое сопротивление именуется эквивалентным сопротивлением.

Вернемся к цепи, показанной на рис. 3, и поглядим, чему будет равно эквивалентное сопротивление 2-ух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R, где I — ток во наружной цепи (до точки разветвления), U — напряжение наружной цепи, R — сопротивление наружной цепи, т. е. эквивалентное сопротивление.

Точно так же для каждой ветки I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления веток.

По закону разветвленной цепи: I = I1 + I2

Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2

Потому что при параллельном соединении U = U1 = U2, то можем написать U / R = U / R1 + U / R2

Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2)

Разделив сейчас обе части равенства на U, будем совсем иметь 1 / R= 1 / R1 + 1 / R2

Помня, что проводимостью именуется величина, оборотная сопротивлению, мы можем сказать, что в приобретенной формуле 1 / R — проводимость наружной цепи; 1 / R1 проводимость первой ветки; 1 / R2- проводимость 2-ой ветки.

На основании этой формулы делаем вывод: при параллельном соединении проводимость наружной цепи равна сумме проводимостей отдельных веток.

Как следует, чтоб найти эквивалентное сопротивление включенных параллельно сопротивлений, нужно найти проводимость цепи и взять величину, ей оборотную.

Из формулы также следует, что проводимость цепи больше проводимости каждой ветки, а это означает, что эквивалентное сопротивление наружной цепи меньше меньшего из включенных параллельно сопротивлений.

Рассматривая случай параллельного соединения сопротивлений, мы взяли более ординарную цепь, состоящую из 2-ух веток. Но на практике могут повстречаться случаи, когда цепь состоит из 3-х и поболее параллельных веток. Как поступать в этих случаях?

Оказывается, все приобретенные нами соотношения остаются справедливыми и для цепи, состоящей из хоть какого числа параллельно соединенных сопротивлений.

Чтоб убедиться в этом, разглядим последующий пример.

Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5).

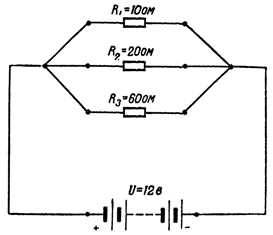
Рис. 5. Цепь с 3-мя параллельно соединенными сопротивлениями

Применяя для этой цепи формулу 1 / R= 1 / R1 + 1 / R2, можем написать 1 / R= 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R= 1 / 10 + 1 / 20 + 1 / 60

Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Как следует, эквивалентное сопротивление R = 6 Ом.

Таким макаром, эквивалентное сопротивление меньше меньшего из включенных параллельно в цепь сопротивлений, т. е. меньше сопротивления R1.

Поглядим сейчас, вправду ли это сопротивление является эквивалентным, т. е. таким, которое могло бы поменять включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при всем этом силы тока до разветвления цепи.

Допустим, что напряжение наружной цепи, а как следует, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1,2 А I2 = U/R2 = 12 / 20 = 1,6 А I3 = U/R1 = 12 / 60 = 0,2 А

Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.

Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если заместо 3-х параллельно включенных узнаваемых нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.

I = U/R= 12 / 6 = 2 А

Как лицезреем, отысканное нами сопротивление R = 6 Ом вправду является для данной цепи эквивалентным.

В этом можно убедиться и на измерительных устройствах, если собрать схему с взятыми нами сопротивлениями, измерить ток во наружной цепи (до разветвления), потом поменять параллельно включенные сопротивления одним сопротивлением 6 Ом и опять измерить ток. Показания амперметра и в том и в другом случае будут приблизительно схожими.

На практике могут повстречаться также параллельные соединения, для которых высчитать эквивалентное сопротивление можно проще, т. е. не определяя за ранее проводимостей, сходу отыскать сопротивление.

К примеру, если соединены параллельно два сопротивления R1 и R2, то формулу 1 / R= 1 / R1 + 1 / R2 можно конвертировать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2), т. е. при параллельном соединении 2-ух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.

elektrica.info

Параллельное соединение сопротивлений | Техника и Программы

Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму – концы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Общее сопротивление параллельно включенных сопротивлений определяется по формуле

 

 

 

 Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение.

На вышеуказанном рисунке мы можем сразу сказать что общее сопротивление будет меньше 10 ом.

Первый частный случай

Если параллельно включено только два резистора  то их общее сопротивление можно определить по формуле

 

 

 

 

 

 

 

 

 

 

 

 

 

 Так как начала всех сопротивлений сведены в одну общую точку, а концы – в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.

Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.

 

 

 

 Если разветвление подключено непосредственно к зажимам источника тока, то напряжение на каждом из сопротивлений равно напряжению на зажимах источника.

 

 

 Второе свойство цепи с параллельным соединением  заключается в том, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.

Это значит что чем больше сопротивление тем меньше по нему пойдет ток.

 

 

 

 Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:

 

 

 Следовательно, третье свойство параллельного соединения может сформулирована так:

Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.

nauchebe.net

Параллельное соединение резисторов

Физика > Параллельное соединение резисторов

 

В параллельной цепи полное сопротивление достигает суммы инверсии каждого.

Задача обучения

• Определить общее сопротивление.

Основные пункты

• В параллельном соединении полное сопротивление меньше, чем наименьшее из отдельных.
• Каждый резистор наделен одним напряжением.
• Параллельные резисторы получают общее количество тока, но и делят его.

Термины

• Параллельность – расположение электрических составляющих так, чтобы ток протекал вдоль двух или более путей.
• Сопротивление – противодействие потоку электрического тока.

Обзор

Резисторы в цепи могут располагаться последовательно или параллельно. Полное сопротивление зависит от индивидуальных значений и метода связи.

Параллельное соединение

Мы сталкиваемся с параллельным соединением, если каждый резистор подключается к источнику напряжения индивидуально. Поэтому каждый обладает полным напряжением.

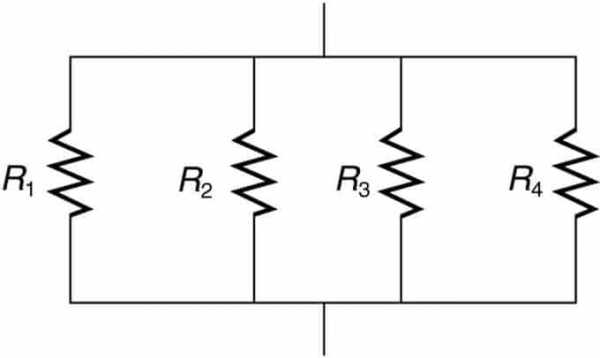
Параллельное соединение резисторов

Резисторы используют столько тока, как если бы они были единственными в цепи. Это применяют в доме, чтобы обеспечить независимую работу прибора.

Закон Ома в параллельном подключении

У каждого резистора есть полное напряжение. Тогда закон Ома будет выглядеть как:

I1 = V/R1

I2 = V/R2

I3 = V/R3.

Суммарный ток будет приравниваться к результату сложения отдельных:

Три резистора в параллельном соединении с батареей и эквивалентным сопротивлением

I = I1 + I2 + I3.

Подставим выражение для отдельных токов: I = V/R1 + V/R2 + V/R3 или I = V (1/R1 + 1/R2 + 1/R3).

Мы видим, что общее сопротивление в параллельном подключении достигает суммы инверсии каждого отдельного. Поэтому выходим на формулу:

Rn(параллельно) = 1/R1 + 1/R2 + 1/R3 ... + 1/Rn.

Подобное соотношение выводит на суммарное сопротивление, которое уступает наименьшему из индивидуальных. При параллельном подключении больше тока протекает от источника, чем поток для каждого по отдельности, поэтому сопротивление ниже.

Каждый резистор обладает полным напряжением источника, но и разделяют общий ток. Например, у нас есть батарея 1.5В. В последовательном подключении две лампочки будут гореть также ярко, как если бы это была всего одна. Однако батарея расходуется быстрее, потому что гарантирует полную энергию сразу для двух лампочек.

v-kosmose.com

---

• 
  Индукцией навыков
• 
  Пушкинская электросеть
• 
  Генератор для света
• 
  Классификация сау
• 
  Отключили электричество куда звонить
• 
  Переходные процессы в линейных электрических цепях
• 
  Количество протонов электронов и нейтронов в атоме
• 
  По какой формуле вычисляется емкость плоского конденсатора
• 
  Муфта электромагнитная сцепления
• 
  Пропан сжиженный газ это
• 
  Сколько населения в ставрополе 2018