Опыты Фарадея — Магнитное поле. Закон электромагнитной индукции
I. Опыты Фарадея
Английский физик Майкл Фарадей, узнав об опытах Эрстеда, занялся
поисками связи магнитных явлений с электрическими. Он поставил перед
собой задачу: «Если электрический ток создает магнитное поле, то нельзя
ли с помощью магнитного поля получить электрический ток?» Поиски Фарадея
продолжались с 1821 до 1831 года. Он провел значительную работу и
проявил находчивость, настойчивость и упорство, пока, наконец, не
получил электрический ток с помощью магнитного поля. Фарадей доказал,
что магнитное поле может порождать электрический ток, открыв явление
электромагнитной индукции. На этом явлении основана сегодня действие
генераторов электрического тока на всех электростанциях Земли.
Можно провести ряд опытов, которые являются современными вариантами опытов Фарадея.
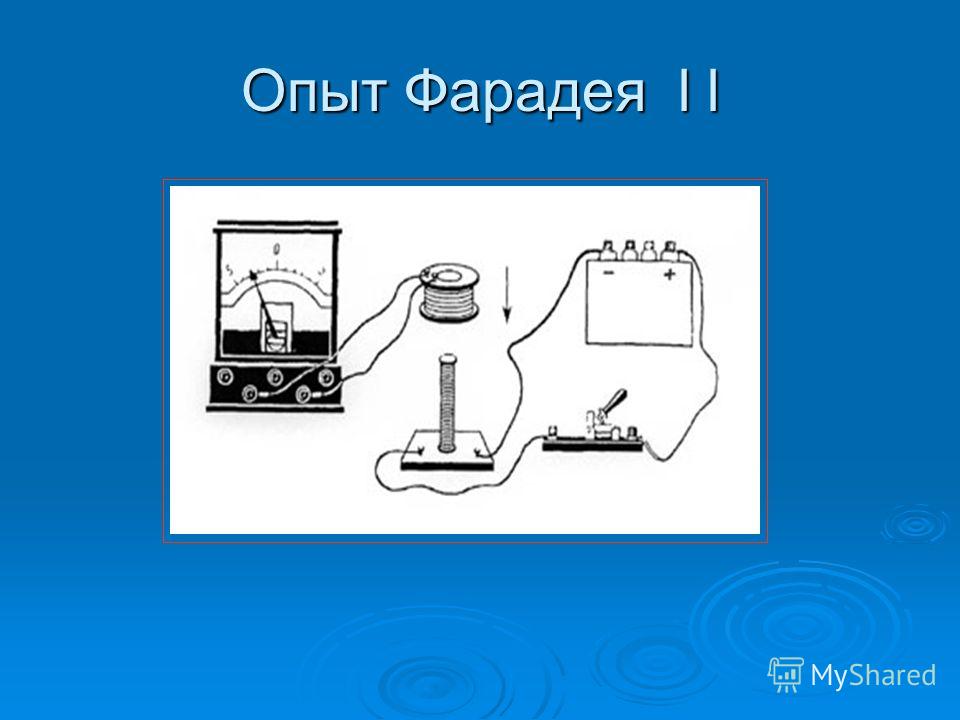
Опыт 1. Замыкаем катушку на гальванометр и вводим в нее постоянный
магнит. Во время движения магнита стрелка гальванометра отклоняется, что
свидетельствует о наличии электрического тока.
Если оставить магнит неподвижным, а двигать катушку, то электрический ток в катушке возникает только во время ее движения.
Опыт 2. Если взять две катушки и надеть их на общий сердечник, то в
случае изменения силы тока в одной катушке в другой катушке можно
наблюдать появление тока.
Опыт 3. Если вращать замкнутую катушку вблизи полюса магнита, то в катушке возникает электрический ток.
Опыт 4. Если разместить вблизи полюса магнита замкнутый контур и изменять его площадь, то в контуре возникает электрический ток.
Просмотрите опыты Фарадея. Для этого
1. Установите программу на свой ПК.(смотри ниже)
2. Чтобы данный симулятор открылся успешно, Вам необходимо загрузить и установить Java и Adobe Flash Player
В программе представлены опыты:
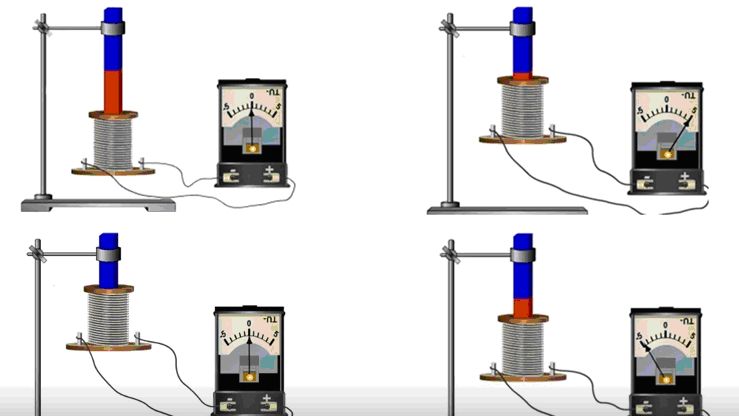
1. Постоянный магнит и действие магнита на компас.
Отображаются магнитные линии, регулируется сила магнита, показывается магнитное поле.
2. Катушка и постоянный магнит.
Катушка и постоянный магнит.
Регулируется количество витков катушки и площадь витка. Отображается движение электронов в катушке. Два вида индикаторов.
3. Электромагнит и его действие на компас.
Два вида источника тока- источники постоянного и переменного тока. Регулируется количество витков катушки.
4. Трансформатор.
Приёмная катушка (2 видами индикаторов) + электромагнит (источники постоянного и переменного тока).
Поток магнитной индукции
Проанализировав перечисленные выше опыты, можно заметить, что в
замкнутом проводящем контуре ток возникает лишь тогда, когда меняется
число линий магнитной индукции, пронизывающих поверхность, ограниченную
контуром. Физическую величину, которую наглядно можно рассмотреть как
величину, пропорциональную числу линий магнитной индукции, пронизывающих
эту поверхность, называют потоком магнитной индукции (или магнитным
потоком).
Ø Поток магнитной индукции Ф — это физическая величина,
характеризующая распределение магнитного поля по поверхности,
ограниченной замкнутым контуром, и численно равна произведению магнитной
индукции B на площадь S поверхности и на косинус угла а между вектором магнитной индукции и нормалью к поверхности:
Ф = BScos.
Единица потока магнитной индукции в СИ — вебер:
1 Вб = 1 Тл · м2.
Магнитный поток 1 Вб создает однородное магнитное поле с индукцией 1
Тл через поверхность площадью 1 м2, расположенную перпендикулярно
вектору магнитной индукции.
Исходя из формулы Ф = BScos, все опыты можно условно разделить на три группы:
а) опыты, в которых изменяется индукция магнитного поля B;
б) опыты, в которых изменяется площадь контура S;
в) опыты, в которых изменяется угол между направлением вектора магнитной индукции и нормалью к площадке.
На основании выполненных исследований можно подвести учащихся к
выводу: для возбуждения электрического тока в замкнутом контуре
необходимо изменять магнитный поток через этот контур.
Явление электромагнитной индукции заключается вот в чем:
Ø индукционный ток в замкнутом контуре возникает при изменении магнитного потока через площадь, ограниченную контуром.
Существуют две причины возникновения индукционного тока:
1) во время движения контура в магнитном поле;
2) во время нахождения недвижимого контура в переменном магнитном поле.
Опыты Фарадея (электромагнитная индукция)
Электромагнитная индукция
В начале XIX столетия опыты в области электромагнетизма стали чуть ли не модой. Открытие в 1820 г. Эрстедом существование магнитного поля вокруг проводника с током вызвало небывалый резонанс в научных кругах. Проводилось множество экспериментов с электричеством.
29 августа 1831 г. Фарадеем эмпирически было открыто явление электромагнитной индукции. Первоначально данное явление Фарадей обнаружил для стационарных по отношению друг к другу проводников при замыкании и размыкании цепи. Чуть позднее ученый показал, что явление электромагнитной индукции обнаруживается при движении катушек с токами друг по отношению к другу. 17 октября Фарадей отметил в лабораторном журнале, что обнаружил индукционный ток во время введения и удаления магнита в (из) катушку. За один месяц Фарадей определил все основные особенности явления электромагнитной индукции.
Опыты Фарадея
В настоящее время классическими опытами Фарадея по обнаружению явления электромагнитной индукции являются следующие эксперименты:
- Гальванометр замыкают на соленоид.
 В соленоид вдвигается (или выдвигается из него) постоянный магнит. При перемещении магнита фиксируют отклонение стрелки гальванометра, что означает возникновение индукционного тока. При увеличении скорости перемещения магнита по отношению к катушке отклонение стрелки увеличивается. Замена полюсов магнита вызывает изменение направления отклонения стрелки гальванометра. Отметим, что магнит можно оставить неподвижным и перемещать соленоид относительно магнита.
В соленоид вдвигается (или выдвигается из него) постоянный магнит. При перемещении магнита фиксируют отклонение стрелки гальванометра, что означает возникновение индукционного тока. При увеличении скорости перемещения магнита по отношению к катушке отклонение стрелки увеличивается. Замена полюсов магнита вызывает изменение направления отклонения стрелки гальванометра. Отметим, что магнит можно оставить неподвижным и перемещать соленоид относительно магнита. - В этом эксперименте используются две катушки. Одна вставлена в другую. Концы одной из катушек соединяют с гальванометром. Через другую катушку пропускается электрический ток. Стрелка гальванометра претерпевает отклонения, когда происходит включение (выключение) тока, его изменение (увеличение или уменьшение) или если катушки движутся относительно друг друга. Направление отклонения стрелки гальванометра противоположны при включении и выключении тока (уменьшении – увеличении силы тока).
При обобщении результатов своих экспериментов Фарадей отметил, что индукционный ток возникает всякий раз, когда происходит изменение потока магнитной индукции, сцепленного с контуром. При этом величина индукционного тока не связана со способом изменения потока, а зависит от скорости его изменения. Эмпирически Фарадей доказывал, что величина угла отклонения стрелки гальванометра связана со скоростью перемещения магнита (скоростью изменения силы тока, скоростью перемещения катушек относительно друг друга).
При этом величина индукционного тока не связана со способом изменения потока, а зависит от скорости его изменения. Эмпирически Фарадей доказывал, что величина угла отклонения стрелки гальванометра связана со скоростью перемещения магнита (скоростью изменения силы тока, скоростью перемещения катушек относительно друг друга).
Своими опытами Фарадей показал, что сила тока индукции в проводящем контуре пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность, которую ограничивает рассматриваемый контур.
На основе опытов Фарадея Максвелл сформулировал основной закон электромагнитной индукции. В соответствии с этим законом электродвижущая сила индукции в замкнутом контуре равна скорости изменения магнитного потока () сквозь поверхность, которую ограничивает этот контур:
где , – магнитный поток ( – угол между вектором и нормалью к плоскости контра). Минус отображает правило Ленца.
Значение опытов Фарадея заключено в том, что через явления электромагнитной индукции проявляется взаимосвязь электрического и магнитного полей. Электрическое поле, которое возникает при изменении магнитного поля, имеет иную природу, нежели электростатическое поле. Оно не имеет непосредственной связи с электрическими зарядами, и его линии напряженности не могул на них начинаться и заканчиваться. Эти линии поля подобны линиям магнитной индукции и являются замкнутыми линиями. Это электрическое поле является вихревым.
Электрическое поле, которое возникает при изменении магнитного поля, имеет иную природу, нежели электростатическое поле. Оно не имеет непосредственной связи с электрическими зарядами, и его линии напряженности не могул на них начинаться и заканчиваться. Эти линии поля подобны линиям магнитной индукции и являются замкнутыми линиями. Это электрическое поле является вихревым.
Примеры решения задач
Разработка урока»Опыты Фарадея. Электромагнитная индукция». Лабораторная работа «Исследование явления электромагнитной индукции».
Учитель физики ГБОУ СОШ №58 г. Севастополя Сафроненко Н.И.
Тема урока: Опыты Фарадея. Электромагнитная индукция.
Лабораторная работа «Исследование явления электромагнитной индукции»
Цели урока: Знать/понимать: определение явления электромагнитной индукции. Уметь описывать и объяснять электромагнитную индукцию, уметь проводить наблюдения природных явлений, использовать простые измерительные приборы для изучения физических явлений.
— развивающая: развивать логическое мышление, познавательный интерес, наблюдательность.
— воспитательная: Формировать убеждённость в возможности познания природы, необходимость разумного использования достижений науки для дальнейшего развития человеческого общества, уважения к творцам науки и техники.
Оборудование: Электромагнитная индукция : катушка с гальванометром, магнит, катушка с сердечником, источник тока, реостат, катушка с сердечником по которой течет переменный ток, сплошное и кольцо с прорезью, катушка с лампочкой. Фильм о М.Фарадее.
Тип урока: комбинированный урок
Метод урока: частично-поисковый, объяснительно-иллюстративный
Домашнее задание:
§21(стр.90-93), устно отвечать на вопросы стр.90, тест 11 стр.108
(автор учебника Кабардин)
Лабораторная работа
Исследование явления электромагнитной индукции
Цель работы: выяснить
1)при каких условиях в замкнутом контуре (катушке) возникает индукционный ток;
2)от чего зависит направление индукционного тока;
3)от чего зависит сила индукционного тока.
Оборудование: миллиамперметр, катушка, магнит
Ход урока.
Соедините концы катушки с клеммами миллиамперметра.
1. Выясните, что электрический ток (индукционный) в катушке возникает при изменении магнитного поля внутри катушки. Изменения магнитного поля внутри катушки можно вызвать, вдвигая магнит в катушку или удаляя его из неё.
А)Введите магнит южным полюсом в катушку, а затем удалите.
Б) Введите магнит северным полюсом в катушку, а затем удалите.
При движении магнита появился ток (индукционный) в катушке? (При изменении магнитного поля внутри катушки появился индукционный ток?)
2. Выясните, что направление индукционного тока зависит от направления движения магнита относительно катушки (вносят магнит или удаляют) и от того каким полюсом вносят или удаляют магнит.
А)Введите магнит южным полюсом в катушку, а затем удалите.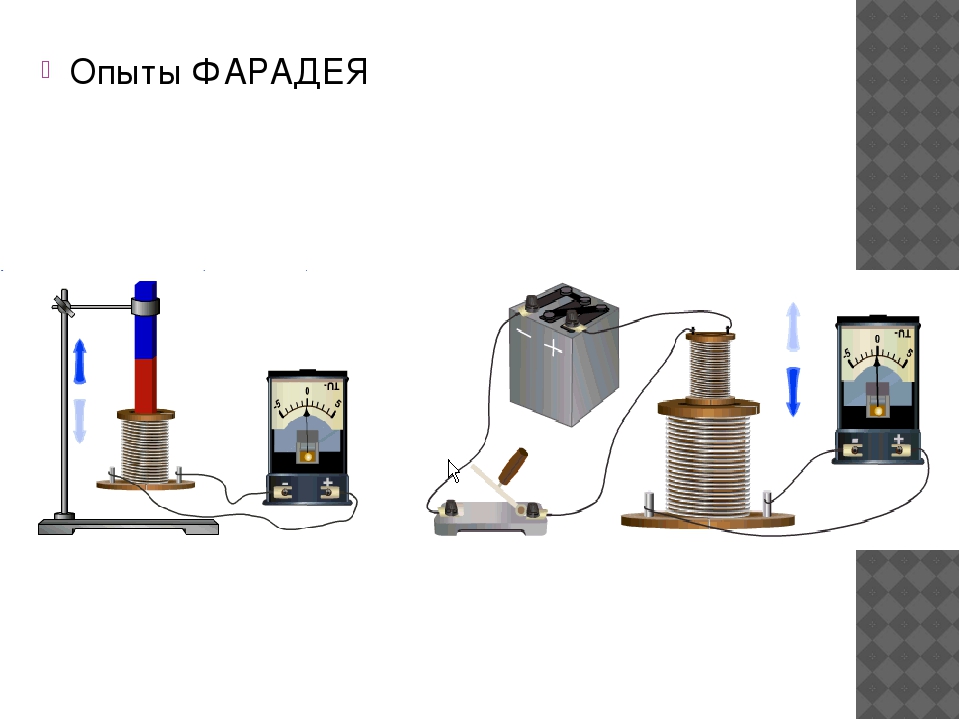 Пронаблюдайте, что происходит со стрелкой миллиамперметра в обоих случаях.
Пронаблюдайте, что происходит со стрелкой миллиамперметра в обоих случаях.
Б) Введите магнит северным полюсом в катушку, а затем удалите. Пронаблюдайте, что происходит со стрелкой миллиамперметра в обоих случаях. Нарисуйте направления отклонения стрелки миллиамперметра:
Полюса магнита
В катушку
Из катушки
Южный полюс
Северный полюс
3. Выясните, что сила индукционного тока зависит от скорости движения магнита ( скорости изменения магнитного поля в катушке).
Медленно вводите магнит в катушку. Пронаблюдайте за показаниями миллиамперметра.
Быстро вводите магнит в катушку. Пронаблюдайте за показаниями миллиамперметра.
Вывод.
Ход урока
Дорога к знаниям? Её легко понять. Ответить можно просто: «Вы ошибаетесь и ошибаетесь опять, но меньше, меньше с каждым разом. Я выражаю надежду, что сегодняшний урок будет ещё одним меньше на этой дороге знаний. Наш урок посвящён явлению электромагнитной индукции, которое открыл английский физик Майкл Фарадей 29 августа 1831 года. Редкий случай, когда дата нового замечательного открытия известна так точно!
Наш урок посвящён явлению электромагнитной индукции, которое открыл английский физик Майкл Фарадей 29 августа 1831 года. Редкий случай, когда дата нового замечательного открытия известна так точно!
Явление электромагнитной индукции – явление возникновения электрического тока в замкнутом проводнике (катушке) при изменении внешнего магнитного поля внутри катушки. Ток называется индукционным. Индукция — наведение, получение.
Цель урока: изучить явление электромагнитной индукции, т.е. при каких условиях в замкнутом контуре (катушке) возникает индукционный ток, выяснить от чего зависит направление и величина индукционного тока.
Одновременно с изучением материала будете выполнять лабораторную работу.
В начале 19 века (1820г.) после опытов датского учёного Эрстеда стало ясно, что электрический ток создаёт вокруг себя магнитное поле. Вспомним ещё раз этот опыт. (Ученик рассказывает опыт Эрстеда). После этого встал вопрос о том, нельзя ли получить ток с помощью магнитного поля, т.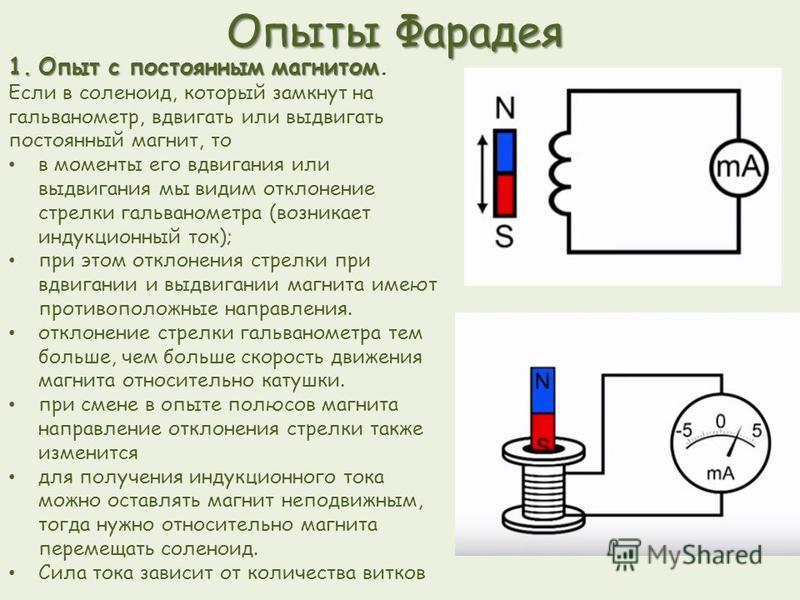 е. произвести обратные действия. В первой половине 19 века учёные обратились именно к таким опытам: стали искать возможность создания электрического тока за счёт магнитного поля. М.Фарадей в своём дневнике записал: «Превратить магнетизм в электричество». И шёл к своей цели почти десять лет. Справился с задачей блестяще. Как напоминание о том, над чем ему всё время следует думать, он носил в кармане магнит. Этим уроком мы отдадим дань уважения великому учёному.
е. произвести обратные действия. В первой половине 19 века учёные обратились именно к таким опытам: стали искать возможность создания электрического тока за счёт магнитного поля. М.Фарадей в своём дневнике записал: «Превратить магнетизм в электричество». И шёл к своей цели почти десять лет. Справился с задачей блестяще. Как напоминание о том, над чем ему всё время следует думать, он носил в кармане магнит. Этим уроком мы отдадим дань уважения великому учёному.
Вспомним Майкла Фарадея. Кто же он такой? (Ученик рассказывает о М.Фарадее).
Сын кузнеца, разносчик газет, переплётчик книг, самоучка, самостоятельно изучивший физику и химию по книгам, лаборант выдающегося химика Деви и наконец учёный, проделал большую работу, проявил изобретательность, настойчивость, упорство пока не получил электрический ток с помощью магнитного поля.
Совершим путешествие в те далёкие времена и воспроизведём опыты Фарадея. Фарадея считают крупнейшим в истории физики экспериментатором.
N S
1) 2)
S N
Магнит вводили в катушку. При движении магнита в катушке регистрировался ток (индукционный). Первая схема была довольно простой. Во-первых, М.Фарадей использовал в опытах катушку с большим числом витков. Катушка была присоединена к прибору миллиамперметру. Нужно сказать, что в те далёкие времена не было достаточно хороших инструментов для измерения электрического тока. Поэтому пользовались необычным техническим решением: брали магнитную стрелку, располагали рядом с ней проводник, по которому протекал ток, и по отклонению магнитной стрелки судили о протекающем токе. Мы будем судить о токе по показаниям миллиамперметра.
Учащиеся воспроизводят опыт, выполняют п.1 в лабораторной работе. Обратили внимание, что стрелка миллиамперметра отклоняется от своего нулевого значения, т.е. показывает, что в цепи появился ток тогда, когда магнит движется. Стоит магниту остановиться, как стрелка возвращается в нулевое положение, т.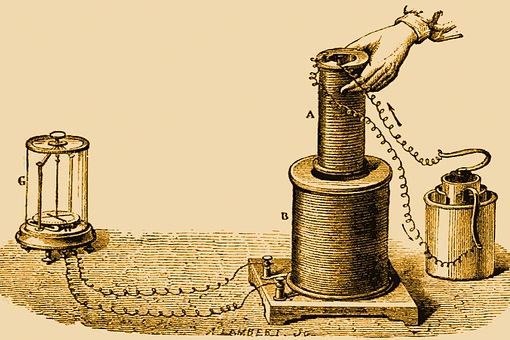 е.электрического тока в цепи нет. Ток появляется тогда, когда изменяется магнитное поле внутри катушки.
е.электрического тока в цепи нет. Ток появляется тогда, когда изменяется магнитное поле внутри катушки.
Пришли к тому о чём говорили в начале урока: получили электрический ток с помощью изменяющегося магнитного поля. Это первая заслуга М. Фарадея.
Вторая заслуга М. Фарадея — установил от чего зависит направление индукционного тока. Установим и мы это. Учащиеся выполняют п.2 в лабораторной работе. Обратимся к п.3 лабораторной работы. Выясним, что сила индукционного тока зависит от скорости движения магнита (скорости изменения магнитного поля в катушке).
Какие выводы сделал М.Фарадей?
Электрический ток появляется в замкнутой цепи тогда, когда магнитное поле изменяется (если магнитное поле существует, но не меняется, то тока нет).
Направление индукционного тока зависит от направления движения магнита и его полюсов.
Сила индукционного тока пропорциональна скорости изменения магнитного поля.
Второй эксперимент М.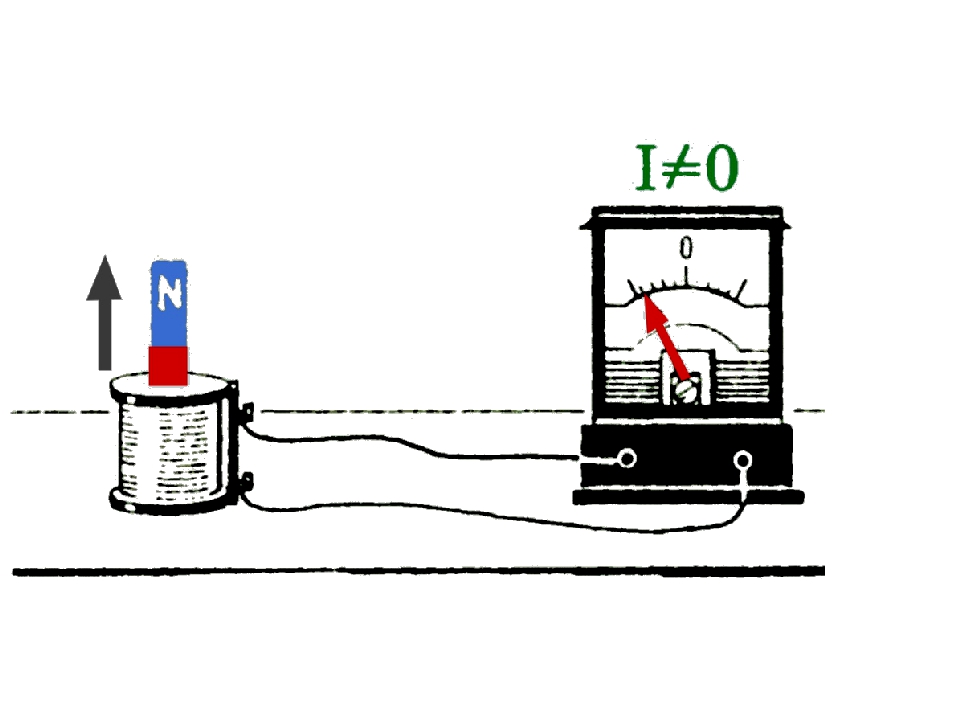 Фарадея:
Фарадея:
Взял две катушки на общем сердечнике. Одну подсоединил к миллиамперметру, а вторую с помощью ключа к источнику тока. Как только цепь замыкалась миллиамперметр показывал индукционный ток. Размыкалась тоже показывал ток. Пока цепь замкнута, т.е. в цепи идёт ток, миллиамперметр не показывал ток. Магнитное поле существует, но не меняется.
Рассмотрим современный вариант опытов М.Фарадея. В катушку соединённую с гальванометром вносим и выносим электромагнит, сердечник, включаем и выключаем ток, с помощью реостата меняем силу тока. На сердечник катушки, по которой течёт переменный ток надевают катушку с лампочкой.
Выяснили условия возникновения в замкнутой цепи (катушке) индукционного тока. А что является причиной его возникновения? Вспомним условия существования электрического тока. Это: заряженные частицы и электрическое поле. Дело в том, что изменяющееся магнитное поле порождает в пространстве электрическое поле (вихревое), которое действует на свободные электроны в катушке и приводит их в направленное движение, создавая таким образом индукционный ток.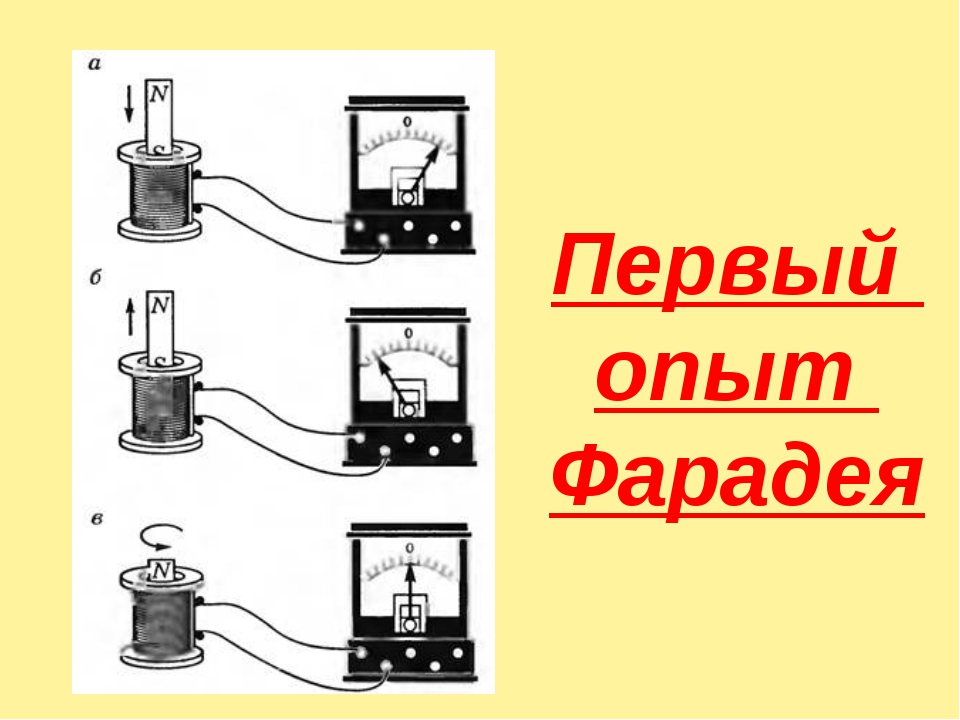
Изменяется магнитное поле, изменяется количество силовых линий магнитного поля через замкнутый контур. Если вращать рамку в магнитном поле, то в ней появится индукционный ток. Показать модель генератора.
Открытие явления электромагнитной индукции имело огромное значение для развития техники, для создания генераторов, с помощью которых вырабатывается электрическая энергия, которые стоят на энергетических промышленных предприятиях (электростанциях). Демонстрируется фильм о М.Фарадее «От электричества до электрогенераторов» с 12.02 минуты.
На явлении электромагнитной индукции работают трансформаторы, с помощью которых передают электроэнергию без потерь. Демонстрируется линия электропередачи.
Явление электромагнитной индукции используется в работе дефектоскопа, с помощью которого исследуют стальные балки, рельсы (неоднородности в балке искажают магнитное поле и в катушке дефектоскопа возникает индукционный ток).
Хочется вспомнить слова Гельмгольца: «Пока люди будут пользоваться благами электричества, они будут помнить имя Фарадея».
«Да будут святы те, кто в творческом пылу, исследуя весь мир, открыли в нём законы».
Я думаю, что на нашей дороге знаний ошибок стало ещё меньше.
Что нового узнали? (Что ток можно получить с помощью изменяющегося магнитного поля. Выяснили от чего зависит направление и величина индукционного тока).
Чему научились? ( Получать индукционный ток с помощью изменяющегося магнитного поля).
Вопросы:
В металлическое кольцо в течении первых двух секунд вдвигают магнит, в течении следующих двух секунд он неподвижен внутри кольца, в течении следующих двух секунд его вынимают. В каких промежутках времени в катушке идёт ток? (От 1-2с; 5-6с).
На магнит надевают кольцо с прорезью и без. В каком возникает индукционный ток? (В замкнутом кольце)
На сердечнике катушки, которая подключена к источнику переменного тока, находится кольцо. Включают ток и кольцо подпрыгивает. Почему?
Оформление доски:
Опыты Фарадея. Электромагнитная индукция (29 августа 1831г.)
Электромагнитная индукция (29 августа 1831г.)
«Превратить магнетизм в электричество»
М.Фарадей
Портрет М.Фарадея
Рисунки опытов М.Фарадея.
Электромагнитная индукция – явление возникновения электрического тока в замкнутом проводнике (катушке) при изменении внешнего магнитного поля внутри катушки.
Этот ток называется индукционным.
Открытый урок «Явление электромагнитной индукции. Опыты Фарадея. Закон Ленца»
Задачи урока:
- изучить явление электромагнитной индукции и
условия его возникновения; - рассмотреть историю вопроса о связи магнитного
поля и электрического; - показать причинно-следственные связи при
наблюдении явления электромагнитной индукции,
раскрыть отношения явления и его сущности при
постановке опытов; - продолжить формирование изменений, наблюдать,
выделять главное, объяснять увиденное.
Оборудование: разборный школьный
трансформатор, гальванометр, постоянный магнит,
аккумулятор, источник переменного тока, реостат,
ключ, замкнутый виток с низковольтной лампой,
соединительные провода, стержень с двумя
алюминиевыми кольцами на концах, одно из которых
сплошное, другое с разрезом, портрет М.Фарадея,
телевизор, в/ф «Явление электромагнитной
индукции», карточки-задания, кроссворды, ребус,
криптограмма, оборудование для опытов.
I. Оргмомент.
II. Мотивация учебной деятельности
Учитель. Мы с вами прошли тему
«Электромагнетизм». Сегодня нам предстоит
выяснить, как вы усвоили этот материал. Обобщим
знания о магнитном поле, будет совершенствовать
умения объяснять магнитные явления. Раскроем
особенные и общие черты магнитного и
электрического полей, проведем контроль знаний,
продолжим формирование умений наблюдать,
обобщать, синтезировать изученное.
III. Практическая работа -КМД-
Класс делится на 4 группы. Они работают так:
Первая группа – пишет физический диктант. (Приложение
1.)
Вторая группа – решает кроссворд. (Приложение 2.)
Третья группа – решает качественные задачи. (Приложение
3.)
И получают баллы за каждую работу. Потом
обмениваются между собой заданиями.
Четвертая группа – четверо играют в карты.
Пока они готовятся, желающие получить жетоны,
правильно отвечают на поставленные вопросы:
– В каком месте Земли магнитная стрелка обоими
концами показывает на юг? (На северном
географическом полюсе)
– Если поднести несколько раз к часам сильный
магнит, то показания часов будут неправильными.
Как объяснить это? (Стальная пружина и другие
стальные детали часов, намагничиваясь,
взаимодействуют друг с другом, вследствие чего
правильный ход часов нарушается)
– Где ошибка?
– Правильно ли указано направление тока?
Учитель. А вот, что написал о магнитных
А вот, что написал о магнитных
явлениях Д.И. Менделеев, мы сможем сказать, если
расшифруем, что здесь написано. (Приложение 3).
К доске идет…
Решение задач.
IV. Изучение нового материала
Учитель. Ранее в электродинамике изучались
явления, связанные или обусловленные
существованием постоянных во времени
(статических и стационарных) электрических и
магнитных полей. Появляются ли новые явления при
наличии переменных полей? Впервые явление,
вызванное переменным магнитным полем, наблюдал в
1831году М.Фарадей. Он решал ПРОБЛЕМУ: может ли
магнитное поле вызвать появление электрического
тока в проводнике? А теперь посмотрим опыты и
послушаем объяснение их.
По итогам зачета объявляются оценки и
комментируются.
Учитель. А сейчас переходим к изучению
новой темы. Цель урока мы узнаем, если разгадаем
ребус. (Приложение 2) Да, да! Именно эти
слова записал Майкл Фарадей в своем дневнике в 1822
году. «Превратить магнетизм в
«Превратить магнетизм в
электричество». После открытия Эрстедом в 1820
году магнитного поля, было установлено, что
магнитное поле и эл.ток всегда существуют
одновременно. Фарадей, зная о тесной связи между
током и магнитном полем, был уверен, что с помощью
магнитного поля можно создать в замкнутом
проводнике эл.ток. Он провёл многочисленные
опыты и доказал это, открыв в 1831году явление
электромагнитной индукции.
С биографией М.Фарадея нас познакомит студент …
V. Демонстрация опытов Фарадея.
Учитель. Рассмотрим опыты Фарадея, с
помощью которых он открыл явление
электромагнитной индукции.
1. Возьмем соленоид, соединенный с
гальванометром (рис. 1), и будем вдвигать в него
постоянный магнит. Оказывается, что при движении
магнита стрелка гальванометра отклоняется. Если
же магнит останавливается, то стрелка
гальванометра возвращается в нулевое положение.
То же самое получается при выдвижении магнита из
соленоида или при надевании соленоида на
неподвижный магнит. Такие опыты показывают, что
Такие опыты показывают, что
индукционный ток возникает в соленоиде только
при относительном перемещении соленоида и
магнита.
Рис. 1
2. Будем опускать в соленоид В катушку с
током А (рис. 2). Оказывается, что и в этом
случае в соленоиде В возникает индукционный
ток только при относительном перемещении
соленоида В и катушки А.
Рис. 2
3. Вставим катушку А в соленоид В и
закрепим их неподвижно (рис. 3). При этом тока в
соленоиде нет. Но в моменты замыкания или
размыкания цепи катушки А в соленоиде В
появляется индукционный ток. То же самое
Рис. 3
Рис. 4
получается в моменты усиления или ослабления
тока в катушке А с помощью изменения
сопротивления R.
В дальнейшем цепь катушки А, соединенную с
источником электрической энергии, будем
называть первичной, а цепь соленоида В, в
которой возникает индукционный ток, – вторичной.
Эти же названия будем применять и к самим
катушкам.
4. Включим первичную катушку в сеть переменного
тока, а вторичную катушку соединим с лампой
накаливания (рис. 4). Оказывается, лампа
непрерывно горит, пока в первичной катушке течет
переменный ток.
Нетрудно заметить, что общим для всех описанных
опытов является изменение магнитного поля в
соленоиде, которое и создает в нем индукционный
ток.
Выясним теперь, всякое ли изменение магнитного
поля вокруг замкнутого контура наводит в нем
индукционный ток. Возьмем плоский контур в виде
рамки, соединенной с гальванометром. Поместим
рядом с рамкой магнит так, чтобы его линии
индукции не проходили внутри рамки, а находились
в ее плоскости (рис. 5а).
5а).
Рис. 5
Оказывается, что при перемещении рамки или
магнита вдоль плоскости рисунка стрелка
гальванометра не отклоняется. Если же рамку
поворачивать вокруг оси 00′ (рис. 5б), то в
ней возникает индукционный ток.
На основании описанных опытов можно сделать
следующий вывод: индукционный ток (и э. д. с.
индукции) в замкнутом контуре появляется только
в том случае, когда изменяется магнитный поток,
который проводит через площадь, охваченную
контуром.
С помощью этого явления может получится эл. ток
практически любой мощности, а это позволяет
широко использовать эл. энергию в
промышленности. Получается она в основном с
помощью индукционных генераторов, принцип
работы которых основан на явлении эл-магнитной
индукции. Поэтому Фарадей по праву считается
одним из основателей электротехники.
Рассмотрим подробнее явление электромагнитной
индукции.
Пусть в однородном магнитном поле с индукцией В
находится прямолинейный металлический
проводник длиной L.
Приведем этот проводник в движение со скоростью так, что бы угол
между векторами В и составлял 90 градусов, то вместе с
проводником будут направленно двигаться и его
собственные электроны, так как их движение
происходит в магнитном поле, то на них должна
действовать сила Лоренца.
С помощью правила левой руки можно установить,
что свободные электроны будут смещаться к концу
А. И тогда между А и В возникает напряжение U ,
которое создаст в нем эл. силу Fэл., которая
уравновесит Fл. Fэл.= Fл., в этом случае смещение
электронов прекратится.
Fэл.= Е . q = U/L . q, а Fл.= В .
. q .
sinU/L . q = В . . q . sinU = В .
. L .
sin, но напряжение на полюсах при разомкнутой цепи
= Е.
Еинд.= В . . L . sin
Рис. 6
А если проводник включить в цепь, то в ней
возникает индукционный ток.
Направление индукционного тока, возникающего в
прямолинейном проводнике при его движении в
магнитном поле, определяется по правилу правой
руки (рис. 7): если правую руку расположить вдоль
проводника так, чтобы линии магнитной индукции
входили в ладонь, а отогнутый большой палец
показывал направление движения проводника, то
четыре вытянутых пальца укажут направление
индукционного тока в проводнике.
Рис. 7
VI. Закон Ленца.
Учитель. В катушке, замкнутой на
гальванометр, при перемещении магнита, возникает
индукционный ток. Как определить направление
Как определить направление
индукционного тока? По правилу правой руки? (А
переломов не бойтесь!) Давайте определим это!
Индукционный ток создает собственное магнитное
поле. Связь между направлением индукционного
тока в контуре и индуцирующим магнитным полем
была установлена Ленцем.
Пусть имеется катушка, вокруг катушки существует изменяющееся
магнитное поле и оно пронизывает витки другой
катушки. А при всяком изменении магнитного поля,
пронизывающего контур замкнутого проводника, в
нем наводится индукционный ток. А как определить
направление индукционного тока? По правилу
правой руки?
Обратимся к опыту. Почему кольцо отталкивается
от магнита? А с прорезью нет? (U – тока нет.)
Значит в кольце возник ток (инд.), магнитное
поле. И можно определить поле. Поменяем полюса
магнита. И видим: что взаимодействие между
полюсами всегда препятствует движению магнита.
Ленцу удалось обобщить эту закономерность: эту
связь называют законом Ленца.
Определение: индукционный ток всегда имеет
такое направление, при котором его магнитное
поле противодействует причине его вызывающей.
Eщё раз повторим правило Ленца.
Вернемся к опыту. Стрелка гальванометра
отклоняется тем дальше, чем быстрее вдвигается в
соленоид магнит или катушка с током.
Э.д.с. индукции, возникающая в какой-либо цепи,
прямо пропорциональна скорости изменения
магнитного потока – время, за которое происходит
изменение магнитного потока. Знак минус
показывает, что когда магнитный поток
уменьшается ( –
отриц.), э.д.с. создает индукционный ток,
увеличивающий магнитный поток и наоборот.
Исходя из формулы:
1Bб = 1В 1с
VII. Закрепление материала.
Просмотр видеофильма «Электромагнитная
индукция». Решение задач.
VIII. Задание на дом.
§ 23(2-6). № 18.10, № 18.12, № 14. Повторить «Эл.ток в
газах»
IX. Итог урока.
Учитель. Спасибо вам за урок!.
Приложение 1.
Физический диктант
1. Напишите формулы для расчетов:
а) силы Лоренца;
б) магнитной проницаемости среды;
в) модуля вектора магнитной индукции;
г) магнитного потока;
д) силы Ампера;
2. Дополните следующие определения:
а) сила Лоренца – это …
б) сила Ампера – это …
в) температура Кюри – это …
г) магнитная проницаемость среды характеризует
…
3. Какая физическая величина измеряется в
теслах? Чему равна 1Тл?
4. Какими способами можно получить магнитное
поле?
5. Какие величины характеризуют это поле?
6. Какую физическую величину измеряют в веберах?
Какую физическую величину измеряют в веберах?
Чему равен 1Вб?
7. Дополните предложения:
а) У диамагнетиков они обладают свойством …
б) У ферромагнетиков их отличительные свойства …
в) У парамагнетиков для них характерно …
г) Сила Ампера применяется …
д) Электроизмерительные приборы
магнитоэлектрической системы состоят из
…………….., действуют они так:
е) Сила Лоренца используется …
–
Приложение 2.
КРОССВОРД “ДОГАДАЙТЕСЬ”
По вертикали в выделенных клетках: катушка
проводов с железным сердечником внутри. В каждую
клетку включая нумерованную напишите по букве
так чтобы по горизонтали получить слова:
1. Ученый, впервые обнаруживший взаимодействие
электрического тока и магнитные стрелки.
2. Место магнита, где наблюдаются наиболее
сильные магнитные действия.
3. Устройство, работающее на слабых токах, при
помощи которого можно управлять электрической
цепью с сильными токами.
4. Изобретатель первого в мире телеграфного
аппарата, печатающего буквы.
5 и 6. Приборы, совместное пользование которыми
позволяет передавать звук на далекие расстояния.
7. Изобретатель электромагнитного телеграфа и
азбуки из точек и тире.
8. Ученый, объяснивший намагниченность молекул
железа электрическим током.
9. Прибор, служащий для ориентации на местности,
основной частью которого является магнитная
стрелка.
10. Русский ученый, который изобрел электрический
телеграф с магнитными стрелками.
11. Одна из основных частей приборов 5 и 6,
названных выше.
12. Приемник тока, служащий для превращения
электрической энергии в механическую.
13. Вещество, из которого делают постоянные
магниты.
Приложение 3.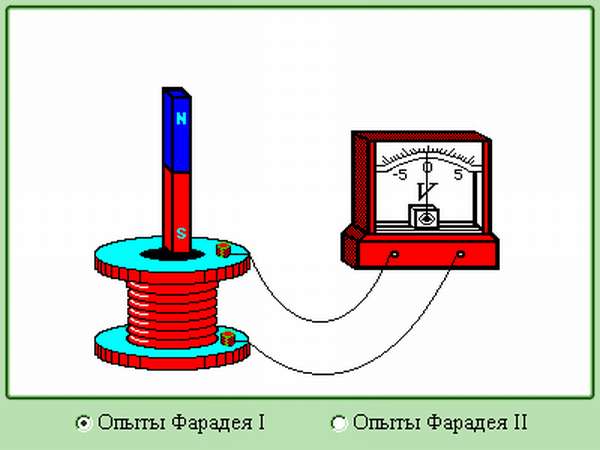
РЕБУС
Рис. 8
Прочитайте слова английского физика, которыми
он определил поставленную перед собой задачу.
Назовите ученого, год, когда эта задача была
решена, и явление которое им было открыто.
КАКОЕ СЛОВО?
Отгадайте слово по буквам, каждую из которых
надо определить, решив задачу
Рис. 9
1. Мысленно поставьте стрелку по направлению
тока на участке проводника НМ.
2. Каков номер в алфавите второй буквы слова,
покажет после включения тока северный конец
магнитной стрелки.
3. Поставьте знак направления тока в кружке
изображающем сечение проводника, и из двух
подсчетов выберите тот, который содержит этот
знак.
4. Мысленно поставьте стрелку, указывающую
направление магнитных линий внутри катушки с
током.
5. Нужная буква стоит у северного конца магнитной
стрелки.
6. Выберите букву, которая стоит у положительного
полюса источника тока.
ПРОЧТИ ФРАЗУ
Рис. 10
Зависимость эдс от магнитного потока. Разработка урока»Опыты Фарадея. Электромагнитная индукция». Лабораторная работа «Исследование явления электромагнитной индукции»
Индукционный ток это такой ток, который возникает в замкнутом проводящем контуре, находящемся в переменном магнитном поле. Этот ток может возникать в двух случаях. Если имеется неподвижный контур, пронизываемый изменяющимся потоком магнитной индукции. Либо когда в неизменном магнитном поле движется проводящий контур, что также вызывает изменение магнитного потока пронизывающего контур.
Рисунок 1 — Проводник перемещается в неизменном магнитном поле
Причиной возникновения индукционного тока является вихревое электрическое поле, которое порождается магнитным полем. Это электрическое поле действует на свободные заряды, находящиеся в проводнике, помещенном в это вихревое электрическое поле.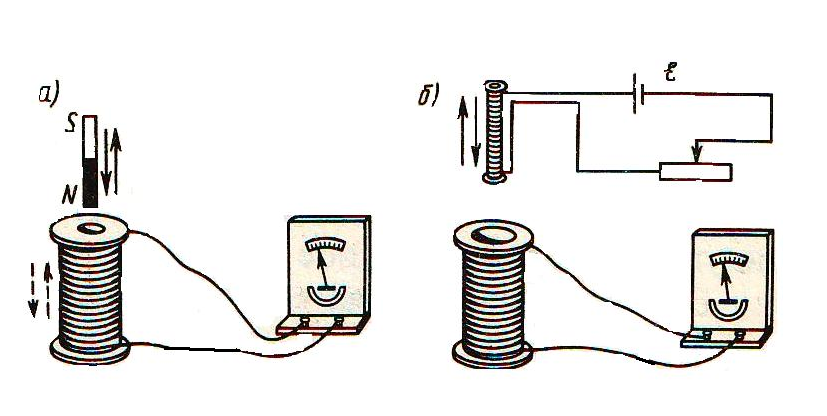
Рисунок 2 — вихревое электрическое поле
Также можно встретить и такое определение. Индукционный ток это электрический ток, который возникает вследствие действия электромагнитной индукции. Если не углубляется в тонкости закона электромагнитной индукции, то в двух словах ее можно описать так. Электромагнитная индукция это явление возникновение тока в проводящем контуре под действие переменного магнитного поля.
С помощью этого закона можно определить и величину индукционного тока. Так как он нам дает значение ЭДС, которая возникает в контуре под действие переменного магнитного поля.
Формула 1 — ЭДС индукции магнитного поля
.
Как видно из формулы 1 величина ЭДС индукции, а значит и индукционного тока зависит от скорости изменения магнитного потока пронизывающего контур. То есть чем быстрее будет меняться магнитный поток, тем больший индукционный ток можно получить. В случае, когда мы имеем постоянное магнитное поле, в котором движется проводящий контур, то величина ЭДС будет зависеть от скорости движения контура.
Чтобы определить направление индукционного тока используют правило Ленца. Которое гласит что, индукционный ток направлен навстречу тому току, который его вызвал. Отсюда и знак минус в формуле для определения ЭДС индукции.
Индукционный ток играет важную роль в современной электротехнике. Например, индукционный ток, возникающий в роторе асинхронного двигателя, взаимодействует с током, подводимым от источника питания в его статоре, вследствие чего ротор вращается. На этом принципе построены современные электродвигатели.
Рисунок 3 — асинхронный двигатель.
В трансформаторе же индукционный ток, возникающий во вторичной обмотке, используется для питания различных электротехнических приборов. Величина этого тока может быть задана параметрами трансформатора.
Рисунок 4 — электрический трансформатор.
И наконец, индукционные токи могут возникать и в массивных проводниках. Это так называемые токи Фуко. Благодаря им можно производить индукционную плавку металлов. То есть вихревые токи, текущие в проводнике вызывают его разогрев. В зависимости от величины этих токов проводник может разогреваться выше точки плавления.
То есть вихревые токи, текущие в проводнике вызывают его разогрев. В зависимости от величины этих токов проводник может разогреваться выше точки плавления.
Рисунок 5 — индукционная плавка металлов.
Итак, мы выяснили, что индукционный ток может оказывать механическое, электрическое и тепловое действие. Все эти эффекты повсеместно используются в современном мире, как в промышленных масштабах, так и на бытовом уровне.
ИНДУКЦИОННЫЙ ТОК — это электрический ток, возникающий при изменении потока магнитной индукции в замкнутом проводящем контуре. Это явление носит название электромагнитной индукции. Хотите узнать какое направление индукционного тока? Росиндуктор — это торговый информационный портал, где вы найдете информацию про ток.
Определяющее направление индукционного тока правило звучит следующим образом: «Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван». Правая рука развернута ладонью навстречу магнит¬ным силовым линиям, при этом большой палец направлен в сторону движения проводника, а четыре пальца по-казывают, в каком направлении будет течь индукционный ток. Перемещая проводник, мы перемещаем вместе с проводчиком все электроны, заключенные в нем, а при перемещении в магнитном поле электрических зарядов на них будет действовать сила по правилу левой руки.
Перемещая проводник, мы перемещаем вместе с проводчиком все электроны, заключенные в нем, а при перемещении в магнитном поле электрических зарядов на них будет действовать сила по правилу левой руки.
Направление индукционного тока, как и его величина, определяется правилом Ленца, в котором говорится, что направление индукционного тока всегда ослабляет действие фактора, возбудившего ток. При изменении потока магнитного поля через контур направление индукционного тока будет таким, чтобы скомпенсировать эти изменения. Когда магнитное поле возбуждающее ток в контуре создается в другом контуре, направление индукционного тока зависит от характера изменений: при увеличении внешнего тока индукционный ток имеет противоположное направление, при уменьшении — направлен в ту же сторону и стремиться усилить поток.
Катушка с индукционным током имеет два полюса (северный и южный), которые определяются в зависимости от направления тока: индукционные линии выходят из северного полюса. Приближение магнита к катушке вызывает появление тока с направлением, отталкивающим магнит. При удалении магнита ток в катушке имеет направление, способствующее притягиванию магнита.
Приближение магнита к катушке вызывает появление тока с направлением, отталкивающим магнит. При удалении магнита ток в катушке имеет направление, способствующее притягиванию магнита.
Индукционный ток возникает в замкнутом контуре, находящемся в переменном магнитном поле. Контур может быть как неподвижным (помещенным в изменяющийся поток магнитной индукции), так и движущимся (движение контура вызывает изменение магнитного потока). Возникновение индукционного тока обуславливает вихревое электрическое поле, которое возбуждается под воздействием магнитного поля.
О том, как создать кратковременный индукционный ток можно узнать из школьного курса физики.
Для этого есть несколько способов:
- — перемещение постоянного магнита или электромагнита относительно катушки,
- — перемещение сердечника относительно вставленного в катушку электромагнита,
- — замыкание и размыкание цепи,
- — регулирование тока в цепи.
Основной закон электродинамики (закон Фарадея) гласит, что сила индукционного тока для любого контура равна скорости изменения магнитного потока, проходящего через контур, взятой со знаком минус.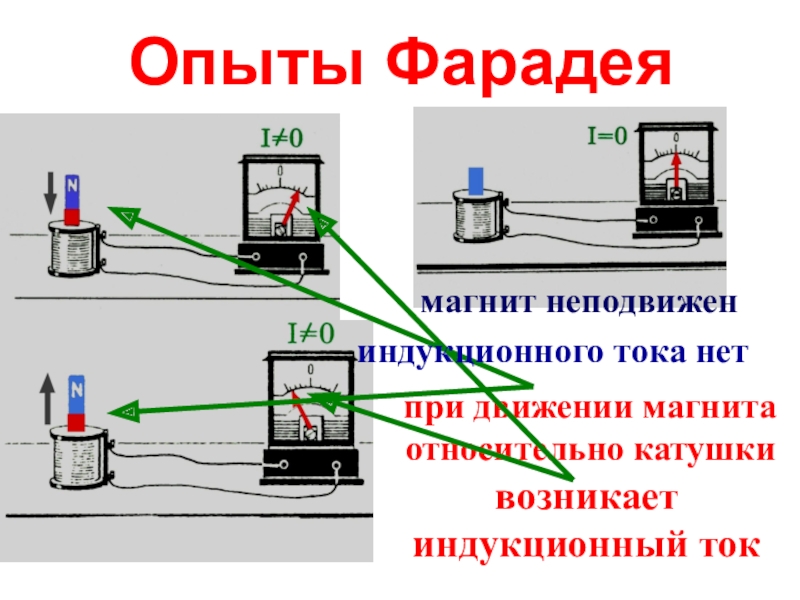 Сила индукционного тока носит название электродвижущей силы.
Сила индукционного тока носит название электродвижущей силы.
9.5. Индукционный ток
9.5.1. Тепловое действие индукционного тока
Возникновение ЭДС приводит к появлению в проводящем контуре индукционного тока
, сила которого определяется по формуле
I
i
=
|
ℰ
i
|
R
,
где ℰ
i
— ЭДС индукции, возникающая в контуре; R
— сопротивление контура.
При протекании индукционного тока в контуре выделяется теплота
, количество которой определяется одним из выражений:
Q
i
=
I
i
2
R
t
,
Q
i
=
ℰ
i
2
t
R
,
Q
i
=
I
i
|
ℰ
i
|
t
,
где I
i
— сила индукционного тока в контуре; R
— сопротивление контура; t
— время; ℰ
i
— ЭДС индукции, возникающая в контуре.
Мощность индукционного тока
вычисляется по одной из формул:
P
i
=
I
i
2
R
,
P
i
=
ℰ
i
2
R
,
P
i
=
I
i
|
ℰ
i
|
,
где I
i
— сила индукционного тока в контуре; R
— сопротивление контура; ℰ
i
— ЭДС индукции, возникающая в контуре.
При протекании индукционного тока в проводящем контуре через площадь поперечного сечения проводника переносится заряд
, величина которого вычисляется по формуле
q
i
= I
i
∆t
,
где I
i
— сила индукционного тока в контуре; Δt
— интервал времени, в течение которого по контуру течет индукционный ток.
Пример 21.
Кольцо, изготовленное из проволоки с удельным сопротивлением 50,0 ⋅ 10 −10 Ом ⋅ м, находится в однородном магнитном поле с индукцией 250 мТл. Длина проволоки равна 1,57 м, а площадь ее поперечного сечения составляет 0,100 мм 2 . Какой максимальный заряд пройдет по кольцу при выключении поля?
Решение
. Появление ЭДС индукции в кольце вызвано изменением потока вектора индукции, пронизывающего плоскость кольца, при выключении магнитного поля.
Поток индукции магнитного поля через площадь кольца определяется формулами:
- до выключения магнитного поля
Ф 1 = B
1 S
cos α,
где B
1 — первоначальное значение модуля индукции магнитного поля, B
1 = 250 мТл; S
— площадь кольца; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости кольца;
- после выключения магнитного поля
Ф 2 = B
2 S
cos α = 0,
где B
2 — значение модуля индукции после выключения магнитного поля, B
2 = 0.
∆Ф = Ф 2 − Ф 1 = −Ф 1 ,
или, с учетом явного вида Ф 1 ,
∆Ф = −B
1 S
cos α.
Среднее значение ЭДС индукции, возникающей в кольце при выключении поля,
|
ℰ
i
|
=
|
Δ
Ф
Δ
t
|
=
|
−
B
1
S
cos
α
Δ
t
|
=
B
1
S
|
cos
α
|
Δ
t
,
где ∆t
— интервал времени, за который происходит выключение поля.
Наличие ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:
I
i
=
|
ℰ
i
|
R
=
B
1
S
|
cos
α
|
R
Δ
t
,
где R
— сопротивление кольца.
При протекании индукционного тока по кольцу переносится индукционный заряд
q
i
=
I
i
Δ
t
=
B
1
S
|
cos
α
|
R
.
Максимальному значению заряда соответствует максимальное значение функции косинус (cos α = 1):
q
i
max
=
I
i
Δ
t
=
B
1
S
R
.
Полученная формула определяет максимальное значение заряда, который пройдет по кольцу при выключении поля.
Однако для расчета заряда необходимо получить выражения, которые позволят найти площадь кольца и его сопротивление.
Площадь кольца — площадь круга радиусом r
, периметр которого определяется формулой длины окружности и совпадает с длиной проволоки, из которой изготовлено кольцо:
l
= 2πr
,
где l
— длина проволоки, l
= 1,57 м.
Отсюда следует, что радиус кольца определяется отношением
r
=
l
2
π
,
а его площадь —
S
=
π
r
2
=
π
l
2
4
π
2
=
l
2
4
π
.
Сопротивление кольца задается формулой
R
=
ρ
l
S
0
,
где ρ — удельное сопротивление материала проволоки, ρ = 50,0 × × 10 −10 Ом ⋅ м; S
0 — площадь поперечного сечения проволоки, S
0 = = 0,100 мм 2 .
Подставим полученные выражения для площади кольца и его сопротивления в формулу, определяющую искомый заряд:
q
i
max
=
B
1
l
2
S
0
4
π
ρ
l
=
B
1
l
S
0
4
π
ρ
.
Вычислим:
q
i
max
=
250
⋅
10
−
3
⋅
1,57
⋅
0,100
⋅
10
−
6
4
⋅
3,14
⋅
50,0
⋅
10
−
10
=
0,625
Кл
=
625
мКл.
При выключении поля по кольцу проходит заряд, равный 625 мКл.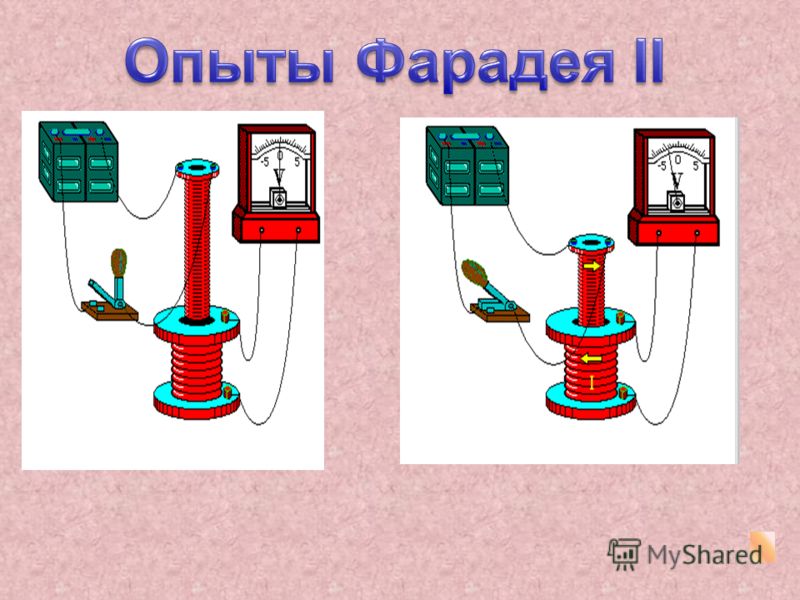
Пример 22.
Контур площадью 2,0 м 2 и сопротивлением 15 мОм находится в однородном магнитном поле, индукция которого возрастает на 0,30 мТл в секунду. Найти максимально возможную мощность индукционного тока в контуре.
Решение
. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость контура, при изменении индукции магнитного поля с течением времени.
Изменение потока вектора индукции магнитного поля определяется разностью
∆Ф = ∆BS
cos α,
где ∆B
— изменение модуля индукции магнитного поля за выбранный интервал времени; S
— площадь, ограниченная контуром, S
= 2,0 м 2 ; α — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости контура.
Среднее значение ЭДС индукции, возникающей в контуре, при изменении индукции магнитного поля:
|
ℰ
i
|
=
|
Δ
Ф
Δ
t
|
=
|
Δ
B
S
cos
α
Δ
t
|
=
Δ
B
S
|
cos
α
|
Δ
t
,
где ∆B
/∆t
— скорость изменения модуля вектора индукции магнитного поля с течением времени, ∆B
/∆t
= 0,30 мТл/с.
Появление ЭДС индукции приводит к появлению индукционного тока; сила индукционного тока определяется законом Ома:
I
i
=
|
ℰ
i
|
R
=
Δ
B
S
|
cos
α
|
R
Δ
t
,
где R
— сопротивление контура.
Мощность индукционного тока
P
i
=
I
i
2
R
=
(Δ
B
Δ
t)
2
S
2
R
cos
2
α
R
2
=
(Δ
B
Δ
t)
2
S
2
cos
2
α
R
.
Максимальному значению мощности индукционного тока соответствует максимальное значение функции косинус (cos α = 1):
P
i
max
=
(Δ
B
Δ
t)
2
S
2
R
.
Вычислим:
P
i
max
=
(0,30
⋅
10
−
3)
2
(2,0)
2
15
⋅
10
−
3
=
24
⋅
10
−
6
Вт
=
24
мкВт.
Максимальная мощность индукционного тока в данном контуре равна 24 мкВт.
МАГНИТНОЕ ПОЛЕ
Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.
В — физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).
Магнитная индукция
— векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:
Единица магнитной индукции
. В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:
СИЛА ЛОРЕНЦА
Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F А = IBlsin a
, а сила Лоренца действует на движущийся заряд:
где a
— угол между векторами B и v
.
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила м, постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:
В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,
Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.
Если напряженность электрического поля равна нулю, то сила Лоренца л равна магнитной силе м:
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.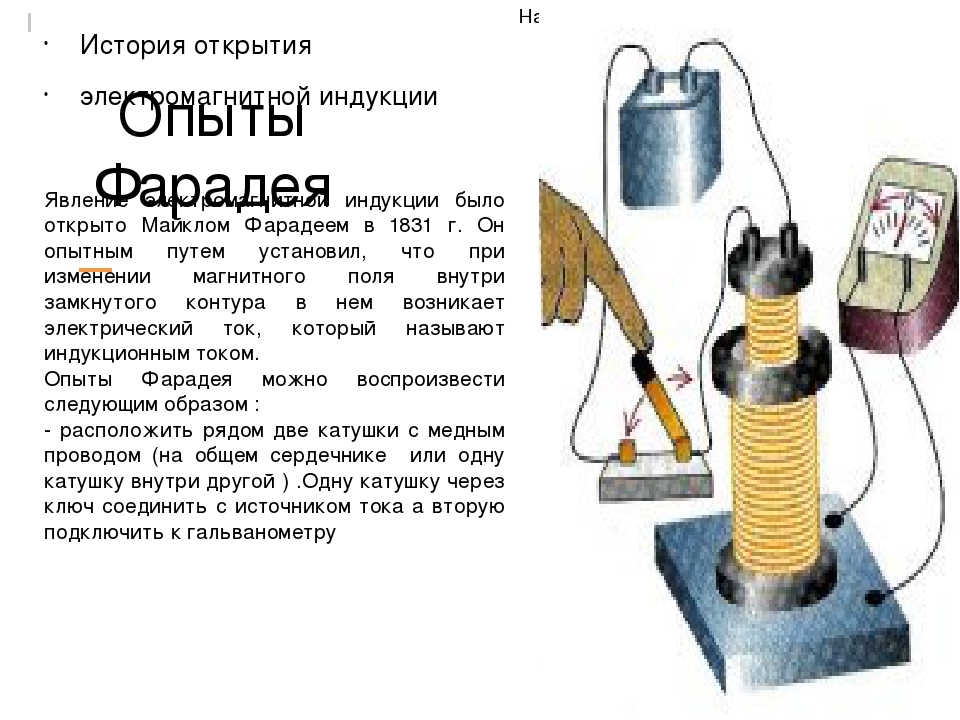
МАГНИТНЫЙ ПОТОК
Магнитный поток Ф
(поток магнитной индукции) через поверхность площадью S
— величина, равная произведению модуля вектора магнитной индукции на площадь S
и косинус угла а
между вектором и нормалью
к поверхности:
Ф=BScos
В СИ единица магнитного потока 1 Вебер (Вб) — магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:
Электромагнитная индукция
-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.
Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Опыты Фарадея показали, что сила индукционного тока I i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.
Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε i .
По закону Ома для замкнутой цепи
Так как R не зависит от , то
ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:
САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
Опыт показывает, что магнитный поток Ф
, связанный с контуром, прямо пропорционален силе тока в этом контуре:
Ф = L*I
.
Индуктивность контура L
— коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.
Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.
Самоиндукция
— явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.
Самоиндукция — частный случай электромагнитной индукции.
Индуктивность — величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени.
В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.
Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :
Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.
ЭДС самоиндукции имеет в этом случае постоянное значение:
где I — начальное значение тока, t — промежуток времени, за который сила тока убывает от I до 0.
За время t в цепи проходит электрический заряд q = I cp t
. Так как I cp = (I + 0)/2 = I/2
, то q=It/2
. Поэтому работа электрического тока:
Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:
Пример.
Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?
Энергия магнитного поля катушки W 1 = LI 1 2 /2. По определению, индуктивность катушки L = Ф/I 1 . Следовательно,
Темы кодификатора ЕГЭ
: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод
.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует
) электрический ток во второй катушке. Этот ток называется индукционным током
.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией
(т. е. «наведение электричества магнетизмом»).
2. Для подтверждения догадки о том, что индукционный ток порождается переменным
магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки
.
3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1
).
Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2
).
Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому
(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2)
Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2)
, а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер
(Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция
— это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур
.
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы
, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции
и обозначается .
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура
.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно , то скорость
изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3)
мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4)
совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
(5)
Это и есть закон электромагнитной индукции
или закон Фарадея
. Дадим его словесную формулировку.
Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея
. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока
.
Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком
. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем
.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное
магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный
магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца
. Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока
.
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)
). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против
внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)
(3)
).
Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4
). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.
Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону
, что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет
Расположение полюсов магнита при этом роли не играет
.
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна
. Это значит, что мы, приближая магнит, должны преодолевать
силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания
.
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.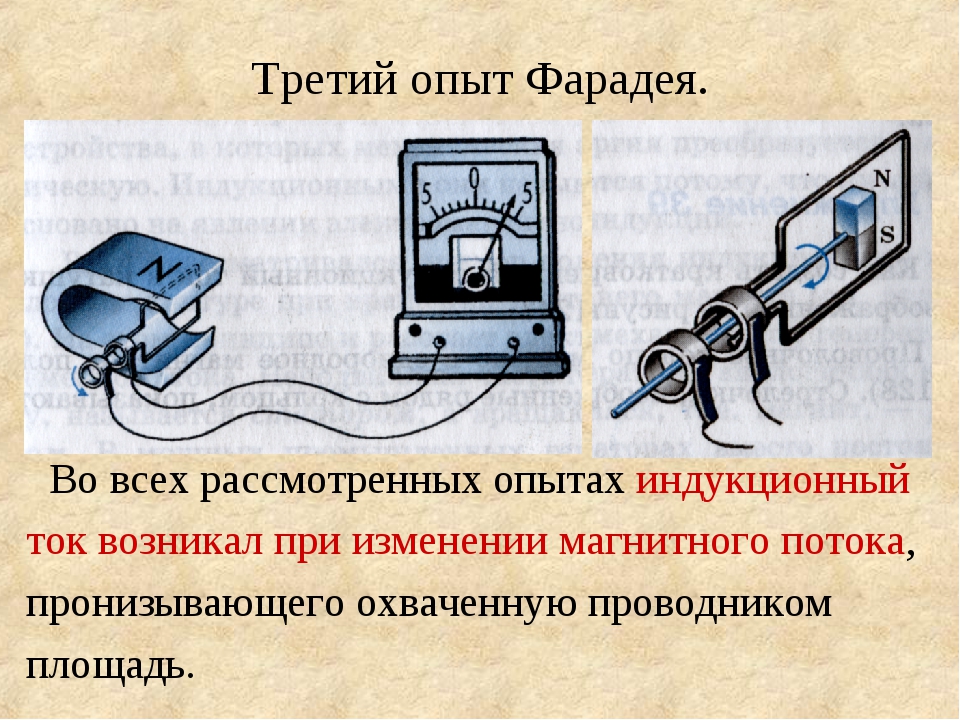
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5)
. Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5)
, величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным
. Противоположное направление обхода контура называется, соответственно, отрицательным
. Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным alt=»(\Phi > 0)»>
, если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .
ЭДС индукции считается положительной alt=»(\mathcal E_i > 0)»>
, если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: alt=»\Phi > 0″>
.
Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, alt=»\mathcal E_i > 0″>
(рис. 6
).
Рис. 6. Магнитный поток возрастает alt=»\Rightarrow \mathcal E_i > 0″>
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока
:
(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое
. Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем
. Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7
).
Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8
8
).
Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура
.
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:
Следовательно, для ЭДС индукции получаем:
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле .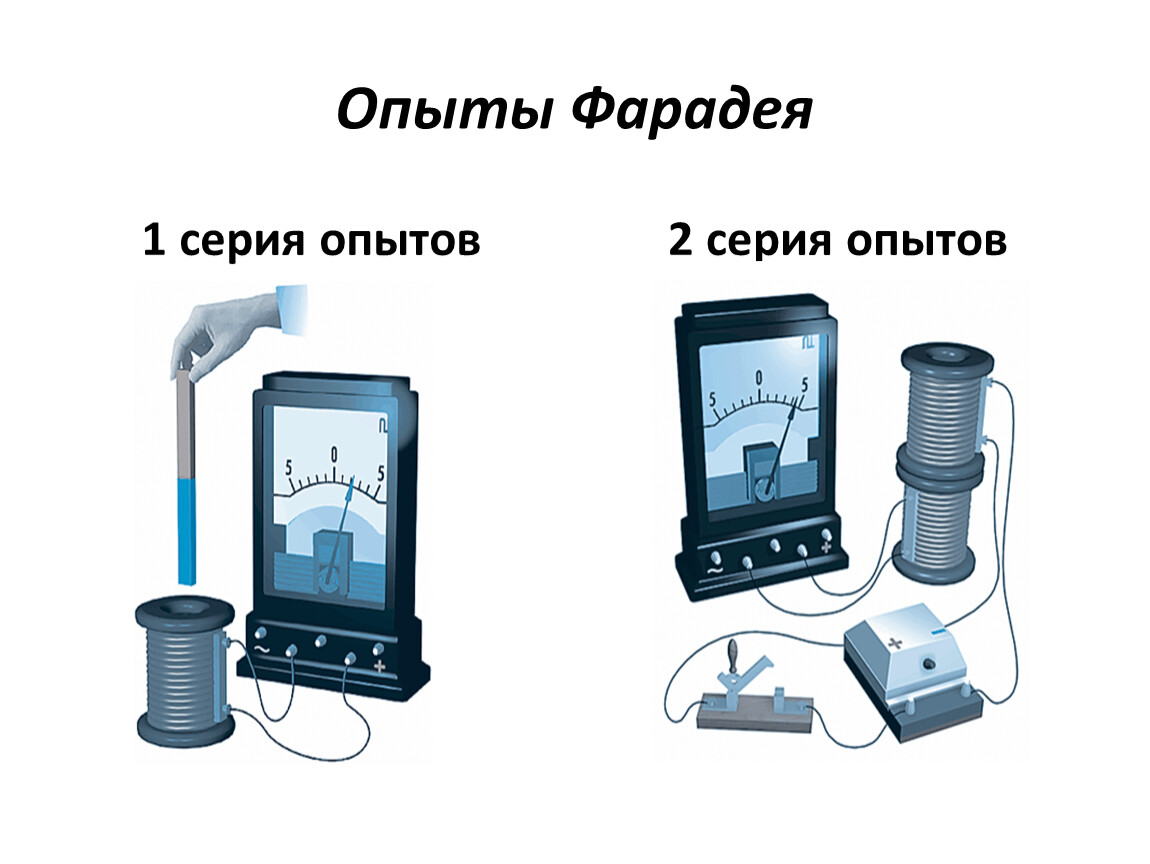 По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9
).
Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .
Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7)
.
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N
). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7)
для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9
9
). Площадь контура возрастает на величину площади прямоугольника :
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7)
. Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
«Изучение явления электромагнитной индукции». Разработка урока»Опыты Фарадея. Электромагнитная индукция». Лабораторная работа «Исследование явления электромагнитной индукции» Почему происходит изменение магнитного потока про
Цель работы:
экспериментальное изучение явления магнитной индукциии проверка правила Ленца.
Теоретическая часть:
Явление электромагнитной индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется. В нашем случае разумнее было бы менять во времени магнитное поле, так как оно создается движущимися (свободно) магнитом. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. В данном случае это мы можем наблюдать по отклонению стрелки миллиамперметра.
Оборудование:
Миллиамперметр, источник питания, катушки с сердечниками, дугообразный магнит, выключатель кнопочный, соединительные провода, магнитная стрелка (компас), реостат.
Порядок выполнения работы
I.Выяснение условий возникновения индукционного тока.
1.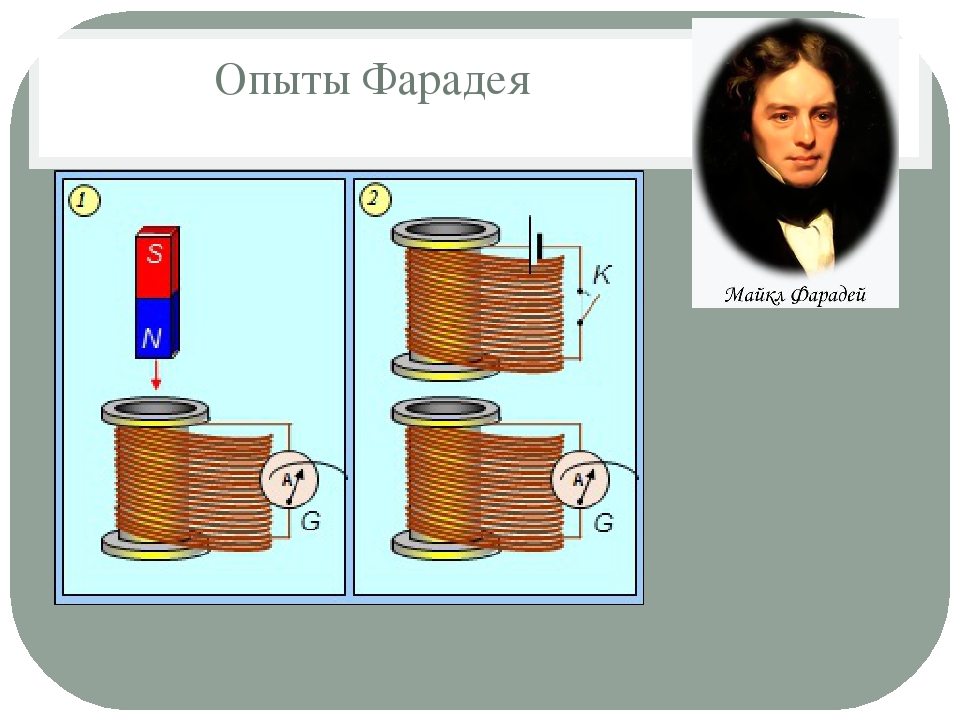 Подключите катушку-моток к зажимам миллиамперметра.
Подключите катушку-моток к зажимам миллиамперметра.
2. Наблюдая за показаниями миллиамперметра, отметьте, возникал ли индукционный ток, если:
* в неподвижную катушку вводить магнит,
* из неподвижной катушки выводить магнит,
* магнит разместить внутри катушки, оставляя неподвижным.
3. Выясните, как изменялся магнитный поток Ф, пронизывающий катушку в каждом случае. Сделайте вывод о том, при каком условии в катушке возникал индукционный ток.
II. Изучение направления индукционного тока.
1. О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра.
Проверьте, одинаковым ли будет направление индукционного тока, если:
* вводить в катушку и удалять магнит северным полюсом;
* вводить магнит в катушку магнит северным полюсом и южным полюсом.
2. Выясните, что изменялось в каждом случае. Сделайте вывод о том, от чего зависит направление индукционного тока.
III. Изучение величины индукционного тока.
1. Приближайте магнит к неподвижной катушке медленно и с большей скоростью, отмечая, на сколько делений (N
1
, N
2
)
отклоняется стрелка миллиамперметра.
2. Приближайте магнит к катушке северным полюсом. Отметьте, на сколько делений N
1
отклоняется стрелка миллиамперметра.
К северному полюсу дугообразного магнита приставьте северный полюс полосового магнита. Выясните, на сколько делений N
2
отклоняется стрелка миллиамперметра при приближении одновременно двух магнитов.
3.Выясните, как изменялся магнитный поток в каждом случае. Сделайте вывод, от чего зависит величина индукционного тока.
Ответьте на вопросы:
1.В катушку из медного провода сначала быстро, затем медленно вдвигают магнит. Одинаковый ли электрический заряд при этом переносится через сечение провода катушки?
2.Возникнет ли индукционный ток в резиновом кольце при введении в него магнита?
Цель работы: Изучить явление электромагнитной индукции.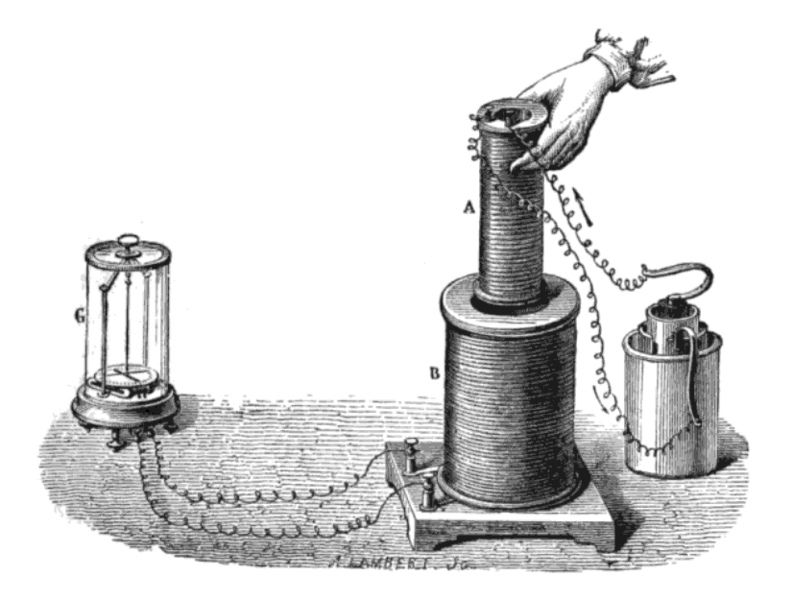
Оборудование: Миллиамперметр, катушка-моток, магнит дугообразный, источник питания, катушка с железным сердечником от разборного электромагнита, реостат, ключ, провода соединительные, модель генератора электрического тока (одна на класс).
Указания к работе:
1. Подключите катушку-моток к зажимам миллиамперметра.
2. Наблюдая за показаниями миллиамперметра, подводите один из полюсов магнита к катушке, потом на несколько секунд остановите магнит, а затем вновь приближайте его к катушке, вдвигая в неё (рис. 196). Запишите, возникал ли в катушке индукционный ток во время движения магнита относительно катушки; во время его остановки.
Запишите, менялся ли магнитный поток Ф, пронизывающий катушку, во время движения магнита; во время его остановки.
4. На основании ваших ответов на предыдущий вопрос сделайте и запишите вывод о том, при каком условии в катушке возникал индукционный ток.
5. Почему при приближении магнита к катушке магнитный поток, пронизывающий эту катушку, менялся? (Для ответа на этот вопрос вспомните, во-первых, от каких величин зависит магнитный поток Ф и, во-вторых, одинаков
ли модуль вектора индукции В магнитного поля постоянного магнита вблизи этого магнита и вдали от него. )
)
6. О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра.
Проверьте, одинаковым или различным будет направление индукционного тока в катушке при приближении к ней и удалении от неё одного и того же полюса магнита.
4. Приближайте полюс магнита к катушке с такой скоростью, чтобы стрелка миллиамперметра отклонялась не более чем на половину предельного значения его шкалы.
Повторите тот же опыт, но при большей скорости движения магнита, чем в первом случае.
При большей или меньшей скорости движения магнита относительно катушки магнитный поток Ф, пронизывающий эту катушку, менялся быстрее?
При быстром или медленном изменении магнитного потока сквозь катушку сила тока в ней была больше?
На основании вашего ответа на последний вопрос сделайте и запишите вывод о том, как зависит модуль силы индукционного тока, возникающего в катушке, от скорости изменения магнитного потока Ф, пронизывающего этукатушку.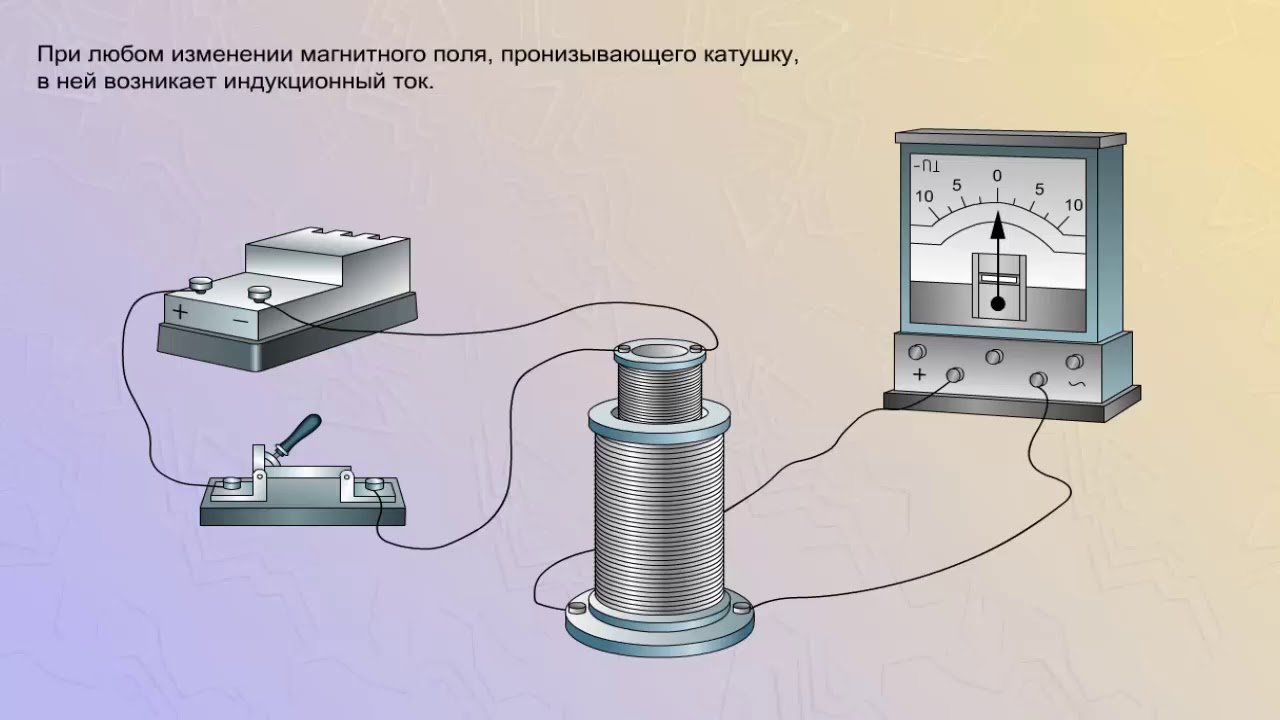
5. Соберите установку для опыта по рисунку 197.
6. Проверьте, возникает ли в катушке-мотке 1 индукционный ток в следующих случаях:
а) при замыкании и размыкании цепи, в которую включена катушка 2;
б) при протекании через катушку 2 постоянного тока;
в) при увеличении и уменьшении силы тока, протекающего через катушку 2, путём перемещения в соответствующую сторону движка реостата.
10. В каких из перечисленных в пункте 9 случаев меняется магнитный поток, пронизывающий катушку 1? Почему он меняется?
11. Пронаблюдайте возникновение электрического тока в модели генератора (рис. 198). Объясните, почему в рамке, вращающейся в магнитном поле, возникает индукционный ток.
Рис. 196
Контрольные вопросы
1.Что такое электроемкость?
2. Дайте определение следующих понятий: переменный ток, амплитуда, частота, циклическая частота, период, фаза колебаний
Лабораторная работа 11
Изучение явления электромагнитной индукции
Цель работы:
изучить явление электромагнитной индукции.
Оборудование:
миллиамперметр; катушка-моток; магнит дугообразный; источник питания; катушка с железным сердечником от разборного электромагнита; реостат; ключ; провода соединительные; модель генератора электрического тока (одна).
Ход работы
1. Подключите катушку-моток к зажимам миллиамперметра.
2. Наблюдая за показаниями миллиамперметра, подводите один из полюсов магнита к катушке, потом на несколько секунд остановите магнит, а затем вновь приближайте его к катушке, вдвигая в нее (рис). Запишите, возникал ли в катушке индукционный ток во время движения магнита относительно катушки; во время его остановки.
3. Запишите, менялся ли магнитный поток Ф, пронизывающий катушку, во время движения магнита; во время его остановки.
4. На основании ваших ответов на предыдущий вопрос сделайте и запишите вывод о том, при каком условии в катушке возникал индукционный ток.
5. Почему при приближении магнита к катушке магнитный поток, пронизывающий эту катушку, менялся? (Для ответа на этот вопрос вспомните, во-первых, от каких величин зависит магнитный поток Ф и, во-вторых, одинаков ли модуль вектора индукции В магнитного поля постоянного магнита вблизи этого магнита и вдали от него. )
)
6. О направлении тока в катушке можно судить по тому, в какую сторону от нулевого деления отклоняется стрелка миллиамперметра.
Проверьте, одинаковым или различным будет направление индукционного тока в катушке при приближении к ней и удалении от нее одного и того же полюса магнита.
7. Приближайте полюс магнита к катушке с такой скоростью, чтобы стрелка миллиамперметра отклонялась не более чем на половину предельного значения его шкалы.
Повторите тот же опыт, но при большей скорости движения магнита, чем в первом случае.
При большей или меньшей скорости движения магнита относительно катушки магнитный поток Ф, пронизывающий эту катушку, менялся быстрее?
При быстром или медленном изменении магнитного потока сквозь катушку в ней возникал больший по модулю ток?
На основании вашего ответа на последний вопрос сделайте и запишите вывод о том, как зависит модуль силы индукционного тока, возникающего в катушке, от скорости изменения магнитного потока Ф, пронизывающего эту катушку.
8.Соберите установку для опыта по рисунку.
9. Проверьте, возникает ли в катушке-мотке 1 индукционный ток в следующих случаях:
a. при замыкании и размыкании цепи, в которую включена катушка 2;
b. при протекании через катушку 2 постоянного тока;
c. при увеличении и уменьшении силы тока, протекающего через катушку 2, путем перемещения в соответствующую сторону движка реостата.
10. В каких из перечисленных в пункте 9 случаев меняется магнитный поток, пронизывающий катушку? Почему он меняется?
11. Пронаблюдайте возникновение электрического тока в модели генератора (рис.). Объясните, почему в рамке, вращающейся в магнитном поле, возникает индукционный ток.
Контрольные вопросы
1. Сформулируйте закон электромагнитной индукции.
2. Кем и когда был сформулирован закон электромагнитной индукции?
Лабораторная работа 12
Измерение индуктивности катушки
Цель работы:
Изучение основных закономерностей электрических цепей переменного тока и знакомство с простейшими способами измерения индуктивности и емкости.
Краткая теория
Под действием переменной электродвижущей силы (ЭДС) в электрической цепи, в ней возникает переменный ток.
Переменным называется такой ток, который изменяется по направлению и по величине. В данной работе рассматривается только такой переменный ток, величина которого изменяется периодически по синусоидальному закону.
Рассмотрение синусоидального тока вызвано тем обстоятельством, что все крупные электростанции вырабатывают переменные токи, весьма близкие к синусоидальным токам.
Переменный ток в металлах представляет собой движение свободных электронов то в одном, то в противоположном направлении. При синусоидальном токе характер этого движения совпадает с гармоническими колебаниями. Таким образом, синусоидальный переменный ток имеет период Т
время одного полного колебания и частоту v
число полных колебаний за единицу времени. Между этими величинами имеется зависимость
Цепь переменного тока, в отличие от цепи постоянного тока, допускает включение конденсатора.
https://pandia.ru/text/80/343/images/image073.gif» alt=»http://web-local.rudn.ru/web-local/uem/ido/8/Image443.gif»>,
называемая полным сопротивлением
или импедансом
цепи. Поэтому выражение (8) называют законом Ома для переменного тока.
В данной работе активное сопротивление R
катушки определяется при помощи закона Ома для участка цепи постоянного тока.
Рассмотрим два частных случая.
1. В цепи отсутствует конденсатор
. Это значит, что конденсатор отключается и вместо него цепь замыкается проводником, падение потенциала на котором практически равно нулю, то есть величина U
в уравнении (2) равна нулю..gif» alt=»http://web-local.rudn.ru/web-local/uem/ido/8/Image474.gif»>.
2. В цепи отсутствует катушка
: следовательно .
При из формул (6), (7) и (14) соответственно имеем
Изучением явления электромагнитной индукции занялся вплотную первым Майкл Фарадей. Точнее сказать, он установил и исследовал это явление в поисках способов превратить магнетизм в электричество.
У него на решение такой задачи ушло десять лет, мы же сейчас пользуемся плодами его труда повсеместно, и не представляем себе современную жизнь без применения электромагнитной индукции . В 8 классе, мы уже рассматривали эту тему, в 9 классе это явление рассматривается уже более детально, но вывод формул относится к курсу 10 класса. По этой ссылке вы можете перейти для ознакомления со всеми аспектами данного вопроса.
Явление электромагнитной индукции: рассмотрим опыт
Мы рассмотрим, что представляет собой явление электромагнитной индукции. Можно провести опыт, для которого понадобится гальванометр, постоянный магнит и катушка. Соединив гальванометр с катушкой, мы вдвигаем внутрь катушки постоянный магнит. При этом гальванометр покажет изменение тока в цепи.
Так как никакого источника тока у нас в цепи нет, то логично предположить, что ток возникает вследствие появления магнитного поля внутри катушки. Когда мы будем вытаскивать магнит обратно из катушки, мы увидим, что снова изменятся показания гальванометра, но его стрелка при этом отклонится в противоположную сторону. Мы опять получим ток, но уже направленный в другую сторону.
Теперь проделаем похожий опыт с теми же элементами, только при этом мы зафиксируем магнит неподвижно, а надевать на магнит и снимать с него мы теперь будем саму катушку, подсоединенную к гальванометру. Мы получим те же результаты стрелка гальванометра будет показывать нам появление тока в цепи. При этом, когда магнит неподвижен, тока в цепи нет стрелка стоит на ноле.
Можно провести измененный вариант такого же опыта, только постоянный магнит заменить электрическим, который можно включать и выключать. Мы получим схожие с первым опытом результаты при движении магнита внутри катушки. Но, кроме того, при выключении и выключении неподвижного электромагнита, он будет вызывать кратковременное появление тока в цепи катушки.
Катушку можно заменить проводящим контуром и проделать опыты по перемещению и вращению самого контура в постоянном магнитном поле, либо же магнита внутри неподвижного контура. Результаты будут те же появление тока в цепи при движении магнита или контура.
Изменение магнитного поля вызывает появление тока
Из всего этого следует вывод, что изменение магнитного поля вызывает появление электрического тока в проводнике . Ток этот ничем не отличается от тока, который мы можем получить от батареек, например. Но чтобы указать причину его возникновения, такой ток назвали индукционным.
Во всех случаях у нас менялось магнитное поле, а точнее, магнитный поток через проводник, вследствие чего и возникал ток. Таким образом, можно вывести следующее определение:
При всяком изменении магнитного потока, пронизывающего контур замкнутого проводника, в этом проводнике возникает электрический ток, существующий в течение всего процесса изменения магнитного потока.
На этом уроке мы проведем лабораторную работу №4 «Изучение явления электромагнитной индукции». Целью этого занятия будет изучение явления электромагнитной индукции. С помощью необходимого оборудования мы проведем лабораторную работу, в конце которой узнаем, как правильно изучать и определять это явление.
Целью этого занятия будет изучение явления электромагнитной индукции. С помощью необходимого оборудования мы проведем лабораторную работу, в конце которой узнаем, как правильно изучать и определять это явление.
Цель — изучение явления электромагнитной индукции
.
Оборудование:
1. Миллиамперметр.
2. Магнит.
3. Катушка-моток.
4. Источник тока.
5. Реостат.
6. Ключ.
7. Катушка от электромагнита.
8. Соединительные провода.
Рис. 1. Экспериментальное оборудование
Начнем лабораторную работу со сбора установки. Чтобы собрать схему, которую мы будем использовать в лабораторной работе, присоединим моток-катушку к миллиамперметру и используем магнит, который будем приближать или удалять от катушки. Одновременно с этим мы должны вспомнить, что будет происходить, когда будет появляться индукционный ток.
Рис. 2. Эксперимент 1
2. Эксперимент 1
Подумайте над тем, как объяснить наблюдаемое нами явление. Каким образом влияет магнитный поток на то, что мы видим, в частности происхождение электрического тока. Для этого посмотрите на вспомогательный рисунок.
Рис. 3. Линии магнитного поля постоянного полосового магнита
Обратите внимание, что линии магнитной индукции выходят из северного полюса, входят в южный полюс. При этом количество этих линий, их густота различна на разных участках магнита. Обратите внимание, что направление индукции магнитного поля тоже изменяется от точки к точке. Поэтому можно сказать, что изменение магнитного потока приводит к тому, что в замкнутом проводнике возникает электрический ток, но только при движении магнита, следовательно, изменяется магнитный поток, пронизывающий площадь, ограниченную витками этой катушки.
Следующий этап нашего исследования электромагнитной индукции связан с определением направления индукционного тока
. О направлении индукционного тока мы можем судить по тому, в какую сторону отклоняется стрелка миллиамперметра.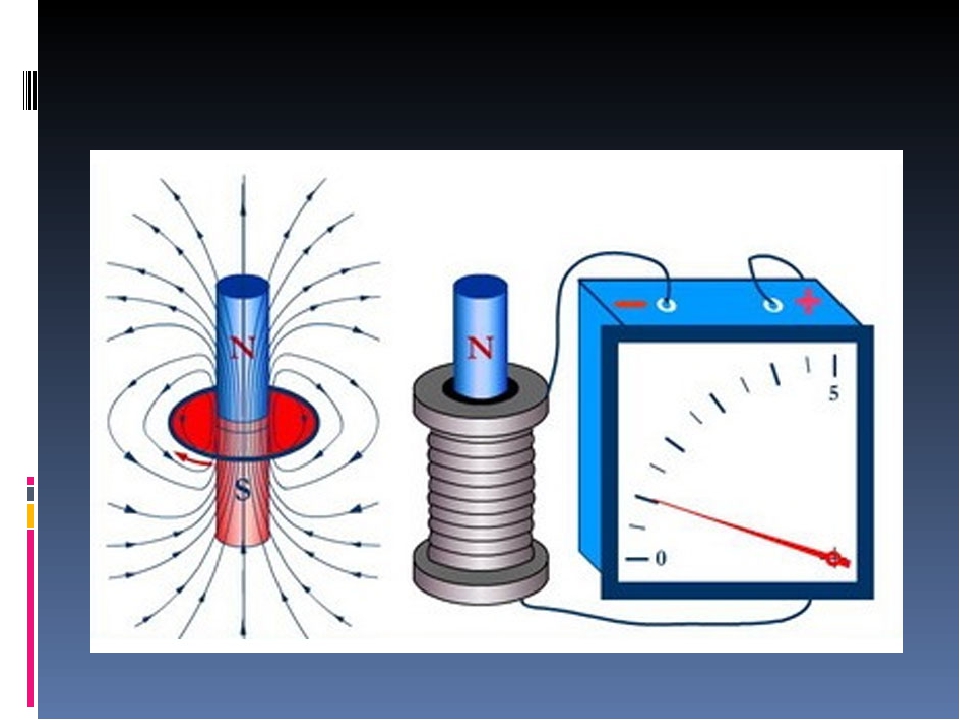 Воспользуемся дугообразным магнитом и увидим, что при приближении магнита стрелка отклонится в одну сторону. Если теперь магнит двигать в другую сторону, стрелка отклонится в другую сторону. В результате проведенного эксперимента мы можем сказать, что от направления движения магнита зависит и направление индукционного тока. Отметим и то, что от полюса магнита тоже зависит направление индукционного тока.
Воспользуемся дугообразным магнитом и увидим, что при приближении магнита стрелка отклонится в одну сторону. Если теперь магнит двигать в другую сторону, стрелка отклонится в другую сторону. В результате проведенного эксперимента мы можем сказать, что от направления движения магнита зависит и направление индукционного тока. Отметим и то, что от полюса магнита тоже зависит направление индукционного тока.
Обратите внимание, что величина индукционного тока зависит от скорости перемещения магнита, а вместе с тем и от скорости изменения магнитного потока.
Вторая часть нашей лабораторной работы связана будет с другим экспериментом. Посмотрим на схему этого эксперимента и обсудим, что мы будем теперь делать.
Рис. 4. Эксперимент 2
Во второй схеме в принципе ничего не изменилось относительно измерения индукционного тока. Тот же самый миллиамперметр, присоединенный к мотку катушки. Остается все, как было в первом случае. Но теперь изменение магнитного потока мы будем получать не за счет движения постоянного магнита, а за счет изменения силы тока во второй катушке.
В первой части будем исследовать наличие индукционного тока
при замыкании и размыкании цепи. Итак, первая часть эксперимента: мы замыкаем ключ. Обратите внимание, ток нарастает в цепи, стрелка отклонилась в одну сторону, но обратите внимание, сейчас ключ замкнут, а электрического тока миллиамперметр не показывает. Дело в том, что нет изменения магнитного потока, мы уже об этом говорили. Если теперь ключ размыкать, то миллиамперметр покажет, что направление тока изменилось.
Во втором эксперименте мы проследим, как возникает индукционный ток
, когда меняется электрический ток во второй цепи.
Следующая часть опыта будет заключаться в том, чтобы проследить, как будет изменяться индукционный ток, если менять величину тока в цепи за счет реостата. Вы знаете, что если мы изменяем электрическое сопротивление в цепи, то, следуя закону Ома, у нас будет меняться и электрический ток. Раз изменяется электрический ток, будет изменяться магнитное поле. В момент перемещения скользящего контакта реостата изменяется магнитное поле, что приводит к появлению индукционного тока.
В заключение лабораторной работы мы должны посмотреть на то, как создается индукционный электрический ток в генераторе электрического тока.
Рис. 5. Генератор электрического тока
Главная его часть — это магнит, а внутри этих магнитов располагается катушка с определенным количеством намотанных витков. Если теперь вращать колесо этого генератора в обмотке катушки будет наводиться индукционный электрический ток. Из эксперимента видно, что увеличение числа оборотов приводит к тому, что лампочка начинает гореть ярче.
Список дополнительной литературы:
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н. Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 347-348. Мякишев Г.Я. Физика: Электродинамика. 10-11 классы. Учебник для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков.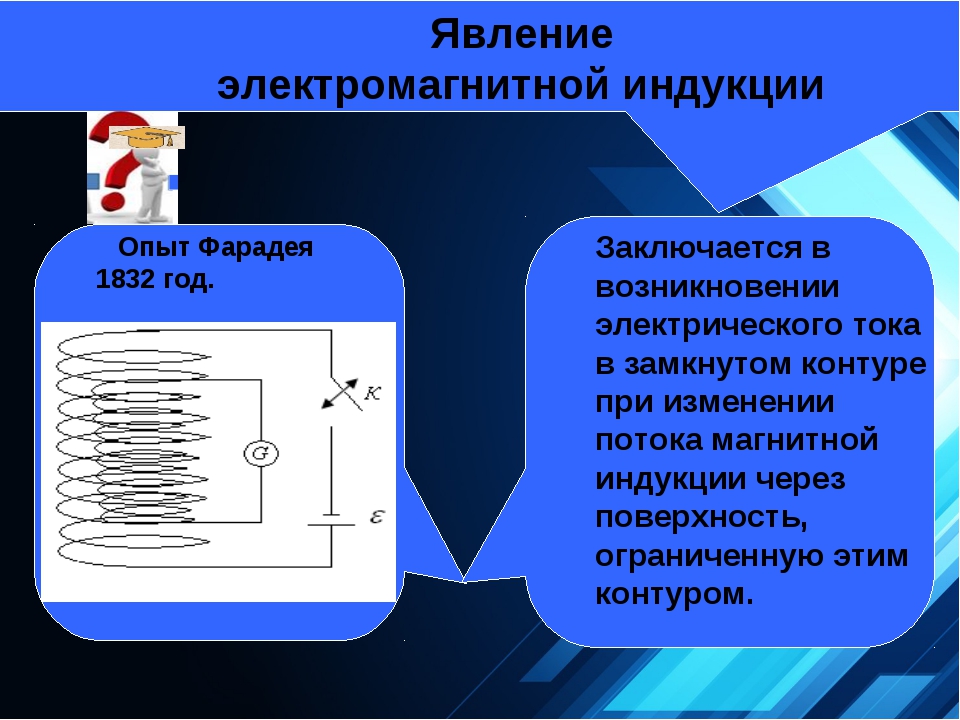 — М.: Дрофа, 2005. — 476с. Пурышева Н.С. Физика. 9 класс. Учебник. / Пурышева Н.С., Важеевская Н.Е., Чаругин В.М. 2-е изд., стереотип. — М.: Дрофа, 2007.
— М.: Дрофа, 2005. — 476с. Пурышева Н.С. Физика. 9 класс. Учебник. / Пурышева Н.С., Важеевская Н.Е., Чаругин В.М. 2-е изд., стереотип. — М.: Дрофа, 2007.
Изучение явления электромагнитной индукции
Автор Alexey На чтение 4 мин. Просмотров 1k. Опубликовано
Обновлено
Изучение возникновения электрического тока всегда волновало ученых. После того, как в начале XIX века датский ученый Эрстед выяснил, что вокруг электрического тока возникает магнитное поле, ученые задались вопросом: может ли магнитное поле порождать электрический ток и наоборот.Первым ученым, кому это удалось, был ученый Майкл Фарадей.
Опыты Фарадея
После многочисленных проведенных опытов Фарадей смог достичь кое-каких результатов.
1.Возникновение электрического тока
Для проведения опыта он взял катушку с большим количеством витков и присоединил ее к миллиамперметру (прибору, измеряющему силу тока). По направлению вверх и вниз ученый передвигал магнит по катушке.
Во время проведения эксперимента, в катушке действительно появлялся электрический ток по причине изменения магнитного поля вокруг нее.
По наблюдениям Фарадея стрелка миллиамперметра отклонялась и указывала на то, что движение магнита порождает собой электрический ток. При остановке магнита стрелка показывала нулевую разметку, т.е. ток не циркулировал по цепи.
рис. 1 Изменение силы тока в катушке за счет передвижения реjcтата
Данное явление, при котором ток возникает под действием переменного магнитного поля в проводнике, назвали явлением электромагнитной индукции.
2.Изменение направления индукционного тока
В своих последующих исследованиях Майкл Фарадей пытался выяснить, что влияет на направление возникающего индукционного электрического тока. Проводя опыты, он заметил, что изменяя числа мотков на катушке или полярность магнитов, направление электрического тока, которое возникает в замкнутой сети меняется.
Проводя опыты, он заметил, что изменяя числа мотков на катушке или полярность магнитов, направление электрического тока, которое возникает в замкнутой сети меняется.
3.Явление электромагнитной индукции
Для проведения опыта ученый взял две катушки, которые расположил близко друг к другу. Первая катушка, имеющая большое количество витков проволоки, была подсоединена к источнику тока и ключу, замыкающему и размыкающему цепь. Вторую такую же катушку он присоединил к миллиамперметру уже без подключения к источнику тока.
Проводя эксперимент, Фарадей заметил, что при замыкании электрической цепи возникает индуцированный ток, что видно по движению стрелки миллиамперметра. При размыкании цепи миллиамперметр также показывал, что в цепи есть электрический ток, но показания были прямо противоположными. Когда же цепь была замкнута и равномерно циркулировала ток, тока в электрической цепи согласно данным миллиамперметра не было.
https://youtu.be/iVYEeX5mTJ8
Вывод из экспериментов
В результате открытия Фарадея была доказана следующая гипотеза: электрический ток появляется только при изменении магнитного поля. Также было доказано, что изменение числа витков в катушке изменяет значение силы тока (увеличение мотков увеличивает силу тока). Причем индуцированный электрический ток может появиться в замкнутой цепи только при наличии переменного магнитного поля.
Также было доказано, что изменение числа витков в катушке изменяет значение силы тока (увеличение мотков увеличивает силу тока). Причем индуцированный электрический ток может появиться в замкнутой цепи только при наличии переменного магнитного поля.
От чего зависит индукционный электрический ток?
Основываясь на всем вышесказанном, можно отметить, что даже если есть магнитное поле, это не приведет к возникновению электрического тока, если данное поле не будет при этом переменным.
Так от чего же зависит величина индукционного поля?
- Число витков на катушке;
- Скорость изменения магнитного поля;
- Скорость движения магнита.
Магнитный поток является величиной, которая характеризует магнитное поле. Изменяясь, магнитный поток приводит к изменению индуцированного электрического тока.
рис.2 Изменение силы тока при перемещении а) катушки , в котором находится соленоид; б) постоянного магнита , внесением его в катушку
Закон Фарадея
Основываясь на проведенных опытах, Майкл Фарадей сформулировал закон электромагнитной индукции. Закон заключается в том, что, магнитное поле при своем изменении приводит к возникновению электрического тока, Ток же указывает на наличие электродвижущей силы электромагнитной индукции (ЭДС).
Закон заключается в том, что, магнитное поле при своем изменении приводит к возникновению электрического тока, Ток же указывает на наличие электродвижущей силы электромагнитной индукции (ЭДС).
Скорость магнитного тока изменяясь влечет за собой изменение скорости тока и ЭДС.
Закон Фарадея: ЭДС электромагнитной индукции равна численно и противоположна по знаку скорости изменения магнитного потока, который проходит через поверхность, ограниченную контуром
Индуктивность контура. Самоиндукция.
Магнитное поле создается в том случае, когда ток протекает в замкнутом контуре. Сила тока при этом влияет на магнитный поток и индуцирует ЭДС.
Самоиндукция – явление, при котором ЭДС индукции возникает при изменении силы тока в контуре.
Самоиндукция изменяется в зависимости от особенностей формы контура, его размеров и среды, его содержащей.
При увеличении электрического тока, ток самоиндукции контура может замедлить его. При его уменьшении, ток самоиндукции, напротив, не дает ему так быстро убывать. Таким образом, контур начинает обладать своей электрической инертностью, замедляющей любое изменение тока.
Таким образом, контур начинает обладать своей электрической инертностью, замедляющей любое изменение тока.
Применение индуцированного ЭДС
Явление электромагнитной индукции имеет применение на практике в генераторах, трансформаторах и двигателях, работающих на электричестве.
При этом ток для этих целей получают следующими способами:
- Изменение тока в катушке;
- Движение магнитного поля через постоянные магниты и электромагниты;
- Вращение витков или катушек в постоянном магнитном поле.
Открытие электромагнитной индукции Майкла Фарадея внесло большой вклад в науку и в нашу обыденную жизнь. Это открытие послужило толчком для дальнейших открытий в области изучения электромагнитных полей и имеет широкое применение в современной жизни людей.
Эксперимент по закону индукции Фарадея — EX-5541 — Продукты
Краткое описание продукта
В катушке, качающейся в магнитном поле, индуцируется напряжение. Исследуются закон Фарадея и закон Ленца, и энергия, рассеиваемая в нагрузочном резисторе, сравнивается с потерей энергии маятника катушки.
Жесткий маятник с катушкой на конце качается через подковообразный магнит. Резистивная нагрузка подключается к катушке, а наведенное напряжение регистрируется с помощью датчика напряжения.Угол измеряется с помощью датчика вращательного движения, который также действует как ось маятника. Наведенное напряжение отображается в зависимости от времени и угла. Мощность, рассеиваемая на резисторе, рассчитывается по напряжению, а энергия, преобразованная в тепловую энергию, определяется путем нахождения площади под кривой зависимости мощности от времени. Эта энергия сравнивается с потерей энергии, определяемой по амплитуде и скорости маятника.
Эта энергия сравнивается с потерей энергии, определяемой по амплитуде и скорости маятника.
Закон Фарадея используется для оценки магнитного поля магнита по максимальному индуцированному напряжению.Кроме того, направление индуцированного напряжения, когда катушка входит и выходит из магнитного поля, исследуется и анализируется с использованием закона Ленца.
PASCO Advantage: PASCO Capstone™ рассчитывает энергию и мощность, используя данные о напряжении и угле. Наведенное напряжение и расчеты отображаются в режиме реального времени, когда катушка проходит через магнит.
Концепции
- Магнитный поток
- Закон индукции Фарадея
- Закон Ленца
- Сохранение энергии
- Электроэнергия
Что 0 Включено 15
Требуется программное обеспечение
Для этого продукта требуется программное обеспечение PASCO для сбора и анализа данных.Мы рекомендуем следующие варианты. Для получения дополнительной информации о том, какое программное обеспечение подходит для вашего класса, см. раздел Сравнение программного обеспечения: SPARKvue и Capstone »
раздел Сравнение программного обеспечения: SPARKvue и Capstone »
Требуется интерфейс
Для подключения этого продукта к вашему компьютеру или устройству требуется интерфейс PASCO. Мы рекомендуем следующие варианты. Подробную информацию о функциях, возможностях и дополнительных параметрах см. в нашем Руководстве по сравнению интерфейсов »
Physics | Бесплатный полнотекстовый | Закон Фарадея и магнитная индукция: причина и следствие, эксперимент и теория
1.Введение
Майкл Фарадей был первым, кто опубликовал экспериментальные результаты по электромагнитной индукции, явлению, которое часто описывается как индуцируемый ток при изменении магнитного потока через проводящую катушку.
Это явление компактно описывается математической моделью, связывающей «электродвижущую силу» (ЭДС) V вокруг замкнутой цепи с временными изменениями магнитного потока Φ — интеграла магнитного поля по поверхности, очерченной этим замыканием.Закон индукции Фарадея можно напрямую связать с векторным уравнением Максвелла–Фарадея ([1], с. 160). Используя обозначения, где ∂t≡d/dt, уравнения записываются как
160). Используя обозначения, где ∂t≡d/dt, уравнения записываются как
V=-∂tΦ↔∇×E=-∂tB,
(1)
где E — электрическое поле, а B — магнитное поле. Однако фундаментальный закон причинности требует, чтобы следствия не могли возникнуть раньше их причин; и это ожидание имеет математические последствия. Эти следствия порождают, в частности, знаменитые соотношения Крамерса-Кронига [2,3,4], которые можно использовать для ограничения как спектральных свойств физических величин, так и моделей, используемых для их описания.Здесь мы принимаем локальный взгляд на причинность, а не глобальный, и используем временную область, наиболее естественную для выражения причинного поведения. В этом случае существует схема [5] приписывания определенных причинно-следственных ролей компонентам математических моделей, основанная на дифференциальных уравнениях во времени (подробности см. также в [6,7]). Проще говоря, это означает, что в любой уравнение математической модели это член производной по времени высшего порядка, который следует рассматривать как следствие, а остальные члены как причины; но обратите внимание, что его также можно применять к системам связанных уравнений (например,ж. , уравнения Максвелла ([5], раздел V), а также далее в этой статье в разделе 5.2). В качестве простого примера, поскольку второй закон Ньютона можно записать в виде ∂tv=F/m, то согласно [5] мы можем утверждать, что сила F вызывает изменение скорости v массы m. Использование этой интерпретации особенно естественно при рассмотрении численного решения динамических физических моделей; см. Приложение A в [8], где основное внимание уделяется тому, что происходит при обновлении текущего состояния системы [9,10] (т.т. е., интегрированные вперед во времени), или по мере того, как вселенная расширяется в свое «будущее» (как, например, в подходе причинного множества [11]). Обратите внимание, что другие обсуждения и подходы к причинности в электродинамике, относящиеся к закону Фарадея существуют [12,13,14]. В частности, одна значительная школа мысли предпочитает связывать все обратно с первоначальными исходными терминами (см., например, [12] и примечания в Приложении B к [8]). К сожалению, поскольку закон Фарадея не содержит явных ссылок на исходные заряды, мы не можем анализировать его в отношении причины и следствия на этой основе — нам потребовалась бы другая модель, которая ссылалась бы на исходные заряды и их движение (т.
, уравнения Максвелла ([5], раздел V), а также далее в этой статье в разделе 5.2). В качестве простого примера, поскольку второй закон Ньютона можно записать в виде ∂tv=F/m, то согласно [5] мы можем утверждать, что сила F вызывает изменение скорости v массы m. Использование этой интерпретации особенно естественно при рассмотрении численного решения динамических физических моделей; см. Приложение A в [8], где основное внимание уделяется тому, что происходит при обновлении текущего состояния системы [9,10] (т.т. е., интегрированные вперед во времени), или по мере того, как вселенная расширяется в свое «будущее» (как, например, в подходе причинного множества [11]). Обратите внимание, что другие обсуждения и подходы к причинности в электродинамике, относящиеся к закону Фарадея существуют [12,13,14]. В частности, одна значительная школа мысли предпочитает связывать все обратно с первоначальными исходными терминами (см., например, [12] и примечания в Приложении B к [8]). К сожалению, поскольку закон Фарадея не содержит явных ссылок на исходные заряды, мы не можем анализировать его в отношении причины и следствия на этой основе — нам потребовалась бы другая модель, которая ссылалась бы на исходные заряды и их движение (т. g., см. [15]). Следовательно, в дальнейшем мы решили использовать только локальное и совместимое с Крамерсом-Кронигом определение [5] для того, что составляет причинную интерпретацию математической модели. Используя локальный взгляд на причинность, описанный в [ 5] и во вставке 1, поскольку уравнение (1) не имеет производных по времени, применяемых к V, но одна производная по времени применяется к Φ, это означает, что ЭДС V следует рассматривать как причину, где изменение потока ∂tΦ является ее следствием . Как следствие, было бы более интуитивно переписать уравнение (1) как
g., см. [15]). Следовательно, в дальнейшем мы решили использовать только локальное и совместимое с Крамерсом-Кронигом определение [5] для того, что составляет причинную интерпретацию математической модели. Используя локальный взгляд на причинность, описанный в [ 5] и во вставке 1, поскольку уравнение (1) не имеет производных по времени, применяемых к V, но одна производная по времени применяется к Φ, это означает, что ЭДС V следует рассматривать как причину, где изменение потока ∂tΦ является ее следствием . Как следствие, было бы более интуитивно переписать уравнение (1) как
∂tΦ=−V↔∂tB=−∇×E,
(2)
где мы также вынуждены описывать пространственные градиенты электрического поля ∇×E как причину, а результирующие временные изменения поля B как его следствие.Несколько тревожно то, что теперь это означает, что мы не можем интерпретировать нашу математическую модель закона индукции Фарадея как наше предпочтительное причинно-следственное утверждение: то есть, где изменения в потоке индуцируют ЭДС (и, следовательно, управляют токами) [16,17,18]. Однако, основываясь на нашей математической модели, мы по-прежнему можем сделать более слабое утверждение, когда они просто приравниваются или связаны друг с другом [19]. Эта ситуация предполагает, что уравнение (2), несмотря на его полезность, просто не является хорошим. каузальное представление эксперимента, который мы имели в виду.Чтобы решить эту проблему, нам нужно провести четкое различие между причинностью, очевидной в эксперименте, и причинной интерпретацией математической модели, которая обязательно является лишь приближением к этому эксперименту. Хотя обычно мы надеемся, что они совпадают, кажется, что в случае закона Фарадея это не так, и в разделе 2 мы обсуждаем, почему (или как) это может быть.
Однако, основываясь на нашей математической модели, мы по-прежнему можем сделать более слабое утверждение, когда они просто приравниваются или связаны друг с другом [19]. Эта ситуация предполагает, что уравнение (2), несмотря на его полезность, просто не является хорошим. каузальное представление эксперимента, который мы имели в виду.Чтобы решить эту проблему, нам нужно провести четкое различие между причинностью, очевидной в эксперименте, и причинной интерпретацией математической модели, которая обязательно является лишь приближением к этому эксперименту. Хотя обычно мы надеемся, что они совпадают, кажется, что в случае закона Фарадея это не так, и в разделе 2 мы обсуждаем, почему (или как) это может быть.
Очевидно, было бы желательно, чтобы наше математическое описание индукции явно показывало, как ЭДС или электрический ток могут генерироваться в проводнике, будь то за счет изменяющихся свойств магнитного поля или за счет движения проводника в этих полях.В дальнейшем мы попробуем три (нерелятивистских) подхода к поиску математической модели, которая описывает, как некоторое свойство или поведение магнитного потока (или, возможно, только магнитного поля) явно приписывается как причина ЭДС.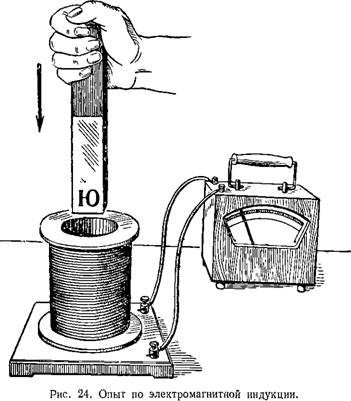
Первый, в разделе 3, основан на уравнении Максвелла-Фарадея и не работает. Второй, в разделе 4, вместо этого основан на уравнении Максвелла-Ампера и достигает этой важной цели, но, возможно, не очень удовлетворительным образом. Третий, в разделе 5, основан на законе силы Лоренца, и мы пробуем как простой абстрактный расчет, так и конкретную установку, распространенную на многих курсах бакалавриата, и выводим модель тока, вызванного магнитными полями и движением.Наконец, в разделе 6 мы делаем вывод.
Вставка 1. Как быть причинным: Рассмотрим простое модельное уравнение ∂tR(t)=Q(t), которое в используемой здесь интерпретации интерпретируется как «Q вызывает изменения в R». Используя математическое определение производной, в некоторый произвольный момент времени t0 уравнение модели имеет вид
limδ→0R(t0+δ)−R(t0−δ)2δ=Q(t0).
(3)
Непосредственно перед тем, как перейти к пределу, и для некоторого достаточно малого значения δ мы имеем
R(t0+δ)−R(t0−δ)2δ=Q(t0).
(4)
Теперь давайте попробуем использовать это как предсказатель будущего.Мы сразу видим, что самая последняя (или наиболее близкая к будущему) величина равна R(t0+δ), поэтому мы переставляем ее слева и получаем
R(t0+δ)=R(t0−δ)+2δQ(t0).
(5)
Здесь мы видим, что для обновления наших знаний о R до его следующего значения в момент t+δ требуется (а) прошлое знание R (т. е. R(t0−δ)) и (б) текущее знание Q (т. е. Q( т0)). Таким образом, ясно, что значение Q вызывает изменения в R. Если бы вместо этого мы захотели вычислить Q, надеясь сказать что-то вроде «R вызывает Q», мы бы сначала преобразовали уравнение (4) в форму
Q(t0)=R(t0+δ)−R(t0−δ)2δ,
(6)
но сразу увидим, что Q(t0) зависит от будущего значения R, а именно R(t0+δ) – а зависимость от будущих значений несовместима со стандартными представлениями о причинности.
В этой презентации на уровне бакалавриата, посвященной магнитной индукции, подчеркивается различие между любой предполагаемой экспериментальной причинностью и причинностью, закодированной в ее математической модели.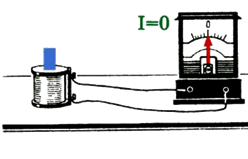 Это показывает, что очевидно полезное определение ЭДС на самом деле работает против наших попыток создать модель, в которой оно индуцируется изменениями магнитного потока. Напротив, альтернативный подход к электрическим токам, генерируемым движением и/или изменением магнитного поля, не имеет таких ограничений.
Это показывает, что очевидно полезное определение ЭДС на самом деле работает против наших попыток создать модель, в которой оно индуцируется изменениями магнитного потока. Напротив, альтернативный подход к электрическим токам, генерируемым движением и/или изменением магнитного поля, не имеет таких ограничений.
2.Эксперимент
Рассмотрим пример эксперимента, состоящего из двух частей устройства: (i) магнита и (ii) петли или катушки с прикрепленным вольтметром, как показано на рисунке 1. Когда мы перемещаем магнит вблизи петли, мы видим индуцированное напряжение. Поэтому на основе этого экспериментального опыта вполне естественно — и действительно точно — сделать вывод, что движение магнита вызывало появление напряжения (или ЭДС). Если мы также изучаем физику, мы могли бы также связать движение магнита с величиной магнитного потока, пересекающего петлю, и, таким образом, сказать, что наш эксперимент показывает, что «изменение потока вызывает ЭДС».Только что описанная «экспериментальная причинность» не вызывает сомнений. Однако здесь исследуется объединение этого экспериментального опыта причинности с любой причинной интерпретацией математического выражения закона Фарадея, то есть уравнения (2).
Однако здесь исследуется объединение этого экспериментального опыта причинности с любой причинной интерпретацией математического выражения закона Фарадея, то есть уравнения (2).
Для лучшего понимания нам нужно начать с более ясного понимания того, почему мы можем сделать вывод, что напряжение было вызвано нашими действиями по перемещению магнита. Примечательно, что мы должны понимать, что это происходит не только потому, что мы видели конечное напряжение, зарегистрированное на вольтметре, так как оно могло быть просто плохо обнулено и всегда иметь какое-то конечное значение или компенсировано эффектами какого-то внешнего поля, не относящегося к индукционному эксперименту. .Вместо этого мы говорим «вызвано», потому что после того, как (и когда) мы переместили магнит рядом с петлей, напряжение, регистрируемое вольтметром, изменилось. Изменение напряжения — это видимый эффект, который заставляет нас искать его причину. По крайней мере, мы должны хотеть, чтобы наша каузальная модель индукции описывала, как происходят изменения напряжения («ЭДС») из-за внешних раздражителей.
Давайте теперь попробуем математически систематизировать наш эксперимент, принимая во внимание предварительно определенный вход (движение магнита), и при этом искать результирующий эффект на выходе (ЭДС V).Предполагая для простоты магнит фиксированной силы с одинаково фиксированной ориентацией, единственным входом в нашу модель должна быть только его скорость v(t). Это v(t) есть причина; это то, что мы указываем в плане эксперимента, а затем реализуем. Мы надеемся или ожидаем, что эта причина приведет к изменению. Это изменение должно быть видно как влияние на измеряемую ЭДС, так что в один момент она может быть равна нулю, а в следующий момент уже будет другой, т. ).Таким образом, мы могли бы написать
где L() — функция или оператор, содержащий всю необходимую информацию об электромагнетизме, структуре поля, создаваемого магнитом, законе силы Лоренца для зарядов и теории цепей. Теперь мы можем с первого взгляда увидеть, что структура математическая модель Уравнение (7) для нашего эксперимента не имеет той же формы, что и закон Фарадея: уравнение (2) явно относится только к изменениям потока ∂tΦ, а не к изменениям ЭДС. На самом деле, это не должно вызывать удивления, поскольку уравнение (2) даже не является попыткой микроскопической модели экспериментального процесса, когда движущийся магнит создает изменяющееся распределение электромагнитного поля, которое затем влияет на движение электронов. производить или изменять электрические токи (т.g., [15]), и, таким образом, в последующем возникает ЭДС. Поскольку в уравнении (2) опущено так много экспериментальных подробностей, на первый взгляд неясно, почему мы должны ожидать, что они вообще совпадают, не говоря уже об идеальном совпадении.
На самом деле, это не должно вызывать удивления, поскольку уравнение (2) даже не является попыткой микроскопической модели экспериментального процесса, когда движущийся магнит создает изменяющееся распределение электромагнитного поля, которое затем влияет на движение электронов. производить или изменять электрические токи (т.g., [15]), и, таким образом, в последующем возникает ЭДС. Поскольку в уравнении (2) опущено так много экспериментальных подробностей, на первый взгляд неясно, почему мы должны ожидать, что они вообще совпадают, не говоря уже об идеальном совпадении.
Тем не менее, в дальнейшем мы попытаемся найти фарадеевский закон, который лучше соответствует нашей экспериментальной концепции.
3. Уравнение Максвелла–Фарадея
Сначала рассмотрим стандартный вывод закона индукции Фарадея, начиная с уравнения Максвелла для ротора; обратите внимание, однако, что некоторые подходы используют обратный подход и начинают с индукции и сводят ее к уравнению завитка.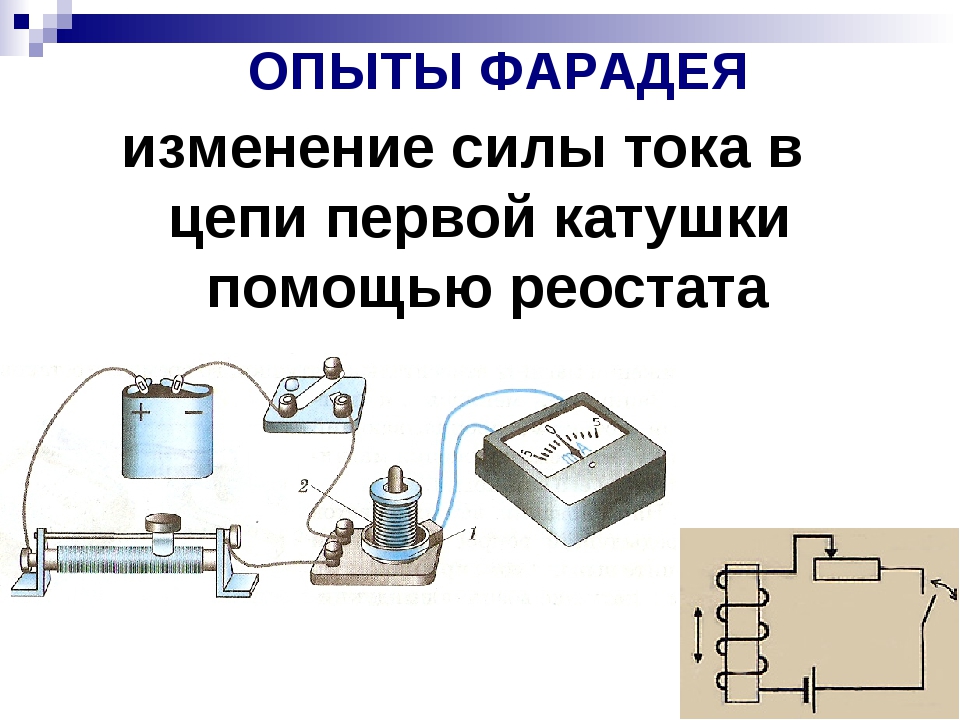
Мы начинаем с петли материала и рассматриваем эту петлю как границу C некоторой замкнутой поверхности S, и рассматриваем электрическое поле E и магнитное поле B, как показано на рисунке 2. Вывод продолжается, начиная с уравнения Максвелла-Фарадея. , взяв поверхностный интеграл с обеих сторон, а затем применив теорему Стокса к левой части (lhs), чтобы преобразовать поверхностный интеграл по S в линейный интеграл по элементам dl вдоль C:
∫SdS·∂tB=-∫SdS·∇×E,
(9)
∂t∫SdS·B=−∮Cdl·E,
(10)
Причинная интерпретация этого уравнения должна заключаться [5] в том, что ЭДС «вызывает» изменения в потоке Φ — на самом деле мы не можем принять общепринятую интерпретацию, согласно которой изменения в потоке индуцируют (или вызывают) ЭДС.Обратите внимание, что это не интерпретация экспериментальных фактов или наблюдений, а интерпретация, основанная на математической модели. Далее, обратите внимание, что ЭДС, т.е. провода, вычисляется не так, как мы, возможно, могли бы ожидать, т. е. следуя одиночному заряду на его пути вокруг проводящей петли, чтобы вычислить пройденную разность напряжений. Вместо этого мы рассмотрели силы, действующие на непрерывную линию бесконечно малых зарядов на петле в один момент, и проинтегрировали эти силы.Без модели движения этих зарядов то, что мы смоделировали, больше похоже на диэлектрическое кольцо со связанными зарядами и токами, привязанными к своим местам, а не на проводящую проволочную петлю со свободно движущимися зарядами и токами [20]. Конечно. , с практической точки зрения закон индукции Фарадея, полученный выше и показанный в уравнении (1), является чрезвычайно полезным выражением, и он совместим с экспериментальными измерениями. Примечательно, что в электродвигателе или генераторе скорость вращения оси дает нам собственную угловую частоту ω, так что производная потока по времени становится простым умножением на ω; и далее, в таком квазистационарном случае атрибуция причинности становится несущественной.Однако его полезность не является гарантией того, что он предоставит математическую модель, инкапсулирующую случайные свойства, на которые мы могли бы надеяться для генерации ЭМП.
е. следуя одиночному заряду на его пути вокруг проводящей петли, чтобы вычислить пройденную разность напряжений. Вместо этого мы рассмотрели силы, действующие на непрерывную линию бесконечно малых зарядов на петле в один момент, и проинтегрировали эти силы.Без модели движения этих зарядов то, что мы смоделировали, больше похоже на диэлектрическое кольцо со связанными зарядами и токами, привязанными к своим местам, а не на проводящую проволочную петлю со свободно движущимися зарядами и токами [20]. Конечно. , с практической точки зрения закон индукции Фарадея, полученный выше и показанный в уравнении (1), является чрезвычайно полезным выражением, и он совместим с экспериментальными измерениями. Примечательно, что в электродвигателе или генераторе скорость вращения оси дает нам собственную угловую частоту ω, так что производная потока по времени становится простым умножением на ω; и далее, в таком квазистационарном случае атрибуция причинности становится несущественной.Однако его полезность не является гарантией того, что он предоставит математическую модель, инкапсулирующую случайные свойства, на которые мы могли бы надеяться для генерации ЭМП. Тем не менее, позже в разделе 5 мы увидим, что этой трудности нет при поиске моделей, демонстрирующих влияние на ток в результате изменений магнитного поля или потока.
Тем не менее, позже в разделе 5 мы увидим, что этой трудности нет при поиске моделей, демонстрирующих влияние на ток в результате изменений магнитного поля или потока.
4. Уравнение Максвелла–Ампера
В разделе 3 мы видели, что уравнение Максвелла–Фарадея не дает желаемой причинной интерпретации. Следовательно, давайте попробуем альтернативный вывод для модели индукции, начиная с уравнения Максвелла для ротора, которое представляет закон Ампера.Цель здесь — показать, как некое подходящее свойство магнитного поля — возможно, связанное с магнитным потоком — явным образом вызывает изменение ЭДС. Это означало бы, что мы можем заняться генерацией ЭДС из ничего и использовать это, чтобы мотивировать появление индуцированного тока. Поскольку в предыдущем разделе мы видели, что, согласно [5], уравнение Максвелла-Фарадея неверно объясняет картину «магнитные поля, вызывающие (индуцирующие) ток», уравнение Максвелла-Ампера с его обратными ролями для электрических и магнитные вклады могут показаться более многообещающими. Снова возьмем петлю, содержащую заряды, с замкнутой поверхностью S и границей C, и рассмотрим поля электрического смещения и магнитной индукции D и H, как на рисунке 3. Вывод продолжается, начиная с уравнения Максвелла-Ампера, беря поверхностный интеграл обеих сторон, а затем применить теорему Стокса к правой части (правой части), чтобы преобразовать этот поверхностный интеграл в линейный интеграл:
Снова возьмем петлю, содержащую заряды, с замкнутой поверхностью S и границей C, и рассмотрим поля электрического смещения и магнитной индукции D и H, как на рисунке 3. Вывод продолжается, начиная с уравнения Максвелла-Ампера, беря поверхностный интеграл обеих сторон, а затем применить теорему Стокса к правой части (правой части), чтобы преобразовать этот поверхностный интеграл в линейный интеграл:
∫SdS·∂tD=∫SdS·∇×H−∫SdS·J,
(13)
ϵ∂t∫SdS·E=µ−1∮Cdl·B−∫SdS·J,
(14)
где J — электрический ток.Отсюда мы можем непосредственно видеть, что ни ЭДС, ни поток Φ не возникают. Однако некоторые дальнейшие размышления приведут нас к большему успеху, если взять завиток с обеих сторон перед применением поверхностного интеграла. Если ϵ — диэлектрическая проницаемость, а μ — проницаемость, мы имеем:
∇×∂tD=∇×∇×H−∇×J,
(15)
ϵ∫SdS·∇×∂tE=µ−1∫SdS·∇×∇×B−∫SdS·∇×J,
(16)
ϵ∂t∮Cdl·E=µ−1∫SdS·∇×∇×B−∮Cdl·J,
(17)
∂t∮Cdl·E=µϵ−1∫SdS·∇×∇×B−ϵ−1∮Cdl·J.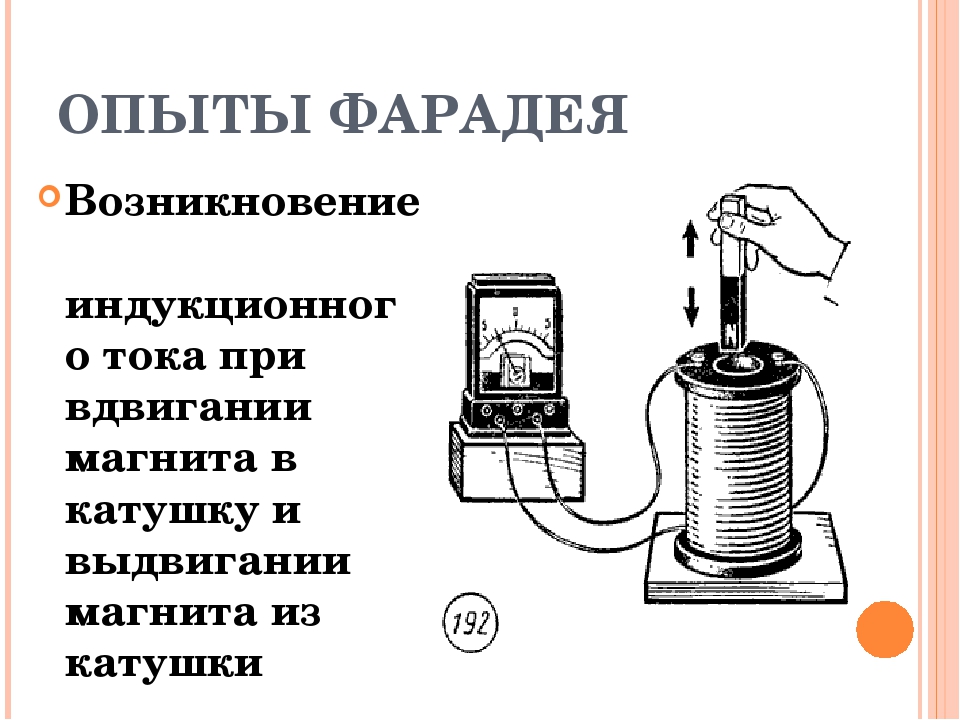
(18)
Это уравнение теперь дает нам ЭДС от левой стороны. линейный интеграл, рассчитанный так же, как в разделе 3. Поскольку ∇·B=0, а c=1/µϵ — скорость света, мы можем написать
∂tV=c2∫SdS·∇2B−ϵ−1∮Cdl·J.
(19)
Этот результат представляет собой уравнение, подобное индукции, которому мы можем дать четко определенную причинно-следственную интерпретацию того, где возникает ЭДС: поскольку пространственные вариации B (или, при интегрировании, пространственные вариации потока) вызывают изменения ЭДС, как и токи.
Хотя мы могли бы попытаться рассмотреть этот общий случай, поучительно упростить его и взять случай нулевого тока, когда все dS ориентированы по оси z, а B в основном выровнена по оси z и изменяется в направлении z, так что только ее компонента Bz является значительный. С учетом этих допущений и расчета эффективного магнитного потока как ΦA=SBz, т.е. после перемещения п.в.с. поверхностный интеграл через пространственные производные по оси z ∂z, мы можем написать упрощенное уравнение
∂tV=−c2∂z2SBz=−c2∂z2ΦA.
(20)
И последнее замечание: в ситуациях, когда разумно заменить c∂z на ∂t, мы также можем восстановить что-то эквивалентное обычной форме, но с дополнительной производной по времени с обеих сторон. Однако при этой замене поток ΦA снова подвергается производной по времени высшего порядка. Таким образом, индукционная модель также вернулась к той же каузальной интерпретации, противоположной нашему предпочитанию «потока как причины».
5. Закон силы Лоренца
Несмотря на относительно знакомый характер расчетов в разделах 3 и 4, во многих отношениях может показаться более естественным вывести модель индукции тока, начав с закона силы Лоренца.Поскольку закон магнитной индукции Фарадея не основан на эффектах, вызванных приложенными электрическими полями (см., например, [1], стр. 160), я начинаю с количества движения p электрического заряда q в чисто магнитном поле
Это сама по себе модель, в которой изменения импульса заряда вызываются (магнитной) силой Лоренца F. Хотя рассмотрение изменений импульса в контексте индуцированных токов необычно, в приведенных ниже расчетах это удобный способ суммирование задействованных сил.
Хотя рассмотрение изменений импульса в контексте индуцированных токов необычно, в приведенных ниже расчетах это удобный способ суммирование задействованных сил.
Как и в предыдущих расчетах, теперь мы надеемся найти полезным определение величины, подобной ЭДС. Однако в то время как в этих расчетах ЭДС была получена из линейного интеграла электрического поля, здесь мы вместо этого основываем ее на интеграле по движущимся зарядам; и чтобы подчеркнуть это различие, мы обозначаем его VL, а не просто V.
5.1. Простая петля
Здесь мы применим ее к (одному из) зарядов в нашей проводящей петле. Это более общая формулировка Блини и Блини ([1], с.160), но они используют его просто как поддержку чего-то эквивалентного стандартному расчету, сделанному в разделе 3. определяется как dW=F·dl с силой F вдоль линейного элемента dl,
Сначала мы линейно интегрируем по петле (контур C), содержащей заряды q и движущейся в v, чтобы получить полную ЭДС VL,
VL=q−1∮Cdl·F=∮Cdl·v×B.
(23)
Далее мы преобразуем правую сторону. линейный интеграл к поверхностному интегралу завитка по теореме Стокса
VL=q−1∮Cdl·F=∫SdS·∇×v×B,
(24)
так что теперь мы можем использовать стандартную векторную идентичность для ∇ × (A × B),
VL=∫SdS·v∇·B−B∇·v+B·∇v−v·∇B.
(25)
Первый член равен нулю, так как ∇·B=0; и мы можем еще больше упростить, удалив второй член, если поле скорости для зарядов (по сути, масштабированный ток) не имеет источников или стоков. Здесь для удобства мы пошли дальше и настаиваем на постоянном поле скоростей v, так что третий член также обращается в нуль. Результат
VL=−∫SdS·v·∇B.
(26)
Чтобы сделать этот результат более понятным, мы дополнительно упростим ситуацию, как показано на рисунке 4, рассматривая квадратную петлю в плоскости xy, которая ограничивает поверхность S, площадь которой S перпендикулярна оси z.Магнитное поле ориентировано вдоль оси z, так что единственная ненулевая составляющая — это Bz, и оно изменяется только вдоль оси x и с фиксированной скоростью. Затем мы перемещаем нашу петлю вбок параллельно оси x с фиксированной скоростью v, так что мы получаем прямое равенство, но без каких-либо производных по времени и, следовательно, без подразумеваемой причинно-следственной связи:
Затем мы перемещаем нашу петлю вбок параллельно оси x с фиксированной скоростью v, так что мы получаем прямое равенство, но без каких-либо производных по времени и, следовательно, без подразумеваемой причинно-следственной связи:
Это кажется наиболее тесно связанным с формулировкой Максвелла-Ампера в разделе 4, которая также зависит от пространственных градиентов B. Однако мы могли бы адаптировать это соотношение, преобразовав часть числителя dx скорости v=dx/dt и знаменатель dx часть градиента поля dBz/dx, чтобы получить
ВЛ=-SdxdtdBzdx→-SdBzdt,
(28)
что является нормальным выражением закона Фарадея, если предположить эквивалентность VL и V, несмотря на то, что они получены из разных исходных точек.Несмотря на это, нам все еще не удалось найти математическую модель с искомыми причинными свойствами, в которых свойства магнитного поля или его потока вызывают появление или изменение токов.
5.2. U-образный стержень и движущийся стержень
Давайте теперь попробуем добиться большего прогресса, рассматривая конкретную ситуацию, а не абстрактные конструкции. Рассмотрим стандартную систему в стиле бакалавриата: длинную прямоугольную проводящую U-образную форму в постоянном магнитном поле с проводящим стержнем, замыкающим токовую петлю, как показано на рисунке 5.Затем говорят, что стержень скользит по плечам буквы U, тем самым изменяя площадь, заключенную в петлю, и, следовательно, изменяя замкнутый поток. Тогда мы могли бы напрямую применить закон Фарадея из левой части. уравнения (1) и использовать скорость изменения потока для расчета ЭДС, а затем (если мы хотим) индукционного тока, связанного с этой ЭДС. Однако, учитывая наше решение настаивать на наличии конкретной причинной интерпретации, и поскольку закон Фарадея не соответствует этой интерпретации, мы должны поэтому выбрать другую математическую модель.Поскольку без предположения о пространственных градиентах поля, которые не являются необходимым свойством нашего примера, мы не можем использовать выражение, основанное на амперах, в уравнении (19), мы начнем с закона силы. Однако использование уравнения закона силы Лоренца (21) означает, что мы можем сразу увидеть, что здесь есть две силы, действующие на заряды: в магнитном поле.
Рассмотрим стандартную систему в стиле бакалавриата: длинную прямоугольную проводящую U-образную форму в постоянном магнитном поле с проводящим стержнем, замыкающим токовую петлю, как показано на рисунке 5.Затем говорят, что стержень скользит по плечам буквы U, тем самым изменяя площадь, заключенную в петлю, и, следовательно, изменяя замкнутый поток. Тогда мы могли бы напрямую применить закон Фарадея из левой части. уравнения (1) и использовать скорость изменения потока для расчета ЭДС, а затем (если мы хотим) индукционного тока, связанного с этой ЭДС. Однако, учитывая наше решение настаивать на наличии конкретной причинной интерпретации, и поскольку закон Фарадея не соответствует этой интерпретации, мы должны поэтому выбрать другую математическую модель.Поскольку без предположения о пространственных градиентах поля, которые не являются необходимым свойством нашего примера, мы не можем использовать выражение, основанное на амперах, в уравнении (19), мы начнем с закона силы. Однако использование уравнения закона силы Лоренца (21) означает, что мы можем сразу увидеть, что здесь есть две силы, действующие на заряды: в магнитном поле.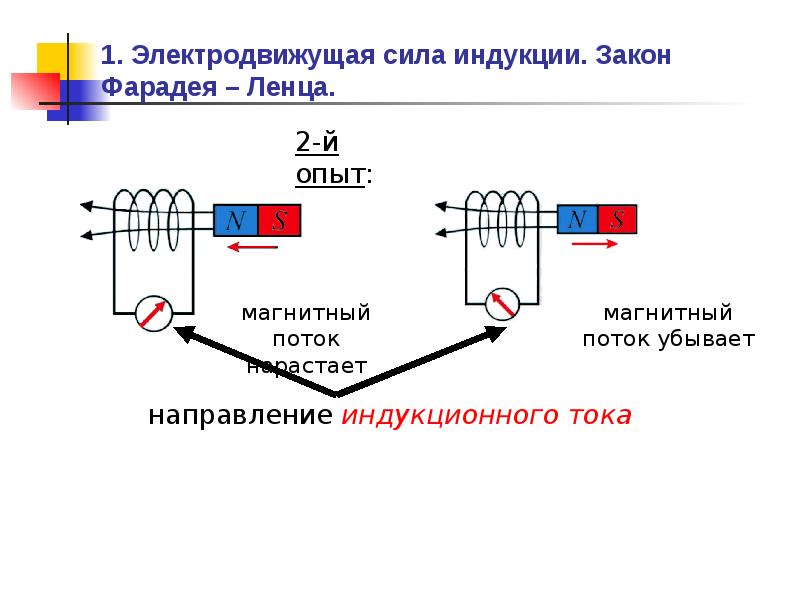 Эта сила направлена вдоль стержня, изменяя скорость заряда в стержне, а затем распространяясь на всю петлю.
Эта сила направлена вдоль стержня, изменяя скорость заряда в стержне, а затем распространяясь на всю петлю.
Во-вторых, на заряды в стержне действует магнитная сила из-за движения этих зарядов вдоль стержня в магнитном поле. Эта сила толкает заряды перпендикулярно стержню, что может быть связано с эффектом Холла. Здесь мы предполагаем, что этот эффект Холла быстро поляризует стержень в масштабе времени, намного более быстром, чем другие процессы, так что суммарный эффект проявляется только в остаточной замедляющей силе самого стержня.
Это означает, что мы можем использовать закон силы, чтобы вычислить (а) как ток J в петле реагирует на скорость v стержня, и (б) как движение стержня реагирует на ток J в петле .Естественно, это будут динамические уравнения с явной причинностью.
Здесь мы принимаем провод U фиксированным и жестким, так что любые силы, действующие на него из-за протекания по нему тока и/или наличия электромагнитных полей, не учитываются. Сама проволока U имеет сколь угодно длинные плечи с расстоянием между ними и длиной основания Lbar, каждое с линейной плотностью заряда σ. Стержень имеет массу M и скорость v, что дает импульс Pbar. Он установлен перпендикулярно плечам проволоки U на расстоянии L от их основания и (также) имеет плотность заряда σ и длину Lbar.
Стержень имеет массу M и скорость v, что дает импульс Pbar. Он установлен перпендикулярно плечам проволоки U на расстоянии L от их основания и (также) имеет плотность заряда σ и длину Lbar.
Ток J состоит из потока зарядов с поступательным импульсом Pcur. Он имеет полный заряд Q, но только q=Lbarσ в стержне, который является единственной частью, на которую действует магнитная сила. Если (эффективная) массовая плотность зарядов [21] равна ρ, скорость зарядов вдоль стержня равна u, а их скорость равна u=Pcur/ρLtot(t), где Ltot(t)=2Lbar+2L(t ). Предполагается, что углы U и контакты между U и стержнем отводят (например, за счет упругого отражения) заряды вокруг петли (т.т. е. в их новом направлении), так что Pcur движется либо вперед (по часовой стрелке на рис. 5), либо назад (против часовой стрелки) вокруг петли; плотность заряда тока также предполагается фиксированной [22]. Полная сила, действующая на стержень, обусловлена только магнитной силой, которую необходимо просуммировать по длине Lbar. Обратите внимание, что поле внутри петли здесь не имеет значения, важна его напряженность в каждой точке стержня в момент интегрирования общей силы. Плотность силы на каждом элементе стержня равна
Обратите внимание, что поле внутри петли здесь не имеет значения, важна его напряженность в каждой точке стержня в момент интегрирования общей силы. Плотность силы на каждом элементе стержня равна
так что в сумме получаем
∂tPbar=LbarσPcurBz/ρLtot(t).
(30)
Суммарная сила тока представляет собой не только магнитную силу, которую необходимо просуммировать по длине стержня Lbar, но также включает линейный резистивный член γ(t), где γ(t)=rLtot(t), а r пропорционально к сопротивлению на единицу длины. Обратите внимание, что (опять же) поле внутри петли здесь не важно, важна его сила вдоль стержня в его текущем местоположении. Поскольку скорость стержня по проводам равна Pbar/M, плотность силы на каждом элементе тока равна
∂tpcur=-σv∇B-rpcur,
(31)
так что в сумме имеем
∂tPcur=-LbarσPbarBz/M-γ(t)Pcur.
(32)
Это два линейных связанных дифференциальных уравнения, и их проще всего объединить, взяв производную по времени от уравнения Pcur и подставив одно в другое.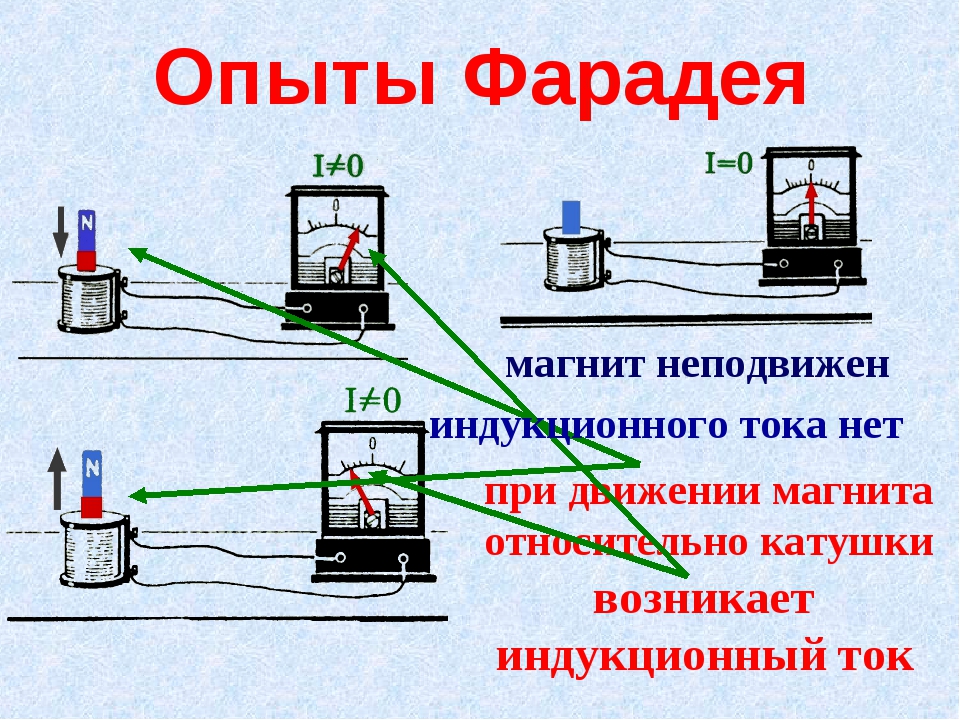 Упрощая уравнения, не отображая явных зависимостей Ltot(t) и γ(t) от времени, получаем
Упрощая уравнения, не отображая явных зависимостей Ltot(t) и γ(t) от времени, получаем
∂t2Pcur=-LbarσBz/M∂tPbar-∂tγPcur+-LbarσPbar/M∂tBz
(33)
=-LbarσBz/MLbarσPcurBz/ρLtot-∂tγ(t)Pcur-LbarσPbar/M∂tBz
(34)
=-Lbar2σ2Bz2MρLtotPcur-∂tγPcur-LbarσPbar/M∂tBz
(35)
=-Ω2Pcur-∂tγPcur-σLbarPbar/M∂tBz
(36)
=-Ω2Pcur-∂tγPcur-σLbarv∂tBz,
(37)
где
Ω(t)=LbarσBzρMLtot(t).
(38)
Заметим, что мы не можем напрямую заменить Pcur на ток J в дифференциальных уравнениях, так как они связаны через общую длину проводника Ltot(t). Кроме того, управляющий член, зависящий от ∂tBz, пропорционален v(t)=Pbar(t)/M, что имеет свою динамику: если магнитное поле меняется во времени, недостаточно пытаться решить только уравнение ( 37), нам также необходимо рассмотреть уравнение (30).
Поскольку в этом результате содержится несколько сложных взаимозависимостей, мы теперь рассмотрим некоторые поучительные частные случаи.
5.2.1. Постоянное магнитное поле
Рассмотрим случай, когда магнитное поле постоянно во времени и во всем пространстве, так что ∂tBz=0, т. е. третья правая в.с. член уравнения (37) обращается в нуль. Здесь стержень после первоначального толчка будет колебаться вперед и назад в соответствии с частотным параметром Ω(t), но амплитуда этих колебаний затухает со скоростью, определяемой γ(t). Мы также можем видеть что при небольших вариациях L(t) и Ltot(t) параметр частоты будет фактически постоянным и, таким образом, станет истинной частотой колебаний.В этом режиме мы можем прямо заменить Pcur на ток J=σPcur/ρLtot и получить
∂t2J=−Ω2J−∂tγJ.
(39)
Это привело бы к затухающим синусоидальным колебаниям тока и, следовательно, к связанным с ними колебаниям скорости стержня; поскольку ускорение стержня можно связать с током уравнением (30).
5.2.2. Изменяющееся во времени магнитное поле
. Уравнение (37) сохранило возможность зависимости Bz от времени. Мы можем видеть, что изменение поля ∂tBz действует на ускорение тока, но способом, зависящим от Pbar (т.е., скорость стержня). Таким образом, ток по-прежнему хочет колебаться, хотя это вряд ли будет простой синусоидой, при этом изменения поля действуют как управляющий фактор. Обратите внимание, что причинно-следственная связь сохраняется, поскольку влияние на Pcur имеет второй порядок по времени, на один порядок больше, чем что на Bz [5,23].
Мы можем видеть, что изменение поля ∂tBz действует на ускорение тока, но способом, зависящим от Pbar (т.е., скорость стержня). Таким образом, ток по-прежнему хочет колебаться, хотя это вряд ли будет простой синусоидой, при этом изменения поля действуют как управляющий фактор. Обратите внимание, что причинно-следственная связь сохраняется, поскольку влияние на Pcur имеет второй порядок по времени, на один порядок больше, чем что на Bz [5,23].
5.2.3. Электродвижущая сила
. Теперь мы можем рассмотреть, что говорит нам уравнение (37) об ЭДС, индуцированной в петле; поскольку то, что мы делаем, основано на законе силы Лоренца, мы используем ЭДС VL, а не обычный закон Фарадея V.Поскольку VL — это работа на единицу заряда, или линейный (петлевой) интеграл силы, а сила — это просто изменение количества движения, мы имеем, что VL = σ−1∂tPcur. Это означает, что для небольших изменений Ltot(t) мы можем практически повторно использовать уравнение (37) напрямую — мы просто применяем другую производную по времени и заменяем Pcur, чтобы получить
∂t2VL=−Ω2VL−∂tγVL−∂tLbarv∂tBz.
(40)
На первый взгляд может показаться, что уравнение показывает временные изменения магнитного поля, вызывающие изменения в ЭДС.Конечно, поскольку оно содержит больше деталей, зависящих от модели, следует ожидать некоторых отличий от стандартного закона Фарадея в уравнении (2) или альтернативного закона Ампера в уравнении (19). прямой результат преобразования Pcur в VL теперь имеет производную по времени второго порядка, действующую на B, точно так же, как левая часть, действующая на VL. Поскольку они имеют одинаковые порядки производной по времени, они имеют один и тот же причинный статус — при правильном сочетании их можно интерпретировать как результат действия других членов уравнения (40), т.е.т. е. причиноподобные термины VL и ∂tγVL, а также термины, включающие v. Это означает, что уравнение (40) не имеет причинной интерпретации, которую мы искали, например, такой, где временные изменения первого порядка в магнитном поле вызывали изменения второго порядка в ЭДС.
5.
 3. Обсуждение
3. Обсуждение
Здесь мы увидели, что оба наших расчета, основанные на силовом законе, т. е. очень простая и более реалистичная система, не дают нам результата, в котором можно было бы сказать, что свойства магнитного поля вызывают изменения в магнитном поле. ЭДС.Тем не менее причинно-следственные связи, подобные той, к которой мы стремились, все же можно сделать, не ссылаясь на ЭДС, а вместо этого используя утверждения о том, что (изменения) свойств магнитного поля вызывают токи.
6. Выводы
В этой статье мы попытались найти версию или новый вывод закона Фарадея, математическая форма которого имитирует причинно-следственную интерпретацию, которую мы хотели бы иметь, а именно изменения магнитного потока через петлю вызывают изменения ЭДС вокруг эта петля.Однако обычная математическая форма закона Фарадея несовместима с этим желанием и позволяет лишь сказать, что ЭДС вызывает изменение потока.
Чтобы устранить этот очевидный недостаток, мы вывели фарадеевский закон, основанный на уравнении максвелловского завихрения Ампера, что действительно позволило нам говорить об индуцированных изменениях ЭДС, но вместо этого они были вызваны пространственными градиентами магнитного потока, которые не совсем то, на что мы надеялись.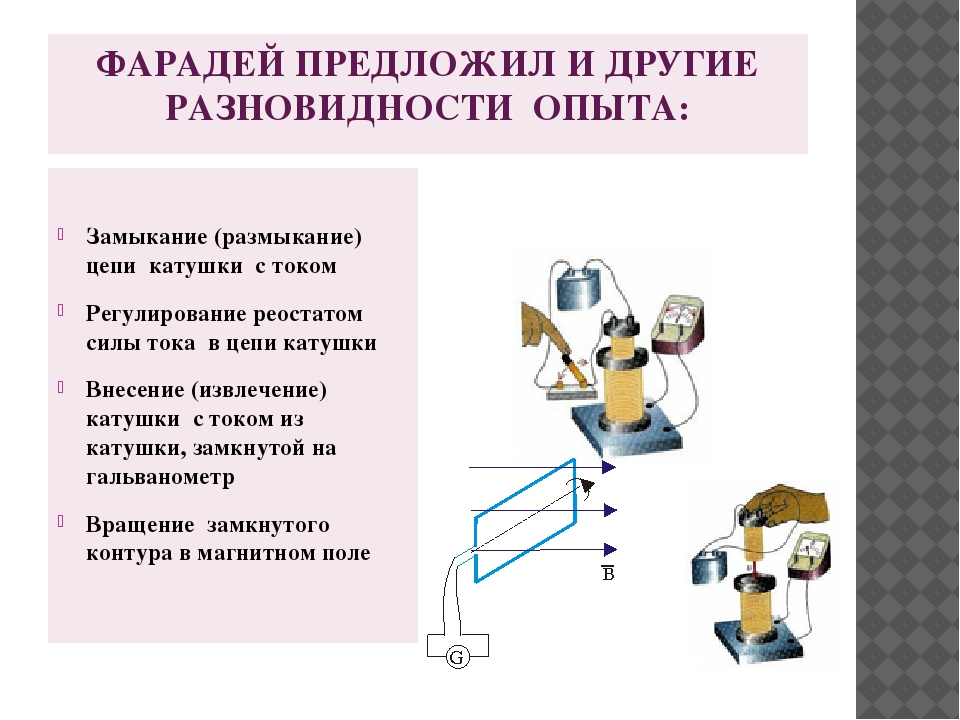 Это побудило нас попробовать альтернативный подход, основанный на законе силы Лоренца, микроскопические основы которого показали многообещающие свойства магнитного поля, действительно индуцирующие (вызывающие) изменения тока, как в абстрактной, так и в более реалистичной обстановке.Однако, когда математическая модель была преобразована, чтобы ссылаться вместо этого на индуцированные изменения в величине VL, подобной ЭДС, мы обнаружили, что модель стала несовместимой с желаемой причинной интерпретацией, подчеркнув, что именно настойчивое использование ЭДС вносит трудности.
Это побудило нас попробовать альтернативный подход, основанный на законе силы Лоренца, микроскопические основы которого показали многообещающие свойства магнитного поля, действительно индуцирующие (вызывающие) изменения тока, как в абстрактной, так и в более реалистичной обстановке.Однако, когда математическая модель была преобразована, чтобы ссылаться вместо этого на индуцированные изменения в величине VL, подобной ЭДС, мы обнаружили, что модель стала несовместимой с желаемой причинной интерпретацией, подчеркнув, что именно настойчивое использование ЭДС вносит трудности.
Таким образом, наше исследование показало, что следует быть осторожным при интерпретации причинно-следственных связей процессов магнитной индукции и опасаться зависимости от скрытых или неявных допущений, которые могут привести к вводящим в заблуждение выводам.Во-первых, следует четко различать интерпретации, относящиеся к эксперименту, и интерпретации, относящиеся к математической модели; различие, которое жизненно важно в случае закона Фарадея. Во-вторых, поскольку самое близкое к понятию «изменения магнитного потока, индуцирующего ЭДС», которое мы можем подобрать, основано на уравнении Максвелла-Ампера, а не Максвелла Фарадея, нам нужно быть осторожными при выборе причинно-следственной интерпретации эмпирических законов, выведенных из эксперимента или совместимых с ним.
Во-вторых, поскольку самое близкое к понятию «изменения магнитного потока, индуцирующего ЭДС», которое мы можем подобрать, основано на уравнении Максвелла-Ампера, а не Максвелла Фарадея, нам нужно быть осторожными при выборе причинно-следственной интерпретации эмпирических законов, выведенных из эксперимента или совместимых с ним.
Physics4Kids.com: Электричество и магнетизм: Закон Фарадея
Закон индукции Фарадея является одним из важных понятий электричества.В нем рассматривается, как изменение магнитных полей может вызвать протекание тока в проводах. По сути, это формула/понятие, описывающее, как создается разность потенциалов ( разность напряжений ) и в какой степени. Это огромная концепция, чтобы понять, что изменение магнитного поля может создать напряжение.
Майкл Фарадей был английским физиком, работавшим в начале 1800-х годов. Он работал с другим ученым по имени сэром Хамфри Дэви . Большое открытие Фарадея произошло в 1831 году, когда он обнаружил, что при изменении магнитного поля можно создать электрический ток.Он много работал с электричеством, например, делал генераторы и экспериментировал с электрохимией и электролизом.
Большое открытие Фарадея произошло в 1831 году, когда он обнаружил, что при изменении магнитного поля можно создать электрический ток.Он много работал с электричеством, например, делал генераторы и экспериментировал с электрохимией и электролизом.
Эксперименты Фарадея начались с магнитных полей, которые оставались неизменными. Эта установка не индуцировала ток . Только когда он начал изменять магнитные поля, ток и напряжение были индуцированы (созданны). Он обнаружил, что изменения магнитного поля и размера поля связаны с величиной создаваемого тока. Ученые также используют термин магнитный поток .Магнитный поток — это величина, равная силе магнитного поля, умноженной на площадь поверхности устройства.
Вам придется пересмотреть свои греческие буквы, когда вы запомните настоящую формулу. Вот основы…
E=дБ/дт
«E» — это значение индуцированного напряжения (старое название напряжения было «Электродвижущая сила» или ЭДС.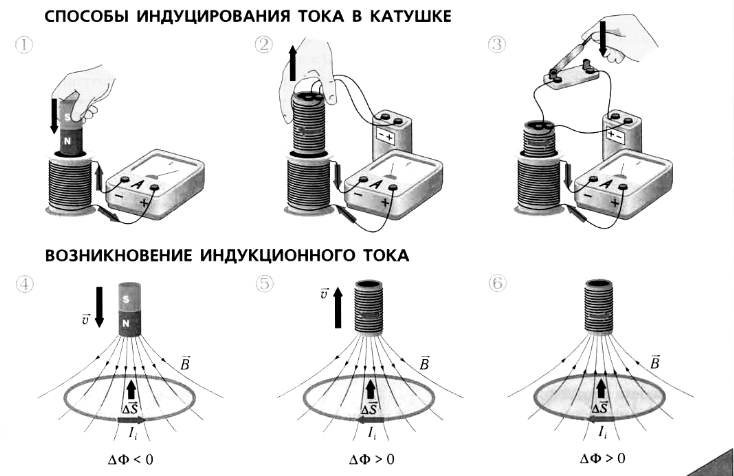 Это буква «E» в уравнении). Изменение времени для эксперимента «dt». Время измеряется в секундах. Наконец, «дБ» означает изменение магнитного потока.Магнитный поток представляет собой силовые линии магнитного поля. Поток равен BA, где B — напряженность магнитного поля, а A — площадь. Эта формула немного сложнее, чем те, которые вы, возможно, видели раньше.
Это буква «E» в уравнении). Изменение времени для эксперимента «dt». Время измеряется в секундах. Наконец, «дБ» означает изменение магнитного потока.Магнитный поток представляет собой силовые линии магнитного поля. Поток равен BA, где B — напряженность магнитного поля, а A — площадь. Эта формула немного сложнее, чем те, которые вы, возможно, видели раньше.
По-английски: величина создаваемого напряжения равна изменению магнитного потока, деленному на изменение во времени. Чем больше изменение магнитного поля, тем больше напряжение.
Или поищите на сайтах по конкретной теме.
Радиоволны и электричество (видео NASA SciFiles)
Encyclopedia.com:
http://www.encyclopedia.com/topic/Faradays_law.aspx
Википедия (электромагнитная индукция):
http://en. wikipedia.org/wiki/Электромагнитная_индукция 2 Британская энциклопедия (Закон индукции Фарадея):
wikipedia.org/wiki/Электромагнитная_индукция 2 Британская энциклопедия (Закон индукции Фарадея):
hhttp://www.britannica.com/EBchecked/topic/201744/Закон индукции Фарадея
Секции Physics4Kids
Сеть научных и математических сайтов Rader
Наведенный ток > Лаборатория поддержки лекций по физике и астрономии > USC Дана и Дэвид Дорнсайф Колледж литературы, искусств и наук
EM.2(1) — Эксперимент Фарадея по электромагнитной индукции
В этой демонстрации используются индукционная катушка и лекционный гальванометр. Стержневой магнит, погруженный в катушку, создает в катушке электрический ток, который показывает гальванометр. Когда магнит удаляется, возникает ток в противоположном направлении. Отклонение стрелки гальванометра хорошо видно всему классу.
Отклонение стрелки гальванометра хорошо видно всему классу.
Эксперимент Фарадея теперь проводится с одной петлей вместо катушки с проволокой.Прогиб в гальванометре в этом случае значительно меньше. Также это можно сделать с увеличением количества петель, чтобы показать его зависимость от количества петель.
Топ
EM.2(2) — Индукционные рельсы
К лекционному гальванометру подключены две токопроводящие шины. Рельсы размещены вокруг магнитного поля большого подковообразного магнита. Когда проводящий стержень быстро скользит по рельсам, разрезая магнитное поле, индуцируется ЭДС.ЭДС индукции определяется отклонением стрелки гальванометра. Переместите стержень в противоположном направлении, и стрелка гальванометра отклонится в противоположном направлении. Индуцированный ток имеет такое направление, чтобы создать магнитный поток, противодействующий изменению магнитного поля, вызванному скольжением проводника.
Топ
EM.2(3) — Катушки с токовой связью
Две индукционные катушки соединены длинными проводами и установлены далеко друг от друга в аудитории.Вплотную к ним располагают высокие стойки, так что в них колеблются стержневые магниты на пружинах. Когда один магнит начинает колебаться, индуцированный ток заставляет колебаться и другой.
Топ
EM.2(4) — Наведенный ток — две катушки
Одна индукционная катушка подключается к лекционным гальванометрам, как в ЕМ.2(2), а другая к источнику постоянного тока и выключателю. Одна катушка установлена поверх другой, но они не соединены.Включите питание. Когда переключатель разомкнут или замкнут, ток, индуцируемый в другой катушке, будет показан на гальванометре.
Железный сердечник, продетый через обе катушки, усилит эффект.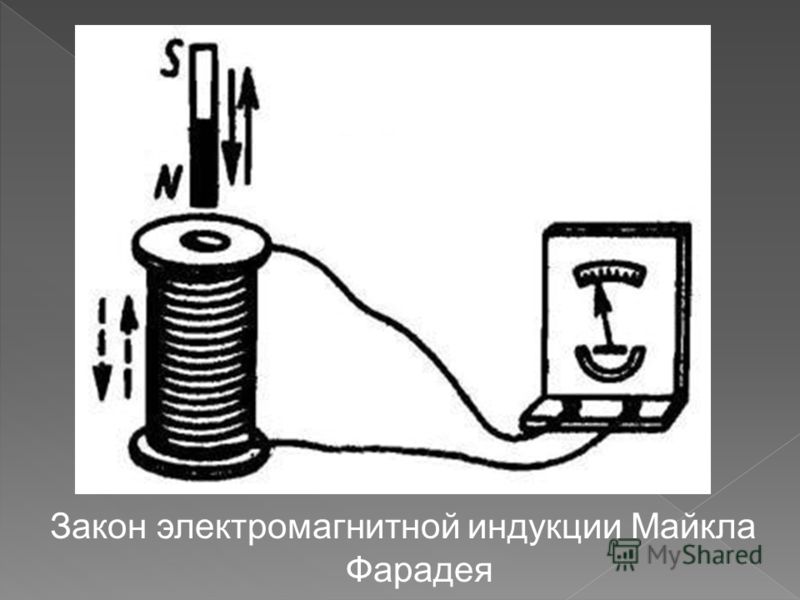
Топ
EM.2(5) — эксперимент с прыгающим кольцом
Индукционная катушка с удлиненным железным сердечником установлена вертикально, часть железного сердечника выдвинута вверх. Сплошное металлическое кольцо установлено вокруг железного сердечника над катушкой.Индукционная катушка подключена к источнику переменного тока. Когда на катушку подается переменный ток, металлическое кольцо подбрасывается вверх в воздух. Попробуй с разрезным кольцом и ничего не получится.
Ток, индуцируемый в металлическом кольце, создает магнитное поле, противодействующее полю, создаваемому индукционной катушкой.
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Топ
ЕМ.2(6) — Погружная лампа
Используется та же установка, что и в EM.2(5), но теперь с опущенным железным сердечником, чтобы стакан можно было поместить поверх катушки. Внутри стакана есть небольшая катушка проволоки с маленькой лампой посередине. При воздействии на индукционную катушку переменной ЭДС загорается лампочка. Наполните стакан водой, и он снова загорится под действием переменного ЭДС.
Внутри стакана есть небольшая катушка проволоки с маленькой лампой посередине. При воздействии на индукционную катушку переменной ЭДС загорается лампочка. Наполните стакан водой, и он снова загорится под действием переменного ЭДС.
Топ
ЕМ.2(7) — Магнитный фонарик
Встряхивание этого фонарика в течение 1 минуты дает 1-2 часа света. Он имеет две катушки внутри, которые хорошо видны наблюдателям. Эта демонстрация демонстрирует принципы закона Ленца.
Верх
EM.2(8) — электромагнитное демпфирование
Индукционная катушка кладется на бок и поддерживается так, чтобы железный сердечник располагался горизонтально.Железный сердечник может выступать примерно на половину своей длины из катушки. Опорный стержень, прикрепленный к торцевой пластине индукционной катушки, удерживает медное или алюминиевое кольцо над сердечником магнита с помощью шнура. Кольцо свободно висит на сердечнике. Катушка подключается к аккумулятору 6 В или к источнику постоянного тока через переключатель. Быстро замкните переключатель. Кольцо будет внезапно выброшено наружу, а затем медленно вернется в вертикальное положение без колебаний. Разомкните переключатель, и кольцо сначала повернется к катушке, а затем начнет колебаться вокруг своего свободного положения.
Кольцо свободно висит на сердечнике. Катушка подключается к аккумулятору 6 В или к источнику постоянного тока через переключатель. Быстро замкните переключатель. Кольцо будет внезапно выброшено наружу, а затем медленно вернется в вертикальное положение без колебаний. Разомкните переключатель, и кольцо сначала повернется к катушке, а затем начнет колебаться вокруг своего свободного положения.
Когда переключатель замкнут, ток, наведенный в кольце, создает противодействующее поле, которое, взаимодействуя с полем, создаваемым током в индукционной катушке, замедляет движение кольца. Энергия, поступающая от движения кольца, поглощается индуцированным током в кольце, что обеспечивает превосходную демонстрацию электромагнитного демпфирования. Когда переключатель разомкнут, магнитное поле практически отсутствует, и демпфирование не происходит.
Генератор с ручным приводом, подключенный к электрической лампочке, также является полезной демонстрацией закона Ленца, поскольку доброволец может проверить, что его намного легче крутить, когда в цепи нет нагрузки, т. е.е. когда лампочка отключена.
е.е. когда лампочка отключена.
Топ
EM.2(9) — Индукционная искровая катушка
Этот эксперимент демонстрирует электромагнитную индукцию: повторяющиеся прерывания первичного тока индуцируют импульсы высокого напряжения на вторичных клеммах. Это визуально наблюдается по возникающим искрам между этими выводами (расположенными сверху аппарата с индукционной катушкой). Аппарат подключен к источнику питания постоянного тока (напряжение ~7В, ток ~2А).
Включите аппарат, убедившись, что вибратор расположен вдали от основного терминала. Медленно поворачивайте ручку, чтобы переместить вибратор к терминалу, пока первый не начнет вибрировать и искры не начнут прыгать по вторичным терминалам.
Топ
EM.2(10) — индукционная трубка
Целью этого эксперимента является демонстрация реализации индукционного тока. Трубка примерно три фута с равномерно расположенными, плотно связанными катушками подключена к усилителю.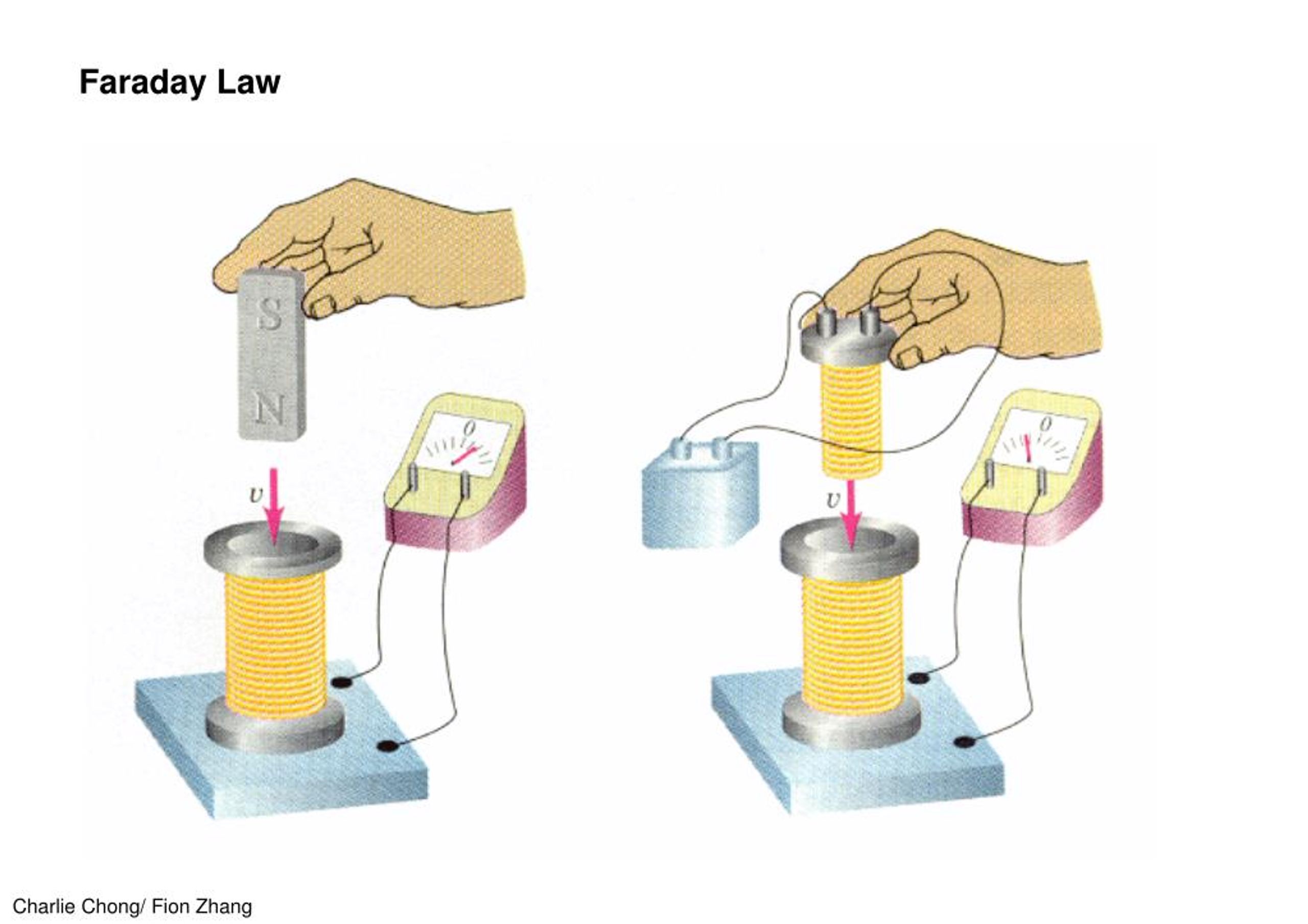 Каждый набор катушек соединяется с предыдущим набором, в конечном итоге сходясь к месту соединения выводов. Наведенный ток, собранный с катушек, направляется от места подключения проводов к усилителю, где сигнал проявляется на слух через три пятидюймовых динамика. Сигнал может быть довольно слабым, поэтому рекомендуется установить усилитель на максимальную громкость.
Каждый набор катушек соединяется с предыдущим набором, в конечном итоге сходясь к месту соединения выводов. Наведенный ток, собранный с катушек, направляется от места подключения проводов к усилителю, где сигнал проявляется на слух через три пятидюймовых динамика. Сигнал может быть довольно слабым, поэтому рекомендуется установить усилитель на максимальную громкость.
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Топ
ЕМ.2(11) — Индукционная петля
Цель этого эксперимента — показать, что напряжение (а значит, и ток) будет индуцироваться вокруг петли, когда магнитный поток, проходящий через петлю, изменяется со временем. Величина индуцированного напряжения зависит от числа витков в петле проводника. В этом эксперименте есть три варианта. Чтобы увидеть изменение наведенного напряжения, мы будем использовать проекционный измеритель. Чтобы максимизировать отклонение вольтметра, используйте для перемещения петли руку, а не встроенный двигатель. (ПРИМЕЧАНИЕ: индуцированное напряжение вызывает небольшое отклонение вольтметра, чтобы произвести впечатление на студента, вы можете переключиться в текущий режим, который максимизирует отклонение проекционного измерителя).
(ПРИМЕЧАНИЕ: индуцированное напряжение вызывает небольшое отклонение вольтметра, чтобы произвести впечатление на студента, вы можете переключиться в текущий режим, который максимизирует отклонение проекционного измерителя).
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Топ
EM.2(12) — Радиоприемник с двойной катушкой
В этом эксперименте с использованием двух наборов плотно намотанных катушек показано, как ток/напряжение может передаваться от приемника к динамику с помощью магнитной индукции.Установка состоит из ресивера, подключенного к DVD-плееру, который обеспечивает передачу музыки. Приемник подключен к одному набору катушек, набору А, который обеспечивает зависящее от времени магнитное поле, необходимое для возникновения магнитной индукции. Второй набор катушек, набор B, подключен к пятидюймовому динамику, на который будет захватываться выходной сигнал DVD-плеера. По мере того, как наборы A и B приближаются друг к другу, магнитный поток в наборе B будет увеличиваться, тем самым увеличивая силу выходного сигнала, громкость.Изменение выходного сигнала в зависимости от расстояния между наборами A и B можно анализировать вместе с эффектом вращения. Относительное вращение между наборами A и B изменит выходную силу таким образом, что при 90 градусах магнитный поток в наборе B будет равен нулю, то есть выходной сигнал отсутствует.
По мере того, как наборы A и B приближаются друг к другу, магнитный поток в наборе B будет увеличиваться, тем самым увеличивая силу выходного сигнала, громкость.Изменение выходного сигнала в зависимости от расстояния между наборами A и B можно анализировать вместе с эффектом вращения. Относительное вращение между наборами A и B изменит выходную силу таким образом, что при 90 градусах магнитный поток в наборе B будет равен нулю, то есть выходной сигнал отсутствует.
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Верх
EM.2(13) — динамик в бумажном стаканчике
Динамик — это устройство, преобразующее электронный сигнал в звук.В этой демонстрации электронный сигнал преобразуется в переменный ток и проходит по проводу от источника сигнала. Проволочная петля с током индуцирует магнитное поле, перпендикулярное проволочной петле. Это маленькое магнитное поле взаимодействует с большим магнитным полем, создаваемым при вставке большого постоянного магнита в чашку динамика.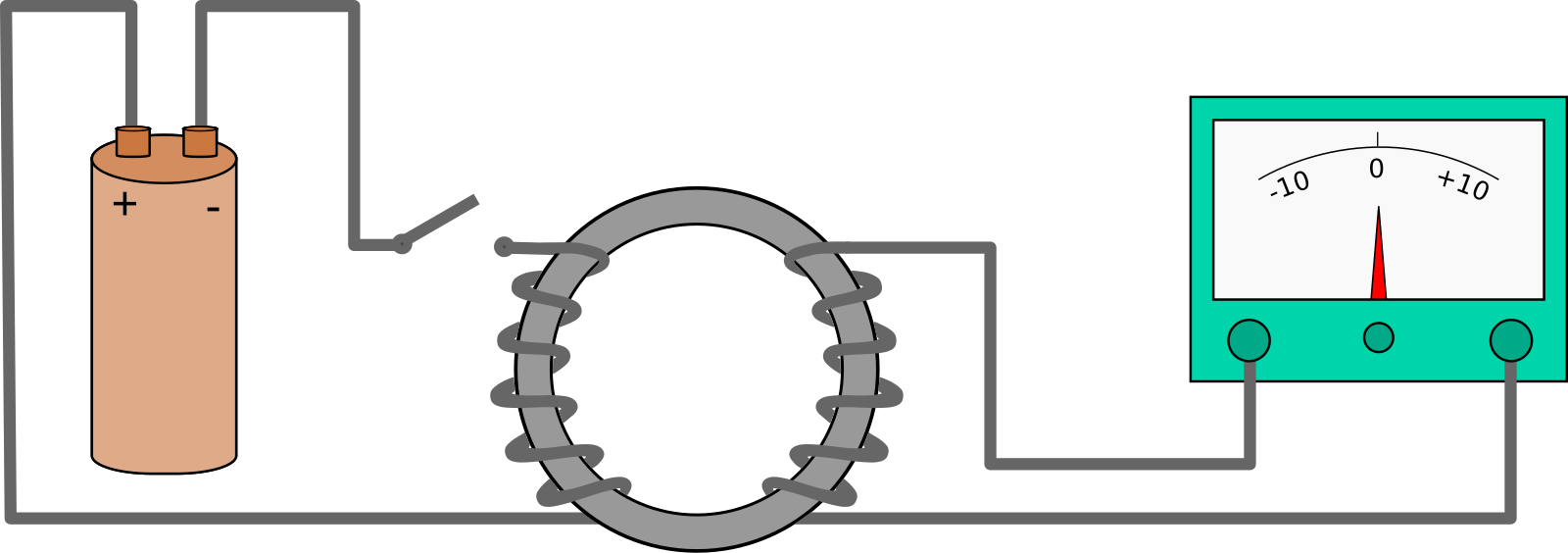 Магнитный поток создает в среде возмущение, колебания, которые и порождают звук, который мы слышим благодаря наличию воздуха.
Магнитный поток создает в среде возмущение, колебания, которые и порождают звук, который мы слышим благодаря наличию воздуха.
Нажмите здесь, чтобы посмотреть видео этой демонстрации.
Top
Эксперименты Фарадея по электромагнитной индукции
Эксперименты Фарадея по электромагнитной индукции
Первый Эксперимент
Рассмотрим закрытый
цепь, состоящая из катушки C из изолированного провода и гальванометра G
как показано на рисунке 4.2 (а). Гальванометр не показывает отклонения, т.к.
в цепи нет электрического тока.
Когда стержневой магнит
вставленный в стационарную катушку северным полюсом к катушке,
представляет собой мгновенное отклонение гальванометра.Это свидетельствует о том, что электрический
в катушке устанавливается ток (рис. 4.2(б)). Если магнит остается неподвижным
внутри катушки гальванометр не показывает прогиба (рис. 4.2, в).
Стержневой магнит теперь
снятый с катушки, гальванометр снова дает мгновенное отклонение
но в обратном направлении. Таким образом, электрический ток течет в противоположном направлении.
Таким образом, электрический ток течет в противоположном направлении.
направлении (рис. 4.2(г)). Теперь, если магнит двигается быстрее, он дает большее
отклонение из-за большего тока в цепи (рис. 4.2(д))
Стержневой магнит
наоборот, то есть южный полюс теперь обращен к катушке. Когда описанный выше эксперимент
повторяются, отклонения противоположны полученным в случае северного
столб (рис. 4.2(е)).
Если магнит сохраняется
стационарно, а катушка перемещается к катушке или от нее, аналогичные результаты
получаются. Делается вывод, что всякий раз, когда существует относительное движение между
катушки и магнита, в гальванометре есть отклонение, указывающее
установка электрического тока в катушке.
Второй эксперимент
Рассмотрим два закрытых
цепи, как показано на рисунке 4.3 (а). Схема, состоящая из катушки Р ,
батарея B и ключ K называются первичной цепью, а
цепь с катушкой S и гальванометром G называется вторичной
схема. Катушки P и S находятся в состоянии покоя в непосредственной близости.
Катушки P и S находятся в состоянии покоя в непосредственной близости.
по отношению друг к другу.
Если первичный контур
замыкается, в первичной цепи начинает течь электрический ток. При этом
время гальванометр дает мгновенное отклонение (рис. 4.3, а)).
После этого, когда
электрический ток достигает определенного установившегося значения, отклонения в
гальванометр.
Аналогично, если основной
цепь размыкается, электрический ток начинает уменьшаться и снова возникает
внезапное отклонение, но в противоположном направлении (рис. 4.3(б)). Когда
электрический ток становится равным нулю, гальванометр не показывает отклонения.
Из вышеперечисленного
наблюдений, делается вывод, что всякий раз, когда электрический ток в первичной
цепь меняется, гальванометр показывает отклонение.
Закон Фарадея
Электромагнитная индукция
По результатам его
опытов, Фарадей понял, что
всякий раз, когда магнитный
поток, связанный с замкнутой катушкой, изменяется, индуцируется ЭДС (электродвижущая сила)
и, следовательно, в цепи течет электрический ток. Этот ток называется
Этот ток называется
индукционный ток, а ЭДС, вызывающая этот ток, называется индуктивной
э.д.с. Это явление известно как электромагнитная индукция.
Основываясь на этой идее,
Опыты Фарадея понимаются следующим образом. Во-первых
Эксперимент, когда стержневой магнит помещается близко к катушке, часть магнитного поля
силовые линии стержневого магнита проходят через катушку, т. е. магнитный поток равен
связан с катушкой.Когда стержневой магнит и катушка приближаются друг к другу,
магнитный поток, связанный с катушкой, увеличивается. Таким образом, это увеличение магнитного потока
индуцирует ЭДС, и, следовательно, переходный электрический ток течет в цепи в одном направлении (рис. 4.4 (а)).
В то же время, когда
они удаляются друг от друга, магнитный поток связан с катушкой
уменьшается. Уменьшение магнитного потока снова индуцирует ЭДС, противоположную
направлении и, следовательно, электрический ток течет в противоположном направлении (рис.
4.4(б)). Таким образом, в гальванометре происходит отклонение, когда есть относительное движение между катушкой и стержнем.
магнит.
Во втором
Эксперимент, когда по первичной обмотке P протекает электрический ток,
вокруг нее создается магнитное поле. Магнитные линии этого поля проходят
через себя и соседнюю вторичную катушку S .
Когда первичный контур
открыт, в нем не течет электрический ток и, следовательно, магнитный поток связан
со вторичной обмоткой равен нулю (рис. 4.5(а)).
Однако, когда
первичная цепь замкнута, увеличивающийся ток создает магнитное поле
вокруг первичной катушки. Поэтому магнитный поток, связанный со вторичным
катушка увеличивается. Этот увеличивающийся связанный поток индуцирует переходный электрический ток.
ток во вторичной обмотке (рис. 4.5(б)). Когда электрический ток в
первичной обмотке достигает устойчивого значения, магнитный поток, связанный с
вторичной обмотке не изменяется, а электрический ток во вторичной обмотке
исчезнет.
Аналогично, когда
первичная цепь разорвана, уменьшающийся первичный ток вызывает электрический разряд.
ток во вторичной обмотке, но в обратном направлении (рис. 4.5(в)).
Таким образом, гальванометр отклоняется всякий раз, когда изменяется
первичный ток.
Выводы
Эксперименты Фарадея сформулированы как два закона.
Первый закон
Всякий раз, когда магнитный поток
связанные с замкнутой цепью, изменяются, в цепи индуцируется ЭДС.
Второй закон
Величина индуцированного
ЭДС в замкнутом контуре равна скорости изменения магнитного потока во времени
связана с цепью.
Если магнитный поток
связанный с катушкой изменяется на dΦ B за время dt , тогда
ЭДС индукции равна
.
Знак минус в
приведенное выше уравнение дает направление индуцированного тока, который будет иметь дело
в следующем разделе. Если катушка, состоящая из N витков, намотана туго
Если катушка, состоящая из N витков, намотана туго
что каждый виток покрывает одну и ту же площадь, то поток через каждый виток будет
то же. Тогда полная ЭДС, индуцируемая в катушке, равна
.
Здесь, NΦ B
называется потокосцеплением, определяемым как произведение числа витков Н на
катушка и магнитный поток, связывающий каждый виток катушки Φ B .
ПРИМЕР 4.3
А
цилиндрический стержневой магнит удерживается вдоль оси круглого соленоида. Если
магнит вращается вокруг своей оси, выяснить, есть ли электрический ток
наводится в катушке.
Раствор
магнитное поле цилиндрического магнита симметрично относительно его оси. Как
магнит вращается вдоль оси соленоида, индукционный ток отсутствует
в соленоиде, потому что поток, связанный с соленоидом, не изменяется из-за
к вращению магнита.
ПРИМЕР 4. 4
4
А закрытый
катушка из 40 витков площадью 200 см 2 , вращается в магнитном поле
плотностью потока 2 Вб·м -2 . Он вращается из положения, когда его плоскость
составляет угол 30º с
поле в положение, перпендикулярное полю, за время 0,2 сек. Найди
величина ЭДС, наводимой в катушке вследствие ее вращения.
Раствор
Н = 40 витков; В = 2 Вб·м -2
A = 200 см 2 = 200 ´ 10 -4 м 2 ;
ПРИМЕР 4.5
А
Прямой токопроводящий провод сбрасывают горизонтально с определенной высоты
протяженность с востока на запад. Будет ли в нем индуцироваться ЭДС? Обоснуйте свой
отвечать.
Раствор
Да! Ан
ЭДС будет индуцироваться в проводе, потому что он движется перпендикулярно
горизонтальная составляющая магнитного поля Земли.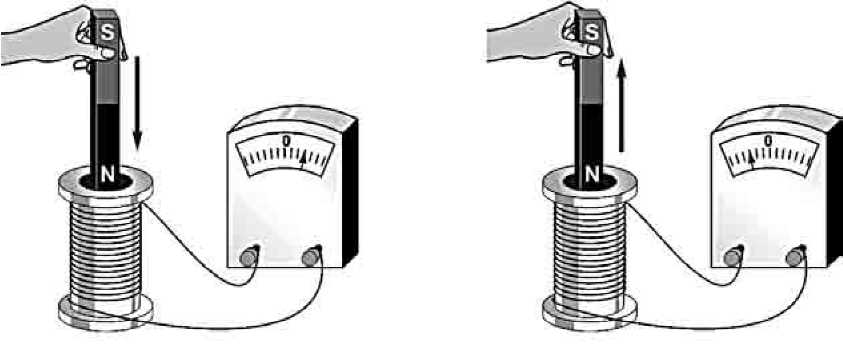
6.2 Закон индукции Фарадея: Закон Ленца
Применение электромагнитной индукции
Существует множество применений закона индукции Фарадея, которые мы рассмотрим в этой и других главах. На этом этапе давайте упомянем несколько, которые связаны с хранением данных и магнитными полями. Очень важное применение связано с аудио- и видеозаписями на лентах . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, на которое намотана катушка проволоки — электромагнит (рис. 6.8). Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы, которые являются функцией амплитуды и частоты сигнала, создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, что приводит к записи сигнала.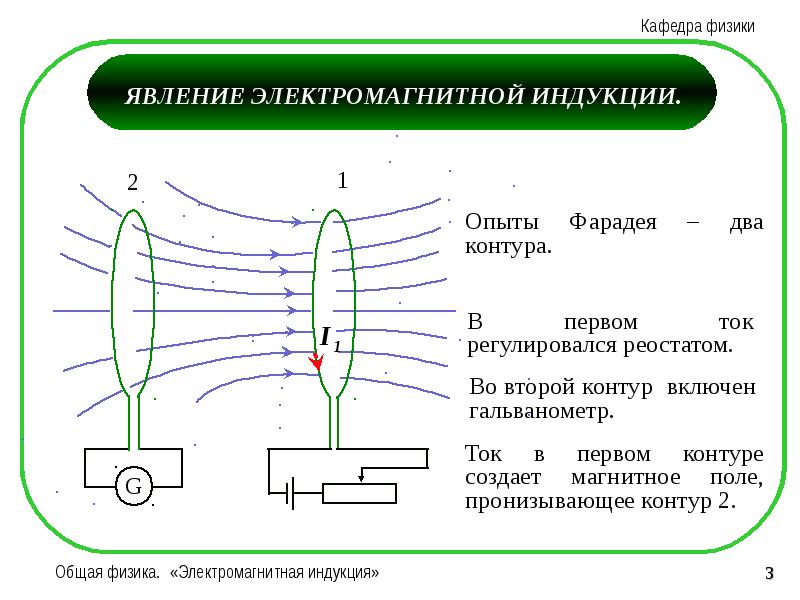 В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке.Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по устройству записывающей головке.Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в катушке провода в головке воспроизведения. Затем этот сигнал отправляется на громкоговоритель или видеоплеер.
Рисунок 6.8 Головки записи и воспроизведения, используемые с аудио- и видеомагнитофонами. (Стив Юрветсон)
Аналогичные принципы применимы и к жестким дискам компьютеров, но с гораздо большей скоростью. Здесь записи на вращающемся диске с покрытием. Считывающие головки исторически заставляли работать по принципу индукции.Однако входная информация передается в цифровой, а не в аналоговой форме — на вращающемся жестком диске записывается последовательность нулей или единиц. Сегодня большинство считывающих устройств с жестких дисков не работают по принципу индукции, а используют технику, известную как гигантское магнитосопротивление — открытие, что слабые изменения магнитного поля в тонкой пленке железа и хрома могут вызвать гораздо большие изменения в электрическое сопротивление было одним из первых крупных успехов нанотехнологии. Еще одно применение индукции можно найти на магнитной полосе на обратной стороне вашей личной кредитной карты, используемой в продуктовом магазине или банкомате.Это работает по тому же принципу, что и аудио- или видеокассета, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.
Еще одно применение индукции можно найти на магнитной полосе на обратной стороне вашей личной кредитной карты, используемой в продуктовом магазине или банкомате.Это работает по тому же принципу, что и аудио- или видеокассета, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.
Еще одним применением электромагнитной индукции является передача электрических сигналов через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном снаружи черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе.Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы необходимо передавать через различные среды.
Рис. 6.9 Электромагнитная индукция, используемая для передачи электрических токов через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (Бьорн Кнетч)
(Бьорн Кнетч)
Еще одной современной областью исследований, в которой электромагнитная индукция успешно реализуется со значительным потенциалом, является транскраниальная магнитная стимуляция.При транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в мозге. В выявленных местах индуцируются слабые электрические токи, что может привести к восстановлению электрических функций в тканях головного мозга.
Апноэ во сне ( остановка дыхания ) поражает как взрослых, так и младенцев, особенно недоношенных детей, и может быть причиной внезапной детской смерти (ВСН). У таких людей дыхание может неоднократно останавливаться во время сна.Прекращение более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль.В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Беспокойство у младенцев вызывает остановка дыхания на эти более длительные периоды времени. Один из типов мониторов для оповещения родителей о том, что ребенок не дышит, использует электромагнитную индукцию. Через провод, обернутый вокруг грудной клетки младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца, когда он дышит, изменяет площадь, проходящую через спираль.В расположенной рядом съемной катушке индуцируется переменный ток, обусловленный изменяющимся магнитным полем исходного провода. Если ребенок перестанет дышать, индуцированный ток изменится, и родитель может быть предупрежден.
Установление связей: сохранение энергии
Закон Ленца является проявлением закона сохранения энергии. ЭДС индукции создает ток, противодействующий изменению потока, потому что изменение потока означает изменение энергии. Энергия может войти или уйти, но не мгновенно.Закон Ленца является следствием. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
На самом деле, если бы ЭДС индукции была направлена в том же направлении, что и изменение потока, существовала бы положительная обратная связь, которая давала бы нам свободную энергию без видимого источника — закон сохранения энергии был бы нарушен.
Пример 6.1 Расчет ЭДС: насколько велика ЭДС индукции?
Рассчитайте величину ЭДС индукции, когда магнит на рис. 6.7 (а) вталкивается в катушку, учитывая следующую информацию: катушка с одним контуром имеет радиус 6.00 см, а среднее значение BcosθBcosθ размером 12{B»cos»θ} {} (данное, поскольку поле стержневого магнита комплексное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.
Стратегия
Чтобы найти величину ЭДС, мы используем закон индукции Фарадея, сформулированный как ЭДС=-NΔΦΔt, ЭДС=-NΔΦΔt, но без знака минус, указывающего направление.
6.3 ЭДС=NΔΦΔtэмс=NΔΦΔt
Раствор
Нам дано, что N=1N=1 размер 12{N=1} {} и Δt=0. 100 с, Δt=0,100 с, но мы должны определить изменение потока ΔΦΔΦ размером 12{ΔΦ} {}, прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
100 с, Δt=0,100 с, но мы должны определить изменение потока ΔΦΔΦ размером 12{ΔΦ} {}, прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что
6.4 ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ).ΔΦ=Δ(BAcosθ)=AΔ(Bcosθ). размер 12{ΔΦ=Δ \( BA»cos»θ \) =AΔ \( B»cos»θ \) } {}
Теперь Δ(Bcosθ)=0,200 Тл, Δ(Bcosθ)=0,200 Тл, размер 12{Δ \( B»cos»θ \)=0 «.» «200»`T} {}, так как было задано, что BcosθBcosθ размер 12{B»cos»θ} {} изменяется от 0,0500 до 0,250 Тл. Площадь петли A=πr2=(3,14…)(0,060 м)2=1,13×10-2м2.A=πr2=(3,14…)(0,060 м)2=1,13×10-2 м2. size 12{A=πr rSup { size 8{2} } = \( 3 «.» «14» «.» «.» «.» \) \( 0 «.» «060»`m \) rSup { размер 8{2} } =1 «.» «13» умножить на «10» rSup { size 8{ — 2} } `m rSup { size 8{2} } } {} Таким образом,
6,5 ΔΦ=(1,13×10–2 м2)(0,200 Тл).ΔΦ=(1,13×10–2 м2)(0,200 Тл). размер 12{ΔΦ= \( 1 «.» «13» умножить на «10» rSup { размер 8{ — 2} } «m» rSup { размер 8{2} } \) \( 0 «.» «200»» Т» \) } {}
Ввод найденных значений в выражение для ЭДС дает
6. 6 ЭДС=NΔΦΔt=(1.13×10-2 м2)(0,200Тл)0,100с=22,6мВ.Эдс=NΔΦΔt=(1,13×10-2 м2)(0,200Тл)0,100с=22,6мВ. размер 12{E=N {{ΔΦ} над {Δt} } = { { \( 1 «.» «13» умножить на «10» rSup {размер 8{- 2} } «m» rSup {размер 8{2} } \) \( 0 «.» «200»» T» \) } более {0 «.» «100»» с»} } =»22″ «.» 6″ мВ»} {}
6 ЭДС=NΔΦΔt=(1.13×10-2 м2)(0,200Тл)0,100с=22,6мВ.Эдс=NΔΦΔt=(1,13×10-2 м2)(0,200Тл)0,100с=22,6мВ. размер 12{E=N {{ΔΦ} над {Δt} } = { { \( 1 «.» «13» умножить на «10» rSup {размер 8{- 2} } «m» rSup {размер 8{2} } \) \( 0 «.» «200»» T» \) } более {0 «.» «100»» с»} } =»22″ «.» 6″ мВ»} {}
Обсуждение
Хотя это легко измеряемое напряжение, оно явно недостаточно велико для большинства практических применений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.
Эксперимент 1 — Магнитные поля катушек и закон Фарадея
АППАРАТЫ
На рисунках ниже:
- Стенд с датчиком магнитного поля, стойкой линейного перемещения и датчиком вращательного движения
- Прокладка для установки датчика магнитного поля на принадлежность для линейного перемещения
- Катушки Гельмгольца
- Две поисковые катушки с параллельными резисторами 10 кОм
Не показано на рисунках выше:
- Компьютер и интерфейс
- Датчик напряжения
- Блок питания постоянного тока до 2 А
- Мультиметр Fluke
- Угломер EZ
ПРИМЕЧАНИЕ ДЛЯ ИНСТРУКТОРОВ
Этот эксперимент состоит из двух частей.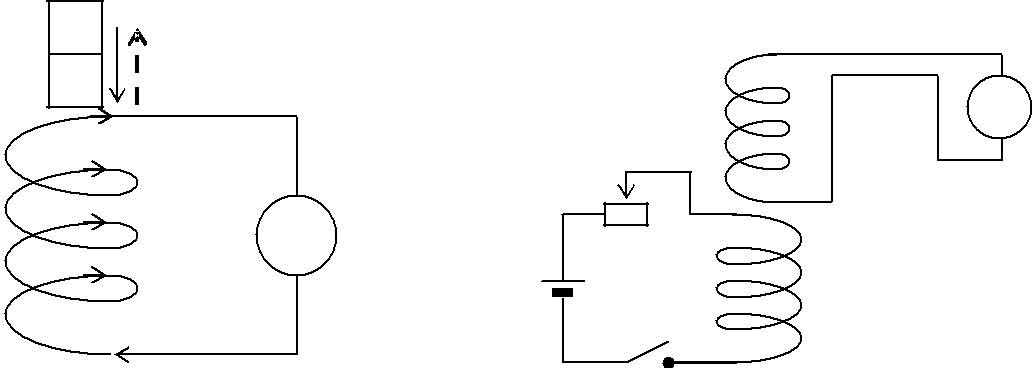 Часть 1 включает проверку магнитного поля, создаваемого токовой петлей, а часть 2 представляет собой исследование закона Фарадея. Большинство студентов не могут выполнить эти две части за одно лабораторное занятие, поэтому вам следует выбрать, какую часть они вам больше всего нравятся. Вариант по умолчанию (в котором вы не выражаете предпочтения) — часть 2.
Часть 1 включает проверку магнитного поля, создаваемого токовой петлей, а часть 2 представляет собой исследование закона Фарадея. Большинство студентов не могут выполнить эти две части за одно лабораторное занятие, поэтому вам следует выбрать, какую часть они вам больше всего нравятся. Вариант по умолчанию (в котором вы не выражаете предпочтения) — часть 2.
МАГНИТНЫЕ ПОЛЯ
Самый основной принцип электричества и магнетизма заключается в том, что заряды воздействуют на другие заряды. Эта картина очень проста, если заряды неподвижны: присутствует только кулоновская сила.Однако вместо того, чтобы описывать силы как действие на расстоянии, мы будем использовать картину поля, согласно которой один заряд создает поле, а другие заряды в поле ощущают силы поля. Если заряды стационарны, то задействованы только электрические поля; но если заряды движутся, в игру вступают и магнитные поля. Полевая картина используется потому, что фундаментальные уравнения электричества и магнетизма — уравнения Максвелла — намного проще, если записать их в терминах полей, чем в терминах сил. 3. \label{eqn_2} \end{eqnarray}
3. \label{eqn_2} \end{eqnarray}
Если пробный заряд неподвижен, то на него действует только электрическая сила \(\textbf{F}_E\):
\begin{eqnarray} \textbf{F}_E &=& q\textbf{E}. \label{eqn_3} \end{eqnarray}
Если пробный заряд движется, то на него также действует магнитная сила \(\textbf{F}_B\):
\begin{eqnarray} \textbf{F}_B &=& q\textbf{v}\times\textbf{B}. \label{eqn_4} \end{eqnarray}
Часто в случае магнитных полей движущиеся заряды являются частью электрического тока.Рассмотрим поток \(i\) зарядов \(q\), движущихся со средней дрейфовой скоростью \(v_0\).
Если число зарядов в единице объема в материале равно \(n\), то суммарный заряд \(\Delta q\) в цилиндрическом объеме с площадью поперечного сечения \(A\) и длиной \(\Delta L = v_0\Delta t\) равно \(nqA\Delta L\), так как объем элемента равен \(A\Delta L\). Таким образом, ток \(i\), проходящий через один колпачок цилиндрического элемента, равен
\begin{eqnarray} i &=& \Delta q/\Delta t = nqA \Delta L / \Delta t = nqA(v_0\Delta t)/\Delta t = nqAv_0. 3.\label{eqn_6} \end{eqnarray}
3.\label{eqn_6} \end{eqnarray}
Уравнение \eqref{eqn_6} — это Закон Био и Савара . (Мы называем магнитное поле этого элемента \(\Delta\textbf{B}\), так как должны быть дополнительные вклады в \(\textbf{B}\) от других частей провода, по которому течет ток.)
МАГНИТНОЕ ПОЛЕ В ЦЕНТРЕ ПРОВОДНОЙ ПЕТЛИ
Рассмотрим круглую проволочную петлю радиуса \(R\), по которой течет ток \(i\). Нас интересует магнитное поле в центре провода.(Конечно, реальная петля в какой-то момент должна быть разорвана батареей, чтобы ток продолжал течь через сопротивление провода, если только провод не является сверхпроводником.)
.
Для текущего цикла векторное произведение \(\Delta\textbf{L} \times \textbf{r}\) перпендикулярно плоскости цикла, поэтому все \(\Delta\textbf{L}\) члены вносят вклад в магнитное поле в том же направлении. Обратите внимание, что в этом случае величина \(\textbf{r}\) (вектор от текущего элемента до точки наблюдения) равна \(R\) (радиус петли). 3 = (\mu_0/4\pi) (2\pi i/R), \label{eqn_7} \end{eqnarray}
3 = (\mu_0/4\pi) (2\pi i/R), \label{eqn_7} \end{eqnarray}
, а направление \(\textbf{B}\) перпендикулярно плоскости петли. Если вы согните пальцы правой руки в направлении, в котором течет ток (который, по соглашению, положительный), то ваш большой палец будет указывать в направлении \(\textbf{B}\).
Для контура из \(N\) витков ток в \(N\) раз превышает ток в одном витке, поэтому величина \(\textbf{B}\) будет равна
\begin{eqnarray} B &=& (\mu_0/4\pi) (2\pi Ni/R).{1/2}\). Вклад магнитного поля \(\textrm{d}\textbf{B}\) находится под углом \(\theta\) по отношению к оси \(z\). Когда мы интегрируем по кругу, складываются только вертикальные (\(\cos\theta\)) компоненты; горизонтальные (\(\sin\theta\)) компоненты компенсируются равным вкладом на противоположной стороне. Также обратите внимание, что угол \(\альфа\) равен \(\тета\), из теоремы геометрии, что если две линии встречаются под углом, то две другие линии, каждая из которых перпендикулярна одной из первых двух линий, составляют тот же угол. {3/2}]. \label{eqn_9} \end{eqnarray}
{3/2}]. \label{eqn_9} \end{eqnarray}
Вы должны быть в состоянии быстро проверить, что уравнение. \eqref{eqn_9} сводится к уравнению. \eqref{eqn_8} для \(B\) в \(z = 0\).
ЗАКОН ФАРАДЕЯ
Концептуально закон Фарадея говорит нам, что изменение магнитных полей индуцирует электрические поля. Математически этот закон гласит, что ЭДС \(\mathcal{E}\) — интеграл электрического поля вокруг замкнутого пути — равен изменению магнитного потока \(\Phi\) через путь:
\begin{eqnarray} \mathcal{E} &=& \int \textbf{E}\cdot\textrm{d}\textbf{l} = -\textrm{d}\Phi/\textrm{d}t, \label{eqn_10} \end{eqnarray}
где
\begin{eqnarray} \Phi &=& \int \textbf{B}\cdot\textrm{d}\textbf{A} \end{eqnarray}
Знак минус в уравнении.\eqref{eqn_10} напоминает нам о законе Ленца: ЭДС индуцируется в таком направлении, чтобы противодействовать изменению магнитного потока, вызвавшему ее.
В этом эксперименте мы будем проверять закон Фарадея, наблюдая за ЭДС, наведенной в небольшой поисковой катушке из \(N\) витков, расположенной в изменяющемся магнитном поле. Для такой катушки ЭДС будет в \(N\) раз больше, чем ЭДС индукции за один виток:
Для такой катушки ЭДС будет в \(N\) раз больше, чем ЭДС индукции за один виток:
\begin{eqnarray} \mathcal{E} &=& -N\,\textrm{d}\Phi/\textrm{d}t.\end{eqnarray}
Кроме того, если поисковая катушка достаточно мала, так что \(\textbf{B}\) можно считать постоянной по площади, то
\begin{eqnarray} \Phi &=& \int \textbf{B}\cdot\textrm{d}\textbf{A} = \textbf{B}\cdot \int\textrm{d}\textbf{A} = \textbf{B}\cdot\textbf{A}. \end{eqnarray}
Объединяя эти результаты, мы получаем вариант закона Фарадея, который будет проверяться в этом эксперименте:
\begin{eqnarray} \mathcal{E} &=& -(\textrm{d}/\textrm{d}t) (\textbf{B} \cdot N\textbf{A}).\label{eqn_11} \end{eqnarray}
ЭДС \(\mathcal{E} = \int \textbf{E}\cdot\textrm{d}\textbf{l}\) очень похожа на разность потенциалов \(\Delta V = \int \textbf{ E}\cdot\textrm{d}\textbf{l}\), и может быть измерена вольтметром или датчиком напряжения Data Studio.
ПРОЦЕДУРА ПРОВЕРКИ МАГНИТНОГО ПОЛЯ ТОКОВОЙ КОНТУРА
Мы будем использовать датчик вращательного движения с аксессуаром линейного движения для отображения осевого поля катушки с током.
 Расположите свой аппарат, как показано на схеме ниже. Мы не используем вторую катушку до шага 8. Она может присутствовать, но пока не должна быть подключена к источнику питания.
Расположите свой аппарат, как показано на схеме ниже. Мы не используем вторую катушку до шага 8. Она может присутствовать, но пока не должна быть подключена к источнику питания.Дважды щелкните датчик вращательного движения в Data Studio и вставьте его разъемы в соответствующие цифровые каналы. Также вызовите датчик магнитного поля в окне настройки и вставьте физический штекер в аналоговый канал A.
При измерении магнитного поля катушка получает питание от источника постоянного тока, который подключается через мультиметр Fluke для измерения тока в катушке. Обязательно установите грубый и точный регуляторы напряжения источника питания на ноль перед включением источника питания; в противном случае начальный ток может быть слишком большим и перегореть предохранитель в мультиметре. Для измерения тока мультиметр должен быть подключен последовательно к источнику питания. Подключите один провод от земли источника питания постоянного тока к «общему» разъему мультиметра.
 Подключите второй провод от разъема мА мультиметра к одному из разъемов катушки. Штекер второй катушки подключается обратно к другому выходному штекеру источника питания.Провод напрямую к выводам катушки; не используйте встроенный последовательный резистор 1,2 кОм в этой части эксперимента. Настройте мультиметр на показания по шкале постоянного тока 2000 мА.
Подключите второй провод от разъема мА мультиметра к одному из разъемов катушки. Штекер второй катушки подключается обратно к другому выходному штекеру источника питания.Провод напрямую к выводам катушки; не используйте встроенный последовательный резистор 1,2 кОм в этой части эксперимента. Настройте мультиметр на показания по шкале постоянного тока 2000 мА.Установите регулятор напряжения источника питания на ноль, включите источник питания и медленно регулируйте грубый и точный регуляторы напряжения, пока не получите ток 1000 мА = 1 А.
Произвести предварительную проверку магнитного поля катушки. Аккуратно расположите конец датчика магнитного поля в центре катушки.(Мы еще не используем датчик вращения на компьютере.) Используйте элементы управления на датчике магнитного поля (аппаратное обеспечение), чтобы установить его в радиальный режим и 10-кратное показание. Дважды щелкните датчик магнитного поля на экране компьютера и убедитесь, что 10-кратное измерение отображается в столбце «Данные».
 Перетащите окно цифр на датчик магнитного поля и перетащите на него данные 10×. Выключите подачу тока на катушку от источника питания и нажмите «Старт», чтобы увидеть показания датчика в гауссах. Нажмите кнопку «Тара» на датчике, чтобы обнулить показания магнитного поля.Рекомендуется всегда обнулять датчик магнитного поля при нулевом токе перед записью измерений при включенном токе. Даже при обнулении показания могут немного прыгать. Теперь снова включите источник питания и запишите показания магнитного поля и тока. (Если ваши измерения магнитного поля имеют отрицательные значения и вам это не нравится, поменяйте местами провода к источнику питания.)
Перетащите окно цифр на датчик магнитного поля и перетащите на него данные 10×. Выключите подачу тока на катушку от источника питания и нажмите «Старт», чтобы увидеть показания датчика в гауссах. Нажмите кнопку «Тара» на датчике, чтобы обнулить показания магнитного поля.Рекомендуется всегда обнулять датчик магнитного поля при нулевом токе перед записью измерений при включенном токе. Даже при обнулении показания могут немного прыгать. Теперь снова включите источник питания и запишите показания магнитного поля и тока. (Если ваши измерения магнитного поля имеют отрицательные значения и вам это не нравится, поменяйте местами провода к источнику питания.)Магнитное поле (Гаусс) =
Ток (мА) =
Сравните измеренное магнитное поле с расчетным полем из \(B = (\mu_0/4\pi) (2\pi Ni/R)\) (уравнение.\eqref{eqn_8}). Помните, что \(\mu_0/4\pi\) = 10 -7 Tm/A, и вы можете прочитать значение \(N\) (количество витков) и \(R\) (радиус катушки).
 Убедитесь, что \(R\) и \(i\) указаны в правильных единицах СИ. Эта формула дает \(B\) в теслах; преобразовать в гаусс, используя 1 тесла = 10 4 гаусс.
Убедитесь, что \(R\) и \(i\) указаны в правильных единицах СИ. Эта формула дает \(B\) в теслах; преобразовать в гаусс, используя 1 тесла = 10 4 гаусс.Расчетное магнитное поле (Гаусс) =
Ошибка в процентах =
Теперь расположите подставку с датчиком магнитного поля, чтобы отобразить магнитное поле катушки вдоль ее оси.Ваше расположение должно быть таким, чтобы при повороте датчика вращательного движения датчик магнитного поля начинался с одной стороны катушки, проходил через центр катушки и перемещался за другую сторону, всегда оставаясь на оси катушки. Дважды щелкните значок датчика вращения и проверьте измерение положения, чтобы оно отображалось в столбце «Данные». На экране компьютера перетащите график на датчик вращательного движения. Перетащите данные о положении на ось \(x\) графика, а данные о магнитном поле — на ось \(y\).
 Сделайте пробный запуск, отключив ток, обнулив показания магнитного поля кнопкой «Тара», включив ток, нажав «Старт» и перемещая датчик по полю, вращая шкив на датчике вращательного движения. Вращайте плавно — хотя скорость не важна, так как мы ничего не строим как функцию времени. Вы должны увидеть хороший график зависимости магнитного поля от осевого расстояния.
Сделайте пробный запуск, отключив ток, обнулив показания магнитного поля кнопкой «Тара», включив ток, нажав «Старт» и перемещая датчик по полю, вращая шкив на датчике вращательного движения. Вращайте плавно — хотя скорость не важна, так как мы ничего не строим как функцию времени. Вы должны увидеть хороший график зависимости магнитного поля от осевого расстояния.После всех доработок, когда у вас на компьютере будет красивый сюжет, вы можете его распечатать.НЕ СТИРАТЬ ДАННЫЕ. Сохраните его в файле, который вы можете получить на рабочем столе. Вы можете использовать его позже для получения дополнительных кредитов.
Теперь подключите вторую катушку параллельно первой. Вы хотите, чтобы токи в катушках протекали в одном направлении, поэтому магнитные поля двух катушек складываются в пространстве между катушками. Снова отрегулируйте напряжение источника питания так, чтобы ток каждой катушки составлял 1 А (при общем токе 2 А). Расположите подставку с датчиком магнитного поля так, чтобы она двигалась вдоль оси обеих катушек, особенно охватывая область между ними.
 Проведите три измерения \(B\) в зависимости от осевого расстояния с расстояниями между катушками, равными \(0,5 R\), \(1,0 R\) и \(1,5 R\), где \(R\) — радиус катушки. (Чтобы сделать три графика сопоставимыми, начинайте каждое измерение с конца датчика магнитного поля в центре одной катушки. Если выводы второй катушки мешают вам переместить ее на расстояние \(0,5 R\) от первая катушка, как вы можете манипулировать прибором, чтобы сделать это измерение возможным?) Расположите график на компьютере так, чтобы все три графика отображались на одном графике по вертикали.Вы можете распечатать эту страницу для своих записей.
Проведите три измерения \(B\) в зависимости от осевого расстояния с расстояниями между катушками, равными \(0,5 R\), \(1,0 R\) и \(1,5 R\), где \(R\) — радиус катушки. (Чтобы сделать три графика сопоставимыми, начинайте каждое измерение с конца датчика магнитного поля в центре одной катушки. Если выводы второй катушки мешают вам переместить ее на расстояние \(0,5 R\) от первая катушка, как вы можете манипулировать прибором, чтобы сделать это измерение возможным?) Расположите график на компьютере так, чтобы все три графика отображались на одном графике по вертикали.Вы можете распечатать эту страницу для своих записей.Какое разделение катушек создает наиболее однородное магнитное поле между катушками?
Это устройство называется катушками Гельмгольца и представляет собой метод создания относительно постоянного контролируемого магнитного поля на значительном пространстве.
 Конечно, мы только что измерили магнитное поле вдоль оси, но поле достаточно однородно на протяжении большей части объема пространства между катушками.Мы использовали это свойство катушек Гельмгольца в предыдущем эксперименте \(e/m\).
Конечно, мы только что измерили магнитное поле вдоль оси, но поле достаточно однородно на протяжении большей части объема пространства между катушками.Мы использовали это свойство катушек Гельмгольца в предыдущем эксперименте \(e/m\).
ПРОЦЕДУРА — ЗАКОН ФАРАДЕЯ
Отключите и отложите блок питания, мультиметр и подставку с датчиком магнитного поля. Начните с нового отображения в Студии данных, обязательно сохранив данные, которые могут понадобиться для дополнительного кредита.
Подключите выход генератора сигналов интерфейса Научной мастерской к одной из катушек, включая 1.Резистор 2 кОм последовательно. Мы будем называть это «катушка поля». Поскольку сопротивление самой катушки пренебрежимо мало по сравнению с 1,2 кОм резистора, напряжение генератора сигналов, деленное на 1,2 кОм, дает ток через катушку возбуждения.
Подключите датчик напряжения (просто аналоговый штекер с двумя проводами) к поисковой катушке на 2000 витков и настройте его в Data Studio.
 Поисковые катушки имеют параллельно резисторы 10 кОм для гашения колебаний. На экране компьютера дважды щелкните «Signal Output», чтобы вывести выходное напряжение в столбец данных и открыть окно управления генератором сигналов.Настройте дисплей осциллографа с двумя трассами для измерения как выходного напряжения генератора сигналов, так и выходного сигнала датчика напряжения. Выберите напряжение генератора сигналов, чтобы осциллограф срабатывал по этому сигналу.
Поисковые катушки имеют параллельно резисторы 10 кОм для гашения колебаний. На экране компьютера дважды щелкните «Signal Output», чтобы вывести выходное напряжение в столбец данных и открыть окно управления генератором сигналов.Настройте дисплей осциллографа с двумя трассами для измерения как выходного напряжения генератора сигналов, так и выходного сигнала датчика напряжения. Выберите напряжение генератора сигналов, чтобы осциллограф срабатывал по этому сигналу.Настройте генератор сигналов на треугольную волну 5 В с частотой 2000 Гц, включите его, нажмите «Пуск» и внесите любые изменения в осциллограф, чтобы на осциллографе отображалась четкая и стабильная треугольная волна. Проверьте настройку триггера, если волна на прицеле нестабильна.Отрегулируйте скорость следа, нажимая стрелки на оси \(x\) осциллографа, и амплитуду следа, нажимая соответствующие стрелки на оси \(y\). Теперь, когда вы поместите поисковую катушку внутрь катушки возбуждения и в той же плоскости и отрегулируете сигнал датчика напряжения на осциллографе до большей чувствительности, вы должны увидеть след прямоугольной формы, возможно, с некоторыми колебаниями.
 Обратите внимание, что когда вы нажимаете «Стоп», последняя трасса осциллографа остается фиксированной в окне осциллографа, что облегчает выполнение некоторых из приведенных ниже измерений.
Обратите внимание, что когда вы нажимаете «Стоп», последняя трасса осциллографа остается фиксированной в окне осциллографа, что облегчает выполнение некоторых из приведенных ниже измерений.Закон Фарадея (уравнение \eqref{eqn_11}) утверждает, что \(\mathcal{E} = -(\textrm{d}/\textrm{d}t) (\textbf{B} \cdot N\textbf{A })\), где \(\mathcal{E}\) — ЭДС, наведенная в поисковой катушке (которую вы измеряете датчиком напряжения). \(\textbf{B}\) — магнитное поле катушки возбуждения, пропорциональное протекающему через нее току; этот ток, в свою очередь, пропорционален напряжению треугольной волны от генератора сигналов. \(\textbf{A}\) — вектор площади поисковой катушки, а \(N\) — количество витков поисковой катушки.Косинус скалярного произведения между \(\textbf{B}\) и \(\textbf{A}\) равен 1,0, если поисковая катушка находится в той же плоскости, что и катушка возбуждения.
Изучите две кривые осциллографа и четко, кратко и четко объясните форму и фазу выходного сигнала датчика напряжения, используя приведенное выше уравнение.

ПРОЦЕДУРА — ЗАВИСИМОСТЬ \(\mathcal{E}\) ОТ \(\textrm{d}i/\textrm{d}t\)
Как видно из закона Фарадея, \(\mathcal{E}\) пропорционально \(\textrm{d}i/\textrm{d}t\) (где \(i\) — ток через катушки возбуждения), так как \(B\) катушки возбуждения пропорциональна \(i\).В свою очередь, \(\textrm{d}i/\textrm{d}t\) связано с частотой треугольной волны. Запишите правильное уравнение, связывающее \(\textrm{d}i/\textrm{d}t\) с частотой \(f\) и амплитудой \(i_{\textrm{m}}\) для треугольной волны.
Проверьте это соотношение.
 Измерьте \(\mathcal{E}\) (поместив интеллектуальный инструмент на прямоугольную волну после того, как вы нажмете «Стоп») на частотах 500, 1000, 1500, 2000 и 2500 Гц.Введите свои данные в новый рабочий лист Excel, диаграмму \(\mathcal{E}\) как функцию \(f\) с четким заголовком и метками на осях. Вы можете распечатать график для своих записей. Убедитесь, что вы размещаете поисковую катушку в одном и том же месте в центре катушки возбуждения при каждом измерении.
Измерьте \(\mathcal{E}\) (поместив интеллектуальный инструмент на прямоугольную волну после того, как вы нажмете «Стоп») на частотах 500, 1000, 1500, 2000 и 2500 Гц.Введите свои данные в новый рабочий лист Excel, диаграмму \(\mathcal{E}\) как функцию \(f\) с четким заголовком и метками на осях. Вы можете распечатать график для своих записей. Убедитесь, что вы размещаете поисковую катушку в одном и том же месте в центре катушки возбуждения при каждом измерении.
ЗАВИСИМОСТЬ \(\mathcal{E}\) ОТ СКАЧЕЧНОГО ПРОИЗВЕДЕНИЯ С ВЕКТОРОМ ПЛОЩАДЕЙ
Разработайте способ использования угломера EZ для регулировки угла скалярного произведения в \(\textbf{B} \cdot N\textbf{A}\) между вектором площади поисковой катушки и магнитным полем (перпендикулярно плоскость катушки возбуждения).Поисковая катушка должна находиться в центре катушки возбуждения для каждого измерения. Это может помочь, если оба партнера по лаборатории держат части оборудования.
 Помните, что когда вы нажмете «Стоп», сигнал останется на осциллографе для удобства измерения с помощью интеллектуального инструмента.
Помните, что когда вы нажмете «Стоп», сигнал останется на осциллографе для удобства измерения с помощью интеллектуального инструмента.Сохраняя постоянными частоту и амплитуду треугольной волны, измерьте \(\mathcal{E}\) для углов скалярного произведения 0°, 30°, 45°, 60° и 90°. Запишите свои данные в новый рабочий лист Excel, вычислите косинусы с помощью операции заполнения и нарисуйте график \(\mathcal{E}\) как функцию косинуса угла.Назовите диаграмму и четко обозначьте оси. Вы можете распечатать его для своих записей.
ПРОЦЕДУРА — ЗАВИСИМОСТЬ ОТ \(N\)
До сих пор мы использовали поисковую катушку на 2000 витков. Измерьте \(\mathcal{E}\) с помощью треугольной волны с амплитудой 5 В и частотой 2000 Гц, используя поисковую катушку с 2000 витками в центре катушки возбуждения и в той же плоскости. Теперь, что должно быть \(\mathcal{E}\) с поисковой катушкой на 400 витков? Повторите измерение с катушкой из 400 витков и запишите результат ниже.

Предсказанный \(\mathcal{E}\) с 400 оборотами =
Измерено \(\mathcal{E}\) с 400 витками =
ПРОЦЕДУРА — СИНУСОУС
Если ток в катушке возбуждения представляет собой синусоидальную волну, какую форму волны (включая информацию о фазе) должен принимать индуцированный \(\mathcal{E}\)? Проверьте это на своем оборудовании.
ДОПОЛНИТЕЛЬНЫЙ КРЕДИТ (максимум 5 мельниц)
Прежде чем приступить к дополнительным кредитам, убедитесь, что у вас есть следующие графики с правильными данными, заголовками и помеченными осями:
Магнитное поле в зависимости от осевого расстояния для одной катушки.
На одном графике нанесены три измерения магнитного поля в зависимости от осевого расстояния для трех различных расстояний между катушками.
 {3/2} \справа]. \end{eqnarray}
{3/2} \справа]. \end{eqnarray}Вернитесь к ранее сохраненным данным для магнитного поля вдоль оси катушки. Настройте расчет в Data Studio для приведенного выше уравнения и нанесите его на тот же график, что и данные магнитного поля, чтобы вы могли сравнить теоретическое магнитное поле с измеренным полем. Награда составляет 5 миллионов, если у вас есть аккуратно помеченная распечатка, сделанная без существенной помощи со стороны вашего ТА. Если вам нужна помощь, вы можете «купить» различное количество, отказавшись от некоторых из 5 мельниц.Вот пара подсказок: \(B\) в приведенном выше уравнении выражено в теслах, но измеренное поле выражено в гауссах, поэтому включите преобразование в гаусс в расчет теоретического поля. Вам также потребуется изменить начало оси \(z\) в расчетах, чтобы она соответствовала положению центра катушки для вашего измеренного поля.
.


 В соленоид вдвигается (или выдвигается из него) постоянный магнит. При перемещении магнита фиксируют отклонение стрелки гальванометра, что означает возникновение индукционного тока. При увеличении скорости перемещения магнита по отношению к катушке отклонение стрелки увеличивается. Замена полюсов магнита вызывает изменение направления отклонения стрелки гальванометра. Отметим, что магнит можно оставить неподвижным и перемещать соленоид относительно магнита.
В соленоид вдвигается (или выдвигается из него) постоянный магнит. При перемещении магнита фиксируют отклонение стрелки гальванометра, что означает возникновение индукционного тока. При увеличении скорости перемещения магнита по отношению к катушке отклонение стрелки увеличивается. Замена полюсов магнита вызывает изменение направления отклонения стрелки гальванометра. Отметим, что магнит можно оставить неподвижным и перемещать соленоид относительно магнита.
 Расположите свой аппарат, как показано на схеме ниже. Мы не используем вторую катушку до шага 8. Она может присутствовать, но пока не должна быть подключена к источнику питания.
Расположите свой аппарат, как показано на схеме ниже. Мы не используем вторую катушку до шага 8. Она может присутствовать, но пока не должна быть подключена к источнику питания. Подключите второй провод от разъема мА мультиметра к одному из разъемов катушки. Штекер второй катушки подключается обратно к другому выходному штекеру источника питания.Провод напрямую к выводам катушки; не используйте встроенный последовательный резистор 1,2 кОм в этой части эксперимента. Настройте мультиметр на показания по шкале постоянного тока 2000 мА.
Подключите второй провод от разъема мА мультиметра к одному из разъемов катушки. Штекер второй катушки подключается обратно к другому выходному штекеру источника питания.Провод напрямую к выводам катушки; не используйте встроенный последовательный резистор 1,2 кОм в этой части эксперимента. Настройте мультиметр на показания по шкале постоянного тока 2000 мА. Перетащите окно цифр на датчик магнитного поля и перетащите на него данные 10×. Выключите подачу тока на катушку от источника питания и нажмите «Старт», чтобы увидеть показания датчика в гауссах. Нажмите кнопку «Тара» на датчике, чтобы обнулить показания магнитного поля.Рекомендуется всегда обнулять датчик магнитного поля при нулевом токе перед записью измерений при включенном токе. Даже при обнулении показания могут немного прыгать. Теперь снова включите источник питания и запишите показания магнитного поля и тока. (Если ваши измерения магнитного поля имеют отрицательные значения и вам это не нравится, поменяйте местами провода к источнику питания.)
Перетащите окно цифр на датчик магнитного поля и перетащите на него данные 10×. Выключите подачу тока на катушку от источника питания и нажмите «Старт», чтобы увидеть показания датчика в гауссах. Нажмите кнопку «Тара» на датчике, чтобы обнулить показания магнитного поля.Рекомендуется всегда обнулять датчик магнитного поля при нулевом токе перед записью измерений при включенном токе. Даже при обнулении показания могут немного прыгать. Теперь снова включите источник питания и запишите показания магнитного поля и тока. (Если ваши измерения магнитного поля имеют отрицательные значения и вам это не нравится, поменяйте местами провода к источнику питания.) Убедитесь, что \(R\) и \(i\) указаны в правильных единицах СИ. Эта формула дает \(B\) в теслах; преобразовать в гаусс, используя 1 тесла = 10 4 гаусс.
Убедитесь, что \(R\) и \(i\) указаны в правильных единицах СИ. Эта формула дает \(B\) в теслах; преобразовать в гаусс, используя 1 тесла = 10 4 гаусс. Сделайте пробный запуск, отключив ток, обнулив показания магнитного поля кнопкой «Тара», включив ток, нажав «Старт» и перемещая датчик по полю, вращая шкив на датчике вращательного движения. Вращайте плавно — хотя скорость не важна, так как мы ничего не строим как функцию времени. Вы должны увидеть хороший график зависимости магнитного поля от осевого расстояния.
Сделайте пробный запуск, отключив ток, обнулив показания магнитного поля кнопкой «Тара», включив ток, нажав «Старт» и перемещая датчик по полю, вращая шкив на датчике вращательного движения. Вращайте плавно — хотя скорость не важна, так как мы ничего не строим как функцию времени. Вы должны увидеть хороший график зависимости магнитного поля от осевого расстояния. Проведите три измерения \(B\) в зависимости от осевого расстояния с расстояниями между катушками, равными \(0,5 R\), \(1,0 R\) и \(1,5 R\), где \(R\) — радиус катушки. (Чтобы сделать три графика сопоставимыми, начинайте каждое измерение с конца датчика магнитного поля в центре одной катушки. Если выводы второй катушки мешают вам переместить ее на расстояние \(0,5 R\) от первая катушка, как вы можете манипулировать прибором, чтобы сделать это измерение возможным?) Расположите график на компьютере так, чтобы все три графика отображались на одном графике по вертикали.Вы можете распечатать эту страницу для своих записей.
Проведите три измерения \(B\) в зависимости от осевого расстояния с расстояниями между катушками, равными \(0,5 R\), \(1,0 R\) и \(1,5 R\), где \(R\) — радиус катушки. (Чтобы сделать три графика сопоставимыми, начинайте каждое измерение с конца датчика магнитного поля в центре одной катушки. Если выводы второй катушки мешают вам переместить ее на расстояние \(0,5 R\) от первая катушка, как вы можете манипулировать прибором, чтобы сделать это измерение возможным?) Расположите график на компьютере так, чтобы все три графика отображались на одном графике по вертикали.Вы можете распечатать эту страницу для своих записей. Конечно, мы только что измерили магнитное поле вдоль оси, но поле достаточно однородно на протяжении большей части объема пространства между катушками.Мы использовали это свойство катушек Гельмгольца в предыдущем эксперименте \(e/m\).
Конечно, мы только что измерили магнитное поле вдоль оси, но поле достаточно однородно на протяжении большей части объема пространства между катушками.Мы использовали это свойство катушек Гельмгольца в предыдущем эксперименте \(e/m\). Поисковые катушки имеют параллельно резисторы 10 кОм для гашения колебаний. На экране компьютера дважды щелкните «Signal Output», чтобы вывести выходное напряжение в столбец данных и открыть окно управления генератором сигналов.Настройте дисплей осциллографа с двумя трассами для измерения как выходного напряжения генератора сигналов, так и выходного сигнала датчика напряжения. Выберите напряжение генератора сигналов, чтобы осциллограф срабатывал по этому сигналу.
Поисковые катушки имеют параллельно резисторы 10 кОм для гашения колебаний. На экране компьютера дважды щелкните «Signal Output», чтобы вывести выходное напряжение в столбец данных и открыть окно управления генератором сигналов.Настройте дисплей осциллографа с двумя трассами для измерения как выходного напряжения генератора сигналов, так и выходного сигнала датчика напряжения. Выберите напряжение генератора сигналов, чтобы осциллограф срабатывал по этому сигналу. Обратите внимание, что когда вы нажимаете «Стоп», последняя трасса осциллографа остается фиксированной в окне осциллографа, что облегчает выполнение некоторых из приведенных ниже измерений.
Обратите внимание, что когда вы нажимаете «Стоп», последняя трасса осциллографа остается фиксированной в окне осциллографа, что облегчает выполнение некоторых из приведенных ниже измерений.
 Измерьте \(\mathcal{E}\) (поместив интеллектуальный инструмент на прямоугольную волну после того, как вы нажмете «Стоп») на частотах 500, 1000, 1500, 2000 и 2500 Гц.Введите свои данные в новый рабочий лист Excel, диаграмму \(\mathcal{E}\) как функцию \(f\) с четким заголовком и метками на осях. Вы можете распечатать график для своих записей. Убедитесь, что вы размещаете поисковую катушку в одном и том же месте в центре катушки возбуждения при каждом измерении.
Измерьте \(\mathcal{E}\) (поместив интеллектуальный инструмент на прямоугольную волну после того, как вы нажмете «Стоп») на частотах 500, 1000, 1500, 2000 и 2500 Гц.Введите свои данные в новый рабочий лист Excel, диаграмму \(\mathcal{E}\) как функцию \(f\) с четким заголовком и метками на осях. Вы можете распечатать график для своих записей. Убедитесь, что вы размещаете поисковую катушку в одном и том же месте в центре катушки возбуждения при каждом измерении. Помните, что когда вы нажмете «Стоп», сигнал останется на осциллографе для удобства измерения с помощью интеллектуального инструмента.
Помните, что когда вы нажмете «Стоп», сигнал останется на осциллографе для удобства измерения с помощью интеллектуального инструмента.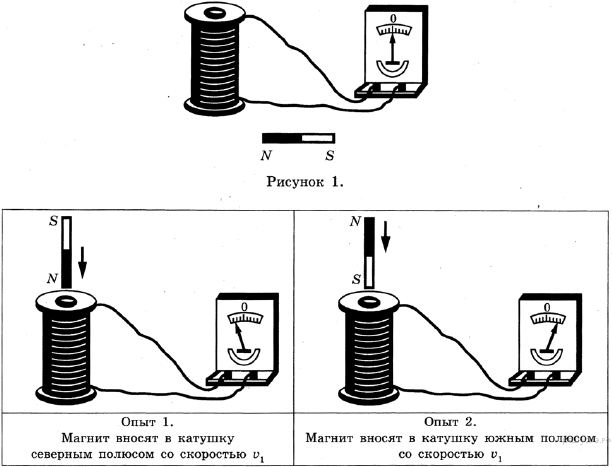
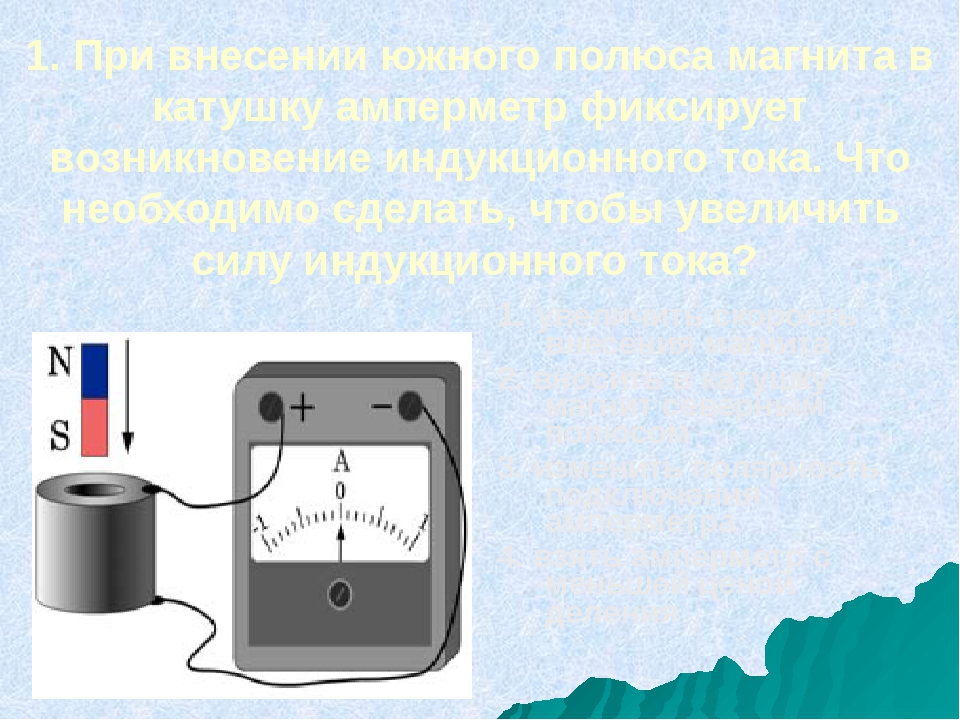 {3/2} \справа]. \end{eqnarray}
{3/2} \справа]. \end{eqnarray}